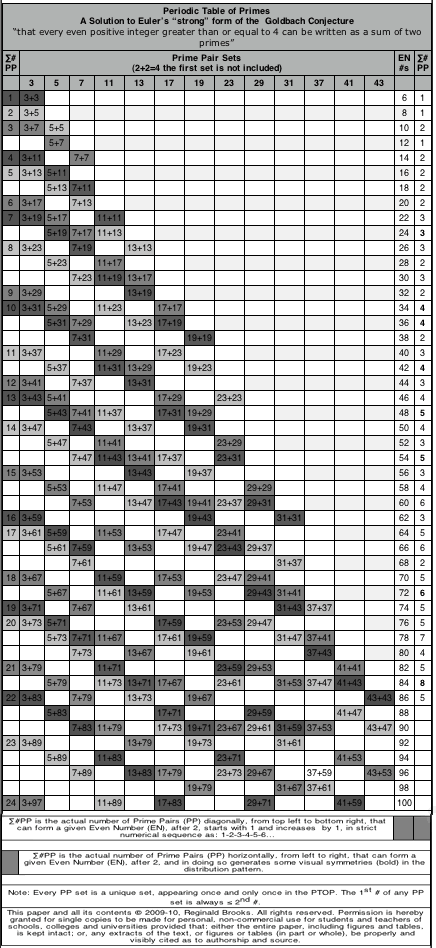
Rule 169: Periodic Table of Primes.
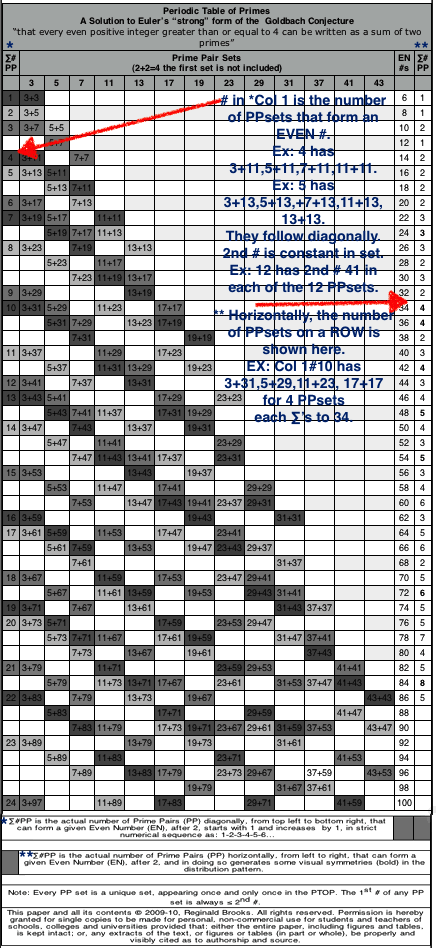
Rule 169: annotated
 Rule 170: Periodic Table of Primes (PTOP): embedded within Brooks (Base) Square.
Rule 170: Periodic Table of Primes (PTOP): embedded within Brooks (Base) Square.
 Rule 170: annotated
Rule 170: annotated


Here’s the thing. Amongst a myriad of other connections, there exists an intimate connection between three number systems on the BBS-ISL Matrix (BIM):
1 The Inverse Square Law (ISL) as laid out in the BIM;
2 PTs — and most especially PPTs — as laid out on the BIM;
3 The PRIME numbers — PRIMES — as laid out on the BIM.
The BIM is the FIXED GRID numerical array of the ISL.
PTs are the Pythagorean Triples and PPTs are the Primitive Pythagorean Triples. They have been extensively covered in the TPISC (The Pythagorean-Inverse Square Connection) series as: TPISC I Basics, TPISC II Advanced, TPISC III Clarity, TPISC IV Details. (See links at bottom.)
The PRIMES vs NO-PRIMES (2019) was covered earlier.
The original MathspeedST (2009-14) work, Brooks (Base) Square (2009-11), that started this journey, was divided in to two sections:
I. TAOST (The Architecture Of SpaceTime);
II. TCAOP (The Conspicuous Absence Of PRIMES).
You see, other than the natural whole numbers that form the BIM Axis’ and the standard 1st Parallel Diagonal (containing ALL the ODDs (≥3), there are NO PRIMES on the BIM.
This is the basis of the PRIMES vs NO-PRIMES work.
Yet, convert that same 1st Parallel Diagonal to ALL EVENS (≥4, by adding 1 to each former ODD), and now the BIM reveals the stealthily hidden PRIMES relationship in forming symmetrical pairs of PRIMES that are ALWAYS equal distance (STEPS) from ANY given EVEN # divided by two.
All this occurs on the BIM Axis. The apex of the 90° Right-angled, isosceles triangle so formed lies on a straight line path from the EVEN/2 to the given EVEN # located on that converted 1st Parallel Diagonal. This relationship is geometrically true and easily seen on the BIM.
Extracting those PRIME-Pair sets (PPsets) for each given EVEN forms the basis for the PTOP — Periodic Table Of PRIMES.
While “hidden” on the BIM, it clearly forms a definitive pattern on the PTOP: for EVERY 3+PRIME PPset that forms the 2nd column on the PTOP — acting like a bifurcation point — a “Trail” of PPsets forms a zig-zagging diagonal pointing down and to the right.
These are ALWAYS — much like a fractal — added with the SAME PRIME Sequence (3,5,7,11,13,17,19,23,29,31,37,...).
When you read a given horizontal line from left to right across the PTOP, you see that each given PPset that was contributed by a PPset Trail, adds up — composes — its respective EVEN. The sum (∑) number of PPsets that form its EVEN is totaled in the last column.
The fractal-like addition of one new, additional PRIME Sequence PPset to each subsequent “Trail” formed results in the overlapping trails growing at a rate that far, far exceeds the growth and incidence of the PRIME Gaps. This ensures that there will always be at least one PPset that will be present to compose ANY EVEN.
The Goldbach Conjecture has been satisfied and a new PRIME pattern has been found.
MathspeedST-TPISC Resource Media Center Intro
MathspeedST-TPISC Resource Media Center
PTOP - Goldbach Conjecture Video
A number of PRIME conjectures have been shown to be easily visualized on the BIM:
Reference: TPISC IV: Details: BIM + PTs + PRIMES
The factors of 24 — 1,24–2,12–3,8–4,6 — when increased or decreased by 1, ultimately pick out ALL ARs. Euler's 6n +/-1 is the most direct, Fermat's 4n + 1 gets the Sums of Two Squares = Pythagorean Primes(while 4n + 3 gets the rest).
Fermat's Little Theorem (as opposed to the more familiar "Fermat's Last Theorem") tests for primality.
But now there is a dead simple way to test for primality:
The difference in the squares between ANY 2 PRIMES (≧5) ALWAYS = n24.
For example, take any random ODD # - 25 —> it must be ÷24 n times to be PRIME. (n=1,2,3,...)
741
7412-52/24 = n= 22877.3 NOT PRIME
189
1892-52/24 = n = 1487.3 NOT PRIME
289
2892-52/24 = n = 3479 PRIME
I would be remiss if I did not mention that throughout this long journey that began with the Inverse Square Law and the Primtive Pythagorean Triples that the PRIMES kinda of just fell out. They just kept popping up. Not the least, but certainly not without effort, the BIM actually directly visualizes ALL of the NO-PRIMES. In doing so, one is left with information that is simply the inverse of the PRIMES. Subtract the NO-PRIMES information from the list of ODDS (disregarding 2) and what remains are ALL the PRIMES! A simple algebraic expression falls out from that:
NP = 6yx +/- y
letting x=1,2,3,… and y=ODDs 3,5,7,… with the only caveat is that if you don't first eliminate all the ÷3 ODDS, you must include exponentials of 3 (3x) in the NP tally.
In 2009-10, a solution to Euler's "strong" form of the Goldbach Conjecture "that every even positive integer greater than or equal to 4 can be written as a sum of two primes" was presented as the BBS-ISL Matrix Rule 169 and 170. This work generated a Periodic Table of Primes (PTOP) in which Prime Pair Sets (PPsets) that sequentially formed the EVEN numbers were laid out. It is highly patterned table. A recently annotated version is included with the original below. (See above link for details.)
It turned out this PTOP was actually embedded — albeit hidden — within the BIM itself as shown in Rule 170 and here, too, a recently annotated version is included below. (See above link for details.)

Rule 169: Periodic Table of Primes.

Rule 169: annotated
 Rule 170: Periodic Table of Primes (PTOP): embedded within Brooks (Base) Square.
Rule 170: Periodic Table of Primes (PTOP): embedded within Brooks (Base) Square.
 Rule 170: annotated
Rule 170: annotated


For every EVEN # that, when subtracting from it 3 (P1), gives a difference (∆) of another P, a 3-PRIME PPset — designated as “3, P2” or “3 + P2”, the sum (∑) P1 + P2 = EVEN # — a PPset Trail is formed.
The PPset Trail follows a strict Number Pattern Sequence (NPS):
• Periodic Table of PRIMES (PTOP) has Column Headers of the PRIMES Sequence 3,5,7,11,13,17,19,23,….;
• The PPset Trail starts on the PTOP under the PRIME = 3 Column;
• It ONLY starts for EVENs formed from “3 + P2” sets;
• The P2 itself sequentially increases DOWN the Column with the SAME NPS spacing as the PRIMES Sequence — leaving a blank space for each PRIME Gap in the sequence;
• The PPset Trail ALWAYS follows the SAME IDENTICAL NPS as it forms a jagged diagonal from Top Left to Bottom Right;
• The PPset Trail NPS is the SAME PRIMES Sequence 3,5,7,11,13,17,19,23,…, but BEGINS the sequence at that PRIME at which that EVEN # - 3 = that PRIME;
• The PPset Trail NPS going sequentially down the diagonal, will skip the next diagonal space – leave blank – for the PRIME Gaps;
• For those EVENs that are NOT “3 + P2” sets, the remaining Columns of the PRIMES Sequence 5,7,11,13,17,19,23,…. will fill in, picking up on a previous PPset Trail from a smaller EVEN above;
• For those EVENS that are NOT “3 + P2” sets, the PPset Trail NPS remains the SAME and IDENTICAL as the “3 + P2” sets, the ONLY difference is that it starts further down the Trail;
• The diagonal length of the PPset Trail increases by 1 PRIME # for each successive “3 + P2” sets and that ∑# of PPsets is given in the 1st Header Column;
• The # of EVENS Covered (EC) by a given PPset Trail — the Ending EVEN # (Ee) - Starting EVEN # (Es) = EC — is important in establishing further NPS as seen in Tables 38-40.
• The Ee = 2P2 (see Tables 38-40);
• Going horizontally across the PTOP, those PPsets from the various diagonally crossing PPset Trails will add up to the ∑ of PPsets that form that EVEN #, as shown in the last Column;
• While it is difficult to visualize here, or in the Tables 38-40, on the BIM one can readily see that EACH PPset is the base of a 90° R-angled isosceles triangle with its apex pointing to the EVEN #! (See rule170annotated image.)
The combination of two (2) PRIME Sequences, P1 and P2 — bifurcating at the P2 — not only gives one or more PPsets for every EVEN#, it also reveals a starling NEW NPS for the PRIMES: PRIMES + PRIMES generates 90° R-angled isosceles triangles!
With that review of the ongoing work, the full presentation of this work starts below. It will cover everything above plus the NEW work leading to the findings and proof of the Goldbach Conjecture. This will be the basis for the ebook: PTOP: Periodic Table of PRIMES & the Goldbach Conjecture
PTOP Goldbach Conjecture from Reginald Brooks on Vimeo.
PTOP: Periodic Table Of PRIMES & theGoldbach ConjectureINTRODUCTIONSTATEMENT: Layout & EssentialsThere are five sets of data to consider:FINDINGS & PROOFSUMMARY and CONCLUSIONDATA: Images and TablesDATA: Images and TablesREFERENCES
While the (strong) Goldbach Conjecture has been verified up to 4x1018, it remains unproven.
A number of attempts have demonstrated substantial, provocative and often beautiful patterns and graphics, none have proven the conjecture.
Proof of the conjecture must not rely solely on the notion that extension of a pattern to infinity will automatically remain valid.
No, instead, a proof must, in its very nature, reveal something new about the distribution and behavior of PRIMES that it is absolutely inevitable that such pattern extension will automatically remain valid. The proof is in the pudding!
Proof offered herein is just such a proof. It offers very new insights, graphical tables and algebraic geometry visualizations into the distribution and behavior of PRIMES.
In doing so, the Proof of the Euler Strong form of the Goldbach Conjecture becomes a natural outcome of revealing the stealthy hidden Number Pattern Sequence (NPS) of the PRIMES.
Proof of the Goldbach Conjecture (strong form, ≥6)
Natural (n), Whole Integer Numbers (WIN) — 0,1,2,3,…infinity — form horizontal and vertical Axis of a simple matrix grid.
The squares of such WINs — n2=12=1, 22=4, 32=9,…infinity — forms the central Diagonal of said grid — dividing it into two bilaterally symmetric triangular halves.
Every Inner Grid (IG) cell within is simply the difference (∆) between its horizontal and vertical Diagonal intercept values. They extend to infinity. The Diagonal WINs form the base of a 90° R-angled isosceles triangle with said IG cell value at the apex.
Every IG cell within is also the product of two Axis WINs (Either horizontal or vertical, not both), that form the base of a 90° R-angled isosceles triangle with said IG cell value at the apex.
The complete matrix grid extends to infinity and is referred to as the BIM (BBS-ISL Matrix).The BIM forms — and informs — a ubiquitous map (algebraic geometry) to:
The Inverse Square Law (ISL);
The 1st Diagonal that runs parallel to either side of the main Prime Diagonal (PD, not of PRIME numbers, but primary), is composed of the ODD WINs: 1,3,5,…infinity.
If we add +1 to each value, that 1st Diagonal now becomes a sequence of ALL the EVEN WINs (≥4): 4, 6, 8,…infinity. NOTE: this is why the PTOP is hidden, in the normal, base BIM these remain ODDs.
Select ANY EVEN WIN and plot a line straight back to its Axis WIN — that Axis WIN = EVEN/2 = core Axis #.
Upon that same Axis, PRIME Pair sets (PPsets) — whose sum (∑) equals the EVEN WIN (on the 1st Diagonal) — will be found that form the base of 90° R-angled isosceles triangle(s) whose apex lie(s) on that straight line between the EVEN and its 1/2 Axis WINs. PPsets with identical PRIMES = 1/2 Axis value.
The proof that every EVEN WIN has ≥1 PPsets can be seen in the Periodic Table Of PRIMES (PTOP) that stealthily informs the BIM of how each and every EVEN WIN is geometrically related to one or more PPsets.
These PPsets are NOT randomly contributing their ∑s to equal the EVEN WINs, rather they come about as the consequence of a strict NPS: the sequential — combining, linking, concatenation — addition of the PRIMES Sequence (PS) — 3,5,7,11,13,17,19,…—to a base PS — 3,5,7,11,13,17,19,….
The NPS of this addition forms the PTOP: for each vertical PS — the 1st PRIME (P1) remains constant (3), the 2nd PRIME (P2) sequentially advances one (1) PS WIN — is matched diagonally with the 2nd PS, but now the 1st PRIME sequentially advances, while the 2nd PRIME remains constant within a given PPset.
This matching addition of the 2nd PS at the bifurcation point of the common 2nd PRIMES, forms the zig-zag diagonal PPset Trails that are the hallmark of the PTOP.
For every subsequent vertical PPset match, the Trail increases by one (1) PPset.
The rate of such PPset Trail growth far exceeds the PRIME Gap rate.
The zig-zag diagonal PPset Trails combine horizontally on the PTOP to give the ∑# of PPsets whose ∑s = The EVEN WIN.
More than simply proving the Goldbach Conjecture, the PTOP hidden within the BIM reveals a new NPS connection of the PRIMES: PRIMES + PRIMES = 90° R-angle isosceles triangles.
The entire BIM, including the ISL—Pythagorean Triples—and, PRIMES, is based on 90° R-triangles!
Similar to how the grid cell values of the Axis, PD and IG of the Pythagorean Triples reveal additional, intimate connections within the BIM, so too do the PPsets: the 1st PRIME values of each set points to the # of STEPS from the PD that intersects the given EVEN WIN (Axis2), on a straight line path back to its Axis, at the apex where its other PPset member intersects — this is no mere coincidence — and that apex is, of course, the 90° R-angle isosceles triangle that results. For example: EVEN = 24, Axis = 12, PD = 144, # of STEPS from PD towards Axis = 5 for the 5+19 PPset and 7 for the 7+17 PPset, and 11 for the 11+13 PPset that each forms the EVEN 24.
As the bifurcation concatenation of the PS — 3,5,7,11,13,17,19,..— with the same base PS — 3,5,7,11,13,17,19,…— of those EVEN WIN — that when “3” is subtracted, the remainder is a next-in-the-sequence PRIME — remains one of a similar split with the Pythagorean Triples: for every “Primitive” parent PT, there are multiple “Non-Primitive” child PTs and it is the PPTs (Primitive Pythagorean Triples) that ultimately form the inter-connectedness of ALL PTs back to the original PPT — the 3-4-5. With the PRIMES, one raises the question: why are these “EVENS” preselected to be the “parent” EVENS forming the “beginning” or “start” of every PPset Trail with all other EVENS hitching on to that Trail further down the sequence?
Another set of STEPS (S) from the core Axis value , directly on the Axis, identifies each symmetrical pair of a given PPset that forms that given EVEN. These STEPS may by Universally calculated from the EVENS, P1 and P2 values. Examples are given further down.
As every new discovery unlocks many more questions, it follows that the details of the PTOP and BIM visualizations should both satisfy the proof offered and, more importantly, provide provocative data that will advance the field for the next researcher!
BIM (BBS-ISL Matrix): grid visualizations that overview the entire work
PTOP: the actual Table
PTOP: Analysis
Reference
PRIME PPset Trails
The DATA has been grouped in its own section down below. It is highly recommended that you, the reader, preview first — review, thereafter.
~~~~
PTOP: Periodic Table Of PRIMES & theGoldbach ConjectureINTRODUCTIONSTATEMENT: Layout & EssentialsThere are five sets of data to consider:FINDINGS & PROOFSUMMARY and CONCLUSIONDATA: Images and TablesDATA: Images and TablesREFERENCES
The definitive proof depends on demonstrating that the PPset Trails grow and extend to cover the “next” EVENS at a rate that exceeds the Prime Gap rate. PRIMES Sequence, PS is the key.
The PS is well established. How many primes are there?
As every beginning PPset — of 3,P2 — forms from successively increasing the 2nd PRIME by the next number in the PS (3,5,7,11,13,17,…), the Trail formed by bifurcating off from that point increases the total number sum (∑) of PPsets by one, i.e. Trail, Trail+1, (Trail+1)+1, ((Trail+1)+1)+1,…
A necessary, and sufficient, condition is that the Trail lengths — i.e. the total number of PPsets, in their overlapping aggregate, always exceed both the number of PRIMES and their Gaps for any and all numbers.
Specifically from Table 46 and Fig.__, locate a P2 PRIME with a large Gap, e.i. P2= 23, Gap=6.
line#———PRIMES, P2—∑#set/Trail—PRIME Gap—∆Trail-Gap— EVEN:∑#sets—EC——Eending——EVEN, E
| 8 | 23 | 8 | 6 | 2 | 26: 3 | 11 | 46 | 26 |
|---|---|---|---|---|---|---|---|---|
We see that 23 has 8 PPsets in its Trail, it has a Gap of 6 to the next PRIME (for a ∆=2). It’s EVEN=26 and there are 3 PPsets (going horizontally across the PTOP) that will make 26. The 11 is the number of EVENS Covered (EC) as the PPsets zig-zag diagonally down the PTOP. If we add double this EC - 1 to the EVEN 26, we get the EVEN Ending of 46 as: 2(11-1) + 26 = 46. So this Trail alone inclusively covers the EVENS 26-46, although their will be some holes. To fill the holes, we look at the Trails that started up above this 23 Trail.
For the Specific set of equations exclusively for the 3,P2 sets, where ∆ = P2 - 3 (see Table 45: Equations):
2EC = P2 -1
Ending EVEN Covered = Ee = 2(EC - 1) + EVEN
| 5 | 13 | 5 | 4 | 1 | 16: 2 | 6 | 26 | 16 |
|---|---|---|---|---|---|---|---|---|
| 6 | 17 | 6 | 2 | 4 | 20: 2 | 8 | 34 | 20 |
| 7 | 19 | 7 | 4 | 3 | 22: 3 | 9 | 38 | 22 |
We can readily see that the 17 and 19 Trails, when their EVENS are added to their 2EC-1, respectively, will equal or exceed the EVEN of the NEXT PRIME up by the GAP=6.
Take Trail 17: EVEN = 20 with EC = 8. 2(8-1) + 20 = 34.
Take Trail 19: EVEN = 22 with EC = 9. 2(9-1) + 22 = 38.
And these Trails 17 and 19 will overlap the Trail 23 EC span, filling in any and all holes between it and the next Trail 29.
| 9 | 29 | 9 | 2 | 7 | 32: 2 | 14 | 58 | 32 |
|---|---|---|---|---|---|---|---|---|
For completeness, we can see that Trail 13, while reaching Trail 23 at it’s start, does not overlap any further.
Take Trail 13: EVEN = 16 with EC = 6. 2(6-1) + 16 = 26. We also can see that 13 + 13 = 26.
~~~
The PPset Trails for EVEN 26 gives 3 PPsets via the overlapping Trails 17, 19 and 23, AND, their overlapping Trails extend past the next 3 EVENS (28, 30 and 32), ensuring that they are “covered” with PPsets in the Gap jump to the next PRIME (29). All very neat and clean.
The actual PPsets ∑s equal the EVEN 26:
which comes about more simply as the core Axis value ± steps away:
But what about a larger Gap? How about Trail 113, EVEN = 116 and a Gap of 14 to the next Trail 127? (See image from Table 36.)
Trail 113 is overlapped by Trails 73, 79, 97, 103, and 109 that account for the 6 PPsets that will form the EVEN = 116 (the 3,113 PPset is included in the tally and you can follow it in Table 43). Again, from Table 46:
| 1 | 3 | 1 | 2 | -1 | 6: 1 | 1 | 6 | 6 |
|---|---|---|---|---|---|---|---|---|
| 2 | 5 | 2 | 2 | 0 | 8: 1 | 2 | 10 | 8 |
| 3 | 7 | 3 | 4 | -1 | 10: 2 | 3 | 14 | 10 |
| 4 | 11 | 4 | 2 | 2 | 14: 2 | 5 | 22 | 14 |
| 5 | 13 | 5 | 4 | 1 | 16: 2 | 6 | 26 | 16 |
| 6 | 17 | 6 | 2 | 4 | 20: 2 | 8 | 34 | 20 |
| 7 | 19 | 7 | 4 | 3 | 22: 3 | 9 | 38 | 22 |
| 8 | 23 | 8 | 6 | 2 | 26: 3 | 11 | 46 | 26 |
| 9 | 29 | 9 | 2 | 7 | 32: 2 | 14 | 58 | 32 |
| 10 | 31 | 10 | 6 | 4 | 34: 4 | 15 | 62 | 34 |
| 11 | 37 | 11 | 4 | 7 | 40: 3 | 18 | 74 | 40 |
| 12 | 41 | 12 | 2 | 10 | 44: 3 | 20 | 82 | 44 |
| 13 | 43 | 13 | 4 | 9 | 46: 4 | 21 | 86 | 46 |
| 14 | 47 | 14 | 6 | 8 | 50: 4 | 23 | 94 | 50 |
| 15 | 53 | 15 | 6 | 9 | 56: 3 | 26 | 106 | 56 |
| 16 | 59 | 16 | 2 | 14 | 62: 3 | 29 | 118 | 62 |
| 17 | 61 | 17 | 6 | 11 | 64: 5 | 30 | 122 | 64 |
| 18 | 67 | 18 | 4 | 14 | 70: 5 | 33 | 134 | 70 |
| 19 | 71 | 19 | 2 | 17 | 74: 5 | 35 | 142 | 74 |
| 20 | 73 | 20 | 6 | 14 | 76: 5 | 36 | 146 | 76 |
| 21 | 79 | 21 | 4 | 17 | 82: 5 | 39 | 158 | 82 |
| 22 | 83 | 22 | 6 | 16 | 86: 5 | 41 | 166 | 86 |
| 23 | 89 | 23 | 8 | 15 | 92: 4 | 44 | 178 | 92 |
| 24 | 97 | 24 | 4 | 20 | 100: 6 | 48 | 194 | 100 |
| 25 | 101 | 25 | 2 | 23 | 104: 5 | 50 | 202 | 104 |
| 26 | 103 | 26 | 4 | 22 | 106: 6 | 51 | 206 | 106 |
| 27 | 107 | 27 | 2 | 25 | 110: 6 | 53 | 214 | 110 |
| 28 | 109 | 28 | 4 | 24 | 112: 7 | 54 | 218 | 112 |
| 29 | 113 | 29 | 14 | 15 | 116: 6 | 56 | 226 | 116 |
| 30 | 127 | 30 | 4 | 26 | 130: 7 | 63 | 254 | 130 |
What about the Gap = 14 going to the Trail 127, EVEN = 130? Overlapping Trails 71, 83, 89, 101,107 and 113 combine with the 127 to account for the 7 PPsets that will form EVEN = 130.
Of course to account for all the EVENS between Trail 113 and 127 — EVENS 116 to 130, we have Trails 59 to and including 127 in various combinations to account for that. We can easily see this on Table 46, lines 16-30, where each has an Ee (118–254) that meets or exceeds those EVENS (116–130). Altogether, there are some 80 PPsets that account for these 15 EVENS 116-130. Easily done.
What if you want to know specifically who covers, say EVEN 128? Looking at the full table, line 18, we see that Trail 67 and above have Ee > 128. How can we determine that the 19+109, 31+97 and 61+67 PPsets are the ones we are looking for?
Without even knowing the values for the Column 6 (Table 46): EVEN, ∑# of PPsets, one can:
look at an expanded PTOP
look at an expanded BIM
calculate using this trick:
on Table 46, find where EVEN 128 would be located between line 17 and 18 as 1/2 of 128 = 64
see that PRIMES 61 & 67 on either side = 128 when added together and both are PRIMES
knowing from the BIM that ALL PPsets are symmetrical about the center Axis core that points to the 90° R-angled isosceles triangle that each set forms, look for two PRIME Trails that are symmetrical to the 64 slot like the 61 & 67
the next pair out would be 31 & 97, followed by 19 & 109
this is easily calculated as the core Axis value ± steps away:
their ∑s equal the EVEN 128:
61 + 67 = 128
31 + 97 = 128
19 + 109 = 128.
We can confirm this on the PTOP (Table 35), and, of course, directly on the BIM. Tables 43 and 44 can also confirm ALL EVENS up to 2000. One can also use an online calculator to get the results.
it can be quite helpful to follow these examples directly on the BIM. The visualizations of how the symmetrical PPsets contributed from the separate, individual PRIME Trails line up their 90° R-angled isosceles triangles over the central core with each of their respective apexes inline and pointing towards the EVEN that they are forming. On the Axis, one can easily see the symmetrical steps from the core to each PPset.
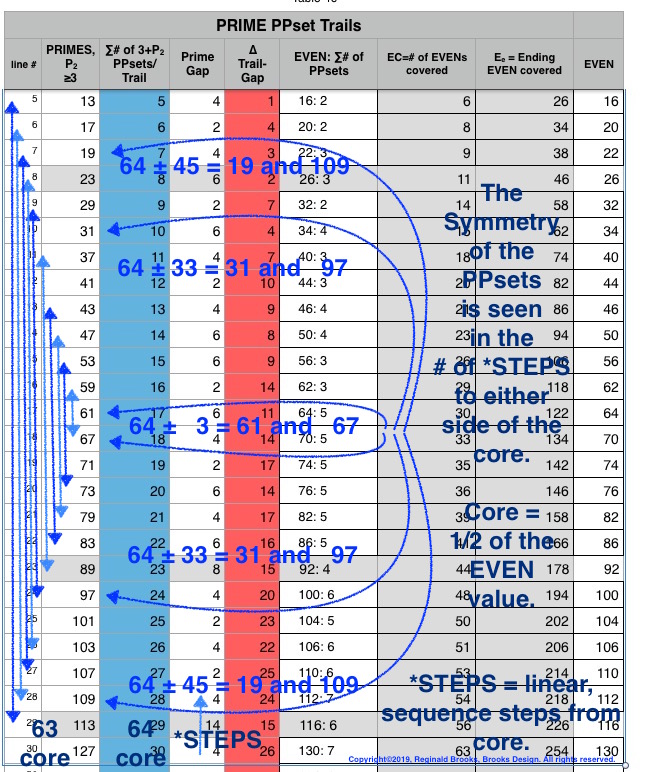
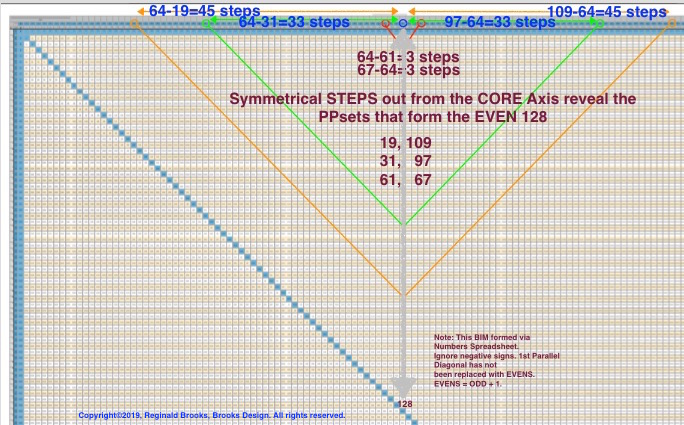
 (See the PDF versions for clear details.)
(See the PDF versions for clear details.)
What if you want to know specifically who covers, say EVEN 126? Looking at the full table, line 18, we see that Trail 67 and above have Ee > 126. How can we determine that the
13+113
17+109
19+107
23+103
29+97
37+89
43+83
47+79
53+73
59+67
PPsets are the ones we are looking for?
Without even knowing the values for the Column 6 (Table 46): EVEN, ∑# of PPsets, one can:
look at an expanded PTOP
look at an expanded BIM
calculate using this trick:
on Table 46, find where EVEN 128 would be located between line 17 and 18 as 1/2 of 126 = 63
see that PRIMES 59 & 67 on either side = 126 when added together and both are PRIMES
knowing from the BIM that ALL PPsets are symmetrical about the center Axis core that points to the 90° R-angled isosceles triangle that each set forms, look for two PRIME Trails that are symmetrical to the 63 slot like the 59 & 67
the next pair out would be 53 & 73, followed by 47 & 79.
this is easily calculated as the core Axis value ± steps away:
63 ± 4 = 59 and 67
63 ± 10 = 53 and 73
63 ± 16 = 47 and 79
63 ± 20 = 43 and 83
63 ± 26 = 37 and 89
63 ± 34 = 29 and 97
63 ± 40 = 23 and 103
63 ± 44 = 19 and 107
63 ± 46 = 17 and 109
63 ± 50 = 13 and 113
their ∑s equal the EVEN 126:
Towards the bottom of Table 46, lines 1092 - 1107, there is a good run of PRIME Gaps in close proximity. Below is the table in plain form with the same column headings:
| line # | PRIMES, P**2≥3** | ∑# of 3+P**2PPsets/Trail** | Prime Gap | ∆ **Trail-Gap** | EVEN: ∑# of**PPsets** | EC=# of EVENs covered | E**e = Ending EVEN covered** | EVEN |
|---|---|---|---|---|---|---|---|---|
| 1080 | 8681 | 1080 | 8 | 1072 | 94 | 4340 | 17362 | 8684 |
|---|---|---|---|---|---|---|---|---|
| 1081 | 8689 | 1081 | 4 | 1077 | 100 | 4344 | 17378 | 8692 |
| 1082 | 8693 | 1082 | 6 | 1076 | 89 | 4346 | 17386 | 8696 |
| 1083 | 8699 | 1083 | 8 | 1075 | 96 | 4349 | 17398 | 8702 |
| 1084 | 8707 | 1084 | 6 | 1078 | 132 | 4353 | 17414 | 8710 |
| 1085 | 8713 | 1085 | 6 | 1079 | 92 | 4356 | 17426 | 8716 |
| 1086 | 8719 | 1086 | 12 | 1074 | 112 | 4359 | 17438 | 8722 |
| 1087 | 8731 | 1087 | 6 | 1081 | 101 | 4365 | 17462 | 8734 |
| 1088 | 8737 | 1088 | 4 | 1084 | 136 | 4368 | 17474 | 8740 |
| 1089 | 8741 | 1089 | 6 | 1083 | 93 | 4370 | 17482 | 8744 |
| 1090 | 8747 | 1090 | 6 | 1084 | 138 | 4373 | 17494 | 8750 |
| 1091 | 8753 | 1091 | 8 | 1083 | 104 | 4376 | 17506 | 8756 |
| 1092 | 8761 | 1092 | 18 | 1074 | 111 | 4380 | 17522 | 8764 |
| 1093 | 8779 | 1093 | 4 | 1089 | 91 | 4389 | 17558 | 8782 |
| 1094 | 8783 | 1094 | 20 | 1074 | 95 | 4391 | 17566 | 8786 |
| 1095 | 8803 | 1095 | 4 | 1091 | 125 | 4401 | 17606 | 8806 |
| 1096 | 8807 | 1096 | 12 | 1084 | 124 | 4403 | 17614 | 8810 |
| 1097 | 8819 | 1097 | 2 | 1095 | 102 | 4409 | 17638 | 8822 |
| 1098 | 8821 | 1098 | 10 | 1088 | 90 | 4410 | 17642 | 8824 |
| 1099 | 8831 | 1099 | 6 | 1093 | 93 | 4415 | 17662 | 8834 |
| 1100 | 8837 | 1100 | 2 | 1098 | 141 | 4418 | 17674 | 8840 |
| 1101 | 8839 | 1101 | 10 | 1091 | 93 | 4419 | 17678 | 8842 |
| 1102 | 8849 | 1102 | 12 | 1090 | 91 | 4424 | 17698 | 8852 |
| 1103 | 8861 | 1103 | 2 | 1101 | 93 | 4430 | 17722 | 8864 |
| 1104 | 8863 | 1104 | 4 | 1100 | 118 | 4431 | 17726 | 8866 |
| 1105 | 8867 | 1105 | 20 | 1085 | 121 | 4433 | 17734 | 8870 |
| 1106 | 8887 | 1106 | 6 | 1100 | 148 | 4443 | 17774 | 8890 |
| 1107 | 8893 | 1107 | 30 | 1077 | 94 | 4446 | 17786 | 8896 |
| 1108 | 8923 | 1108 | 6 | 1102 | 95 | 4461 | 17846 | 8926 |
| 1109 | 8929 | 1109 | 4 | 1105 | 125 | 4464 | 17858 | 8932 |
| 1110 | 8933 | 1110 | 8 | 1102 | 95 | 4466 | 17866 | 8936 |
| 1111 | 8941 | 1111 | 10 | 1101 | 101 | 4470 | 17882 | 8944 |
| 1112 | 8951 | 1112 | 12 | 1100 | 104 | 4475 | 17902 | 8954 |
| 1113 | 8963 | 1113 | 6 | 1107 | 96 | 4481 | 17926 | 8966 |
| 1114 | 8969 | 1114 | 2 | 1112 | 84 | 4484 | 17938 | 8972 |
| 1115 | 8971 | 1115 | 28 | 1087 | 104 | 4485 | 17942 | 8974 |
| 1116 | 8999 | 1116 | 2 | 1114 | 110 | 4499 | 17998 | 9002 |
| 1117 | 9001 | 1117 | 6 | 1111 | 95 | 4500 | 18002 | 9004 |
| 1118 | 9007 | 1118 | 4 | 1114 | 133 | 4503 | 18014 | 9010 |
| 1119 | 9011 | 1119 | 2 | 1117 | 96 | 4505 | 18022 | 9014 |
| 1120 | 9013 | 1120 | 16 | 1104 | 119 | 4506 | 18026 | 9016 |
Without even knowing the values for the Column 6 (Table 46) which have been inserted here: EVEN, ∑# of PPsets, one can take EVEN 8872:
look at an expanded PTOP
look at an expanded BIM
calculate using this trick: (see *below for a simple Universal calculation method as shown in Table 45: Equations.)
on Table 46, find where EVEN 8872 would be located as the core Axis value between lines 601 and 602 as 1/2 of 8872 = 4436
see that PRIMES 4423 & 4441 on either side = 8864 when added together and both are PRIMES we are close
knowing from the BIM that ALL PPsets are symmetrical about the center core that points to the 90° R-angled isosceles triangle that each set forms, look for two PRIME Trails that are symmetrical to the 4436 slot like the 93 PPsets that equal EVEN 8872:
as before, these can be simplified as:
We can further simplify by applying these Universal (vs Specific, see Table 45:) equations:
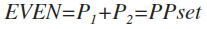
let S = steps, E = EVEN = 2(core Axis value) = 2(Ax), as E/2 = Ax
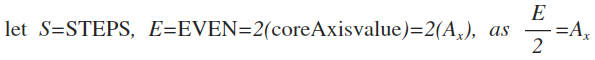
S = P2 - E/2 = P2 - Ax
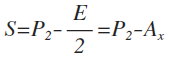
the PPset for a given EVEN:
P2 = S + E/2 = S + Ax
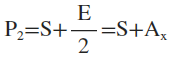
P1 = P2 - (2S)
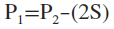
2S = P2 - P1
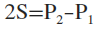
S = AX - P1
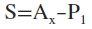
Example: 3,5 PPset for EVEN = 8: S = P2 - E/2 = P2 - Ax 1 = 5 -4
P2 = S + E/2 = S + Ax
5 = 1 + 4
P1 = P2 - (2S) 3 = 5 - (2*1)
And, as P1 = E - P2, or E = P1 + P2
P1 = P2 - (2S) = E - P2
2P2 - E = 2S 2(5) - 8 = 2(1) S = 1
As S = (2P2 - E)/2
S = (2P2 - E)/2 = P2 - E/2
2P2/2 - E/2 = P2 - E/2
P2 - E/2 = P2 - E/2 = S
P2 - Ax = P2 - Ax = S
The built-in symmetry of the PPsets around the core Axis value is easily calculated as these four examples show:
EVEN 24 with core Axis value (Ax) = 24 / 2 = 12 with 3 PPsets:
P1 = P2 - (2S)
as S = P2 - E/2 = P2 - Ax
11,13 13-12 = 1 13 - (2x1) = 11
7,17 17-12 = 5 17 - (2x5) = 7
5,19 19-12 = 7 19 - (2x7) = 5
EVEN 26 with core Axis value = 26 / 2 = 13 with 3 PPsets:
P1 = P2 - (2S)
as S = P2 - E/2 = P2 - Ax
13,13 13-13 = 0 13 - (2x0) = 13
7,19 19-13 = 6 19 - (2x6) = 7
3,23 23-13 = 10 23 - (2x10) = 3
EVEN 22 with core Axis value = 22/2 = 11 with 3 PPsets:
P1 = P2 - (2S)
as S = P2 - E/2 = P2 - Ax
11,11 11-11 = 0 11 - (2x0) = 11
5,17 17-11 = 6 17 - (2x6) = 5
3,19 19-11 = 8 19 - (2x8) = 3
EVEN 100 with core Axis value = 100 / 2 = 50 with 6 PPsets:
P1 = P2 - (2S)
as S = P2 - E/2 = P2 - Ax
47,53 53-50 = 3 53 - (2x3) = 47
43,57 57-50 = 7 57 - (2x7) = 43
41,59 59-50 = 9 59 - (2x9) = 41
29,71 71-50 = 21 71 - (2x21) = 29
17,83 83-50 = 33 83 - (2x33) = 17
11,89 89-50 = 39 89 - (2x39) = 11
~~~~~~~~ ⁃
As one moves successively along the EVENS, the Trails get longer and longer, adding one new member for each successive PS (See Tables 44-46.). This rate of increase far exceeds the size and incidence rate of the PRIME Gaps (See Tables 42 and 46.), ensuring that for every EVEN ≥6, there is at least one PPset of ODD PRIMES that will form it. Actually, as we have shown, there are always a minimum of 2 sets of PPsets that form the EVENS (≥14, including 10).
Table 44 shows how ∑s of the number of PPsets/ EVEN grows. It increases such that for every 60 successive EVENS on average, the ∑ increases by 3 (as calculated from 4-1080).
For example:
Columns generally have 60 entries ending in multiples of 120.
∑of PPsets per column Ave/Col
Col A 262 / 59 = 4.4 = 4
Col B 516 / 60 = 8.6 = 9
Col C 718 / 60 = 12 = 12
Col D 930 / 60 = 15.5 = 16
Col E 1076 / 60 = 17.9 = 18
Col F 1267 / 60 = 21.1 = 21
Col G 1302 / 60 = 21.7 = 22
Col H 1534 / 60 = 25.6 = 26
Col I 1687 / 60 = 28.1 = 28
PTOP: Periodic Table Of PRIMES & theGoldbach ConjectureINTRODUCTIONSTATEMENT: Layout & EssentialsThere are five sets of data to consider:FINDINGS & PROOFSUMMARY and CONCLUSIONDATA: Images and TablesDATA: Images and TablesREFERENCES
It is worth repeating here from above:
As seen in Table 44, EVEN 68 it the last EVEN to only have 2 PPsets, EVEN 128 is the last to have 3, 332 the last 6, 398 the last 7, 488 the last 9, 632 the last 10, 878 the last 14,…as the table shows the progression steadily goes forth never regressing by more than 1 or 2 to a previous lower value. The number of PPsets for:
If we take a sampling (from Table 46), the ∑# of PPsets and and divide by their respective EVENS, we get the percentage incidence of:
This built-in geometry provides the necessary coverage that ALL EVENS (≥14) will easily be covered by two or more PPsets. The geometry defines the algebra = algebraic geometry.
The Goldbach Conjecture is proven. With the EVENS having been actually tested for compliance with the conjecture up to 4x10**18, one can say that it is statistically impossible for any of the holes not to be covered by the PPset Trails no matter what size EVEN is considered! The largest confirmed PRIME Gap of 1550 would have —————
Finally — though, not really — one is left with the very strong impression that the PRIMES — of all things — actually demonstrated some very fractal-like behavioral patterns: let the essence of a fractal be r3 — redundant, reiterative and repeating — that leads to some form of self-similarity. On the PTOP we see the same PS — redundant, reiterative and repeating — informing each PPset Trail at each successive PS number down the left-side vertical column, forming the Trails zig-zagging diagonally. On the BIM — with its stealthily hidden PTOP — we see both the aggregate PPsets that inform the EVENS, and, the PPset Trails presenting 90° R-angled isosceles triangles — as redundant, reiterative and repeating — forms! Looks like a fractal, walks like a fractal, quacks like a fractal,…! Does it make a self-similar gestalt?
PTOP: Periodic Table Of PRIMES & theGoldbach ConjectureINTRODUCTIONSTATEMENT: Layout & EssentialsThere are five sets of data to consider:FINDINGS & PROOFSUMMARY and CONCLUSIONDATA: Images and TablesDATA: Images and TablesREFERENCES
Here is the index of the five sets of data to consider (click links to go):
BIM (BBS-ISL Matrix): grid visualizations that overview the entire work
PTOP: the actual Table
PTOP: Analysis
Reference
PRIME PPset Trails
BIM (BBS-ISL Matrix): grid visualizations that overview the entire work












PTOP: the actual Table




PTOP: Analysis





Reference





PRIME PPset Trails




PTOP: Periodic Table Of PRIMES & theGoldbach ConjectureINTRODUCTIONSTATEMENT: Layout & EssentialsThere are five sets of data to consider:FINDINGS & PROOFSUMMARY and CONCLUSIONDATA: Images and TablesDATA: Images and TablesREFERENCES
Unexpected Beauty in Primes - Cantor’s Paradise - Medium
https://medium.com/cantors-paradise/unexpected-beauty-in-primes-b347fe0511b2
File:Goldbach conjecture with Excel.pdf - Wikimedia Commons
https://commons.wikimedia.org/wiki/File:Goldbach_conjecture_with_Excel.pdf
Goldbach's conjecture | letsprovegoldbach Blog
http://letsprovegoldbach.altervista.org/la-congettura-di-goldbach/
5 - The Goldbach's conjecture with Excel - By reading Archimedes
https://sites.google.com/site/byreadingarchimedes/the-goldbach-s-conjecture-with-excel
Google Translate of the original Italian webpage above
A table of prime counts pi(x) to 1e16
http://www.trnicely.net/pi/pix_0000.htm Prime Number Theorem
numbers.computation.free.fr/Constants/Primes/pixtable.html
http://numbers.computation.free.fr/Constants/Primes/pixtable.html
PTOP: Periodic Table Of PRIMES & theGoldbach ConjectureINTRODUCTIONSTATEMENT: Layout & EssentialsThere are five sets of data to consider:FINDINGS & PROOFSUMMARY and CONCLUSIONDATA: Images and TablesDATA: Images and TablesREFERENCES
MathspeedST: TPISC Media Center
Artist Link in iTunes Apple Books Store: Reginald Brooks

Back to Part I of the BIM-Goldbach_Conjecture.
Back to Part II of the BIM-Goldbach_Conjecture.
Back to Part III of the BIM-Goldbach_Conjecture.
Reginald Brooks
Brooks Design
Portland, OR
brooksdesign-ps.net
~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~ ~~