~art theory 101~ The Geometry of Music, Art and Structure ...linking science, art and esthetics

THE GEOMETRY OF MUSIC, ART AND STRUCTURE ... LINKING SCIENCE, ART AND ESTHETICS

Copyright© 2009, Reginald Brooks. All rights reserved

ABSTRACT

That simple geometric principles can be responsible for the manifestation of the multitudes of beauty, diversity and richness of Nature is further supported here in this paper. The Inverse-Square-Law (ISL), a simple geometric principle, is shown to be the common link between physics, chemistry, biology, and the science and esthetics of music and art. Nature has incorporated the ISL as the major game rule to building the cosmos. Our perception of pleasing form, color and sound is prophetically built into our sensory being, our biologic evolution, and our structural past. Key to our understanding of the geometry of the ISL is the interference of complementary waveforms.

Nature's game rule has separate game plans for color and music. In color, complements form neutrals, while in music complements form harmonic resonates. Our limited perception of light (color) to only one octave belies the notion introduced here that every photon of the electromagnetic spectrum has a complementary photon above and below its given wavelength as surely and as explicitly defined as every musical note has a complementary note a perfect fifth above and below. Both complementary patterns of color (light) and music (sound) are defined by the same game rule, the ISL. The harnessing and use of light energy may be enhanced and controlled by focusing on this new complement relationship. Key words: geometry, music, light, art, structure, Inverse-Square-Law, complements, color, key.

1. INTRODUCTION

There is an innate response to design harmony, unity and simplicity...commensurate forms appeal to our sense of order and beauty (symmetry). Diversity, especially when brought about by multiples and changes of scale of the originally simple and harmonious, endears our esthetic as well as intellectual response (asymmetry).

In our art and in our science, resonance...be it visual, aural, physical or mental...provides the keystone to viable, stable structures and our responses to them. The wave-particle duality of existence ensures that we are present as both a part of the unity (wave) and as an individual (particle) simultaneously, despite the feeling we get that we are one or the other.

One of the simplest visual examples (in many forms) with deep resonating significance is the variously wonderful interference patterns (wave crests troughs and nodes) generated by a series of two or more disturbances upon the form of water. Here many of Nature's design variables find expression in the changed form of the water...be it the waves on the beach, the lace of a waterfall, or the ripples in a stream. Variables such as:

symmetry vs. asymmetry

simplicity vs. diversity

harmonic vs. disharmonic

order vs. disorder(chaos)

static vs. kinetic

wave vs. particle

analog vs. digital

space vs. time.

Mendeleev's Periodic Table of the Elements linked chemistry to physics; Watson and Crick's double helix linked biology to chemistry; while Freud and Jung linked psychology to biology. Darwin linked biologic evolution to local space-time variations (the environment). Einstein, of course, linked all matter and energy to spacetime itself.

These and other advancements in our understanding of Nature have stood on the shoulders of ancient Greek thought which maintained a profound belief in an ideal geometry forming the basis for...and consequently the interconnectedness of...all that we are, know, and can be.

There is an innate response to design harmony, unity and simplicity ...commensurate forms appeal to our sense of order and beauty (symmetry). Diversity, especially when brought about by multiples and changes of scale of the originally simple and harmonious, endears our esthetic as well as intellectual response (asymmetry).

In our art and in our science, resonance...be it visual, aural, physical or mental...provides the keystone to viable, stable structures and our responses to them.

The wave-particle duality of existence ensures that we are present as both a part of the unity (wave) and as an individual (particle) simultaneously, despite the feeling we get that we are one or the other.

Our esthetic response, though highly tempered by the prevailing attitudes (psychology) of the times, is generally not so much as free will as of free choice. However, our increased awareness of choice may result in even better means of communication, expression and understanding. While colors may allow one to see specific sounds, and vice versa, both color and sound patterns can communicate definite shapes and forms of physical, and especially virtual, realty.

Nature typically includes other important options including the notions and consequences of random versus non-random interactions. Here concepts like selection, mutation and/or hybridization, and transformation ensures a fabulously rich and unbounded sense of possibilities. It is typically the non-random interactions that form the basis for our laws of physics that describe Nature's design.

In the West, Newtonian physics was wanton to describe clock tight space, time, velocity and size as 3D, absolute, slow and large, respectively. It was rational and predictable.

It was also the time for beautiful art, music and architecture. Rameau advanced music theory to form the diatonic scales...major and minor keys and the Circle of Fifths...culminating in the concept of tonality. Helmholtz, working from Newton's discoveries, advanced color theory to include the physiological role of perception in the experience of color sensation.

Of course, the Newtonian era grew out of the Renaissance, itself a rebirth and remake of the best of Greek thought...including the belief in simpler, but in many ways more profound, design parameters as suggested by simple geometric shapes and sizes as well as the simple, but profound relationships between dimensions as expressed in the Divine (Golden) Proportions... creating standards of beauty perhaps never surpassed.

Re-examination of those simple fundamental relationships in Nature's design leads to the Einsteinian revolution of variable spaces and times, in which large velocities could actually effect the size and mass of things.

Along with the development of quantum physics...in which anything that is possible can happen, only the possibilities of it actually occurring in a given lifetime are strictly probabilistically determined...we are now extended into the post-Einsteinian cosmology era. Multiple dimensions of space and time pulsing in and out of existence actually form the matter and energy. Constructive interference at every level of existence up to and including the cosmos itself provides that resonance, that pattern of viability. Because the cosmos knows no rest, all such resonant patterns are in flux, either forming or decaying...thus perhaps our current attraction to the dynamics and design of asymmetry. Is it a rational mind in an irrational universe or an irrational mind in a rational universe?

The dynamical nature of the cosmos is defined by a mathematical relationship known as the Inverse-Square-Law (ISL) ... dynamical influence (s) is inversely proportional to the distance of separation squared. That the force of gravity and the force of electromagnetism follow the ISL is well established. It will be the purpose of this paper to demonstrate that the ISL also defines:

I. The basis for theory and practice in Western occidental music for the division of the monochord and the geometry of simple ratio numbers, forming the major and minor diatonic scales, leading to the concept of tonality and key relationships as exemplified in the Circle of Fifths and the Golden Rectangle (GR);

II. The basis for theory and practice in art for color theory, the additive color spectrum (chromicity diagrams) and color complements; and,

III. The structural basis of the atom, and subsequently through the geometry of the GR the structural basis of the double helix of DNA revealing the interrelationships of sound, sight and structure in art and Nature.

The division of the monochord can be traced back at least to the 27th century B.C., where Ling Lun of China created a five tone pentatonic scale with the intervals of 1/1, 3/2, 9/8, 27/16, 81/64. Pythagoras of Samos delineated a harmonic proportioning of the monochord into simple divisions of 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, 1/8, etc., leading to Pythagorean turning based on perfect fifths.

A variety of tunings have evolved as the monochord is variously divided based on appropriate intervals pleasant to the ear (just temperament) to those given mathematical exactitude (equal temperament where the interval is derived from ¹²√2).

A common denominator is that all such diatonic tunings approximate the division of the monochord in such a fashion that is equivalent in geometric terms to one of nature's most fundamental laws-the inverse square law. The strength of the forces of gravity and electromagnetism both fall off inverse squarely of the distance of separation.

Geometrically, this may be viewed as the distance is doubled, the area of influence (force field concentration) is reduced by 1/4, as the distance is tripled the area is reduced by 1/9, when quadrupled the reduction is 1/16, and so on. The odd numbers when added in sequence equal the area, i.e. 1+3=4-^1/4, 1+3+5=9-^1/9, 1+3+5+7=16-^1/16, and so on.

Now, when simple harmonic divisions of the monochord are compared,

it is found that it is only the same odd numbers of divisions that define the musical intervals. Thus:

1 division is unison, 2 divisions equal the octave

3 is the fifth (3/2), 4 is the next octave

5 is the third (5/4), 6 is the fifth repeated (6/4=3/2),

7 is the seventh (7/4), 8 is the next octave

9 is the second (9/8), 10 is the third repeated (10/8=5/4),

11 is the fourth (11/8=33/24 or 4/3=32/24),

12 is the fifth repeated

13 is the sixth (13/8=39/24 or 5/3=40/24),

14 is the mseventh repeated

15 is the Mseventh (15/8).

These divisions, when geometrically defined, are shown as a color circle later in this work.

Fig. 1 Divisions of the monochords (M). The Pythagorean division of the M...which led to Just Intonation Tuning...was based on simple number ratios...simple divisions of the M...1/2---2/1, 1/3---3/2, 1/4---4/3, 1/5---5/4 and 5/3 and so on. Disregarding the length of the monochords, sequential monochords are divided by 1, 2, 3,...13 (right axis) revealing the musical pitches thus generated when the ratios of those frequencies are compared (left axis). For example, dividing M by 4 gives the ratios of 4/1, 4/2, 4/3 and 4/4. Only 4/3 is different, the other three are just octaves. 4/3=1.334=F. Next up is 5. 5/1 and 5/5=octaves. 5/2=2.5 (divide that by 2=1.25=E). 5/3=1.667= A and 5/4=1.25=E. And so on.

1. EXPOSITION

Nature's design for the cosmos can in part be distilled into fundamental laws of physics which appear to be the simplest and most immutable blueprints for the size, frequency, velocity, mass and energy of being. The ISL, being one of those fundamental laws of physics, relates the degree or concentration of an influence (or force) to various distances of separation. Thus it is written:

Concentration 1

of = _______

influence d²

(d=distance)

as the distanced is doubled, the influence diminishes by 1/4. This is easily visualized by looking at the spray of influence which is itself easily analyzed as shown in Fig. 1.

25 squares = 1+ 3 + 5 + 7 + 9

16 squares = 1+ 3 + 5 + 7

9 squares = 1+ 3 + 5

4 squares = 1+ 3

1 square = 1

Fig. 2 Geometry of the ISL.

Notice that a simple pattern, called the odd number summation series, develops to describe this simple geometric law. The odd numbers 1 . . .3. . .5. . .7. . .and so on, which added to each other form the sums 1 . . . 4 . . . 9 . . . 1 6. . .and so on, the square roots of which form the series 1 . . .2. . .3. . .4. . .and so on.

There are other ways to visually demonstrate the ISL and we will be using some of them to validate our premises. But keep in mind that they all relate back to the simple principles presented here.

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

2.1 Premise 1...Music and the ISL

The divisions of the monochord and the relationship of these simple number ratios to musical intervals (the Pythagorean division of the monochord) and their subsequent placement by the musical ear into major and minor triads forming the major and minor diatonic scales...ultimately identifying a fundamental key and thus a basis for tonality in Western music as first presented by Rameau...is a direct manifestation of the ISL.

The monochord (M) is an ideal string (wire) that accurately relates Nature's relationship between space and time, here as frequency of vibration and length of wavelength. Multiplied together, they always give a constant value, thus as frequency (ν) increases, the wavelength (λ) decreases and vice versa.

If one exactly doubles (or halves) the frequency one gets the same key, only at a higher (or lower) pitch. Thus dividing the M in half (octave) and relating the pitch of one of these segments to the pitch of the full undivided monochord (unison), we get a simple ratio of 2/1=2, but no actual change in key. Successive octaves being at 3/1, 4/1,...

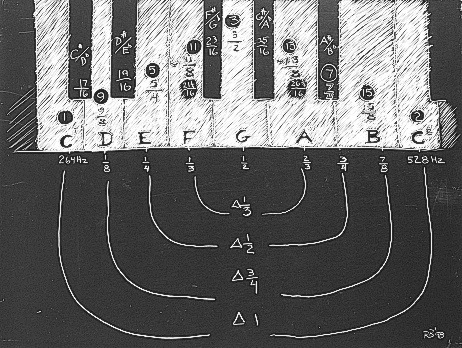
Fig 3. Division of the monochord as it appears on the piano keyboard. The encircled numbers on the piano keys show the simple number divisions of the M following the odd-numbered series of the Inverse Square Law. Below, the interval spans are depicted as the change...or difference of...one pitch ratio type to its related numerical type. Very symmetrical.

Now we are going to systematically relate the various simple divisions of the monochord geometrically on a circle, comparing this with the historical tuning systems of just intonation (JI...based on the relationship between simple divisions of the M resulting in sounds pleasing to the ear), and, to equal temperament (ET...the modern, compromised tuning scheme based on 12 equal intervals within the octave as defined by ¹²√2= 1.05946).

Since A=440 cycles per second (c/s) is the standard tuning ν, we will use this ν to compare each of the three tuning systems compared in this paper.

Using the scale for the key of C and working down from A=440 c/s, we have C at 262 c/s for equal temperament (ET), 264 c/s for just intonation (JI) and 264 c/s for our new geometric (G) tuning we are introducing here.

Fig 4. Pie Chart of the ISL ratios. The upper half is based on 16^ths. The lower half is based on 12^ths to accommodate the 1/3 and 2/3 ratios of F and A, respectively.

Geometrically on the circle diagrams, we will always start at the top 12 o'clock position as unison. Unison equals one=l/l=2/2=4/4=8/8=16/16, and naturally an octave above (or below) brings one full circle around to the same geometric position of the circle, as 2/1=4/2=8/4 and so on. It is the ratio of the subsequent ν's (corresponding to their lengths) that will place the resulting pitch at its location clockwise around the circle.

C¹ , C², C³; ...are the unison and octaves. Sharps are designated ^# , flats as ^b.

Thirteen divisions and a running chart will provide a visual and tabular account in the formation of the 12 semitones of the octave as presented in Table I and Fig. 7.To notice is that the very same sequence of odd numbers which forms the basis of the ISL (1, 3, 5, 7, 9, 11, 13, 15, 17,...) also informs the major divisions of the M...which ultimately defines the Western diatonic scales. A firm basis is thus established between the G, JI and ET tunings.

Fig. 5 Reference Pie Chart. It is all based on dividing the full circle into 16^ths. Notice that the Tonic (T) is always located at 0°, the Subdominant Complement (SDC), based on thirds, is at 120° and the Dominant Complement (DC), based on halves, is at 180°. This is valid for all keys, major and minor.

We also see a link between so called subjectively pleasing sounds to the ear and Nature's universal laws of both gravitational and EM interaction. What a coincidence. Harmony of the spheres and harmony to the ears defined by the same ISL.

The concept of tonality follows from the work of Rameau who in 1722 demonstrated that the ear will naturally separate out a series of tones, recognizing a fundamental bass tone and a series of chords (based on triads of thirds) related to this fundamental tone. When this series of chords are further related by being organized a Perfect Fifth above and below the fundamental chord, we have the basis for diatonic scales. When the triads in the chords are all major triads (M3 + m3), we have the major diatonic scale. When they are all minor triads (m3 + M3), we have the natural minor scale, and when two of the triads are minor (tonic and subdominant) and one is major (dominant), we have the basis for the harmonic minor scale. This musical thought analysis was based on the simple ratio number divisions of the M of JI. Tonality is perceived, identified and maintained by the listener of musical sounds that are related to each other harmonically by these simple ratios. The ratios for the major triad are built around 4:5:6 as:

E E^b G

5/4=1.25=M3^rd 6/5=1.20=m3^rd 6/4=3/2=1.5=P5^th

and from these those below can be derived:

D F A

9/8=1.125=M2^nd 4/3=1.34=P4^th 5/3=1.67=M6^th

B

15/8=1.875=M7^th

The ratios for the minor triads are built on 10:12:15 giving:

E^b E

12/10=6/5=1. 20=m3^rd 15/12=5/4=1.25=M3^rd

G D F

15/10=3/2=1. 5=P5^th 9/8=1.125=M2^nd    4/3=1 .34=P4^th

A B^b

8/5=1. 6=m6^th 9/5=1. 8=m7^th

These simple ideal ratios of just intonation form:

Major Triads Minor Triads

G-B -D dominant G-B^b-D

C-E-G tonic C-Eb-G

F-A-C subdominant           F-Ab-C

G, ET, and JI (with the diesis of 25/24 inserted to account for the 13 notes of the octave) are similar:

It is important to remember that we hear sound pitches over many octaves. Musical analysis of the tonal relationships within a key and when modulated by chord progression to a new key relate back to the single, reference octave ultimately. A progression of C Major octaves, like a long monochord, reveals the C Major diatonic/chromatic scale when wrapped around a circle, C¹ to C² as discussed. Yet, to show the dominant and sub-dominant complements of G and F, respectively, in their full tonic form, we must wrap the monochord now with them in the tonic position up on top, and in doing so, utilizing different parts of the octave above and below the reference octave. The same applies to color analysis.

C D E F G A B C¹ D E F G A B C² D E F G A B C³..

C D E F G A B G A B C¹ D E F D E F G A B C

F C G

E G B D   F^# A

A E            B

  D B^b A F E             C

C G D

Fig.6 The Division of the Monochord and the ISL (another view). Here is another graphic way to visualize how the ratios of the simple-number divisions of the monochord generate the 12 tone key pitches of the diatonic music scale. It is completely defined by the odd-number series...1, 3, 5, 7,...of the Inverse Square Law (ISL). See Figs 1-5.

Click HERE to enlarge image.

Table I. in graphic form. Click HERE to enlarge image.

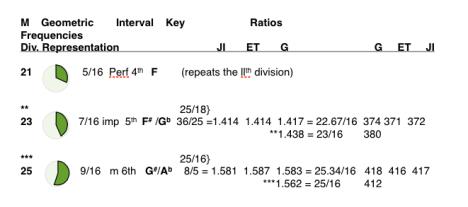
Table I.

Fig 7.

Table I and Fig. 7. Chart relating the ISL derived divisions of the monochord (M), geometric representation, interval, key designation, ratios and frequencies in the just intonation (JI), equal temperament (ET) and geometric (G) tunings. Note that geometrically, the complement of the fundamental key (here as C) is always 180° opposite on the circle (here as G). This complement, typically referred to as the dominant (or Perfect 5^th ) is always related to the fundamental key by the ratio 3/2 (1.50 x 264 = 396) and is located above the unison (tonic). Another complement, the subdominant (F), located a Perfect 5^th below unison (264 ÷ 1.5 x 2 = 352), becomes geometrically apparent when rotated to the unison position upon which the key of C will now be located 180° opposite and, therefore the new dominant of the key of F. A progression of Perfect 5t^hs will reveal all 12 notes of the octave, each note being seven steps above or below its Perfect 5^th complement. Every note when rotated to the key (unison) position, reveals its upper dominant complement at 180° opposite and its subdominant complement at 120°.

NEW: Piano Waves Interactive 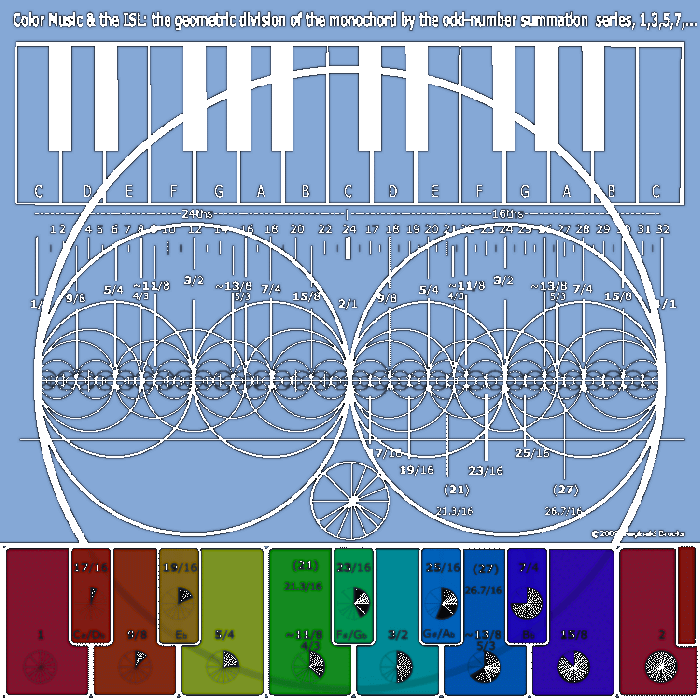Color_Music_The ISL Monochord

Fig. 7b. Music Color and the ISL (Inverse Square Law) interactive graphic.
NOTE: This link will take you to a new page within my new media net.art project the "Geometry of Music Color ... the role of the ISL" where much of the graphics from this white paper are recast into an interactive experience for the viewer. Various Color_Music_Composer pages are also featured.

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

2.2 Premise 2....Color and the ISL

The ISL informs the very foundation upon which modern color theory and practice rests.

The physics of color theory have evolved around the recognition that color is represented by a light wave/particle (photon) of a particular narrow frequency and wavelength, and that all hue identities can be accounted for by additive or subtractive mixtures of such colored photons present in the net light given off by the mixture/lens in question. These mixing operations have lead to the notions of primary, secondary and tertiary colors, and especially to that of complementarity as one places the color spectrum around the circle of the color wheel or chromicity diagram.

The physiology of color perception, including the remarkable phenomena of color constancy (Land, 1959) under various fields of perception, is linked to the ability of the rods and cones in our retinas to survey the spectrum of photon energies presented in a given view, to classify and assign the relative high, medium and low energies to their respective cone sensors. Our brains interpret these relative energy firings as the sensation of a color or group of colors. Unlike music, we "see" only one octave of color from red to violet (our brains see purple as the mixture of the two as there are no purple photons). There are, of course, a whole multitude of octaves of photon frequencies that comprise the EM spectrum, and perhaps if our retinas were sensitive to a larger visual range we would be able to see repetitions of red through violet at each octave above and below our present visual field. Nature appears to have a different game plan for our visual cortex than she does for our auditory cortex.

Our premise here is that the underlying game rules are the same and are mediated through the ISL. The game rules are the physics of sound and color. The game plan is how we, as sentient beings, have evolved to interact with our environment to selectively harness and process a portion of the available energy fields to which we are subjected.

In music, we have seen how from the multitude of sequential octaves of sound we can perceive some range...and within these octaves we can organize and perceive natural divisions (notes and intervals)...which can be arranged into groups (chords), which can be further arranged into unifying forms of scales in which rather precise relationships of harmony present themselves, giving rise to the concept of tonality. A key (no pun intended) relationship between the fundamental key of a scale and that key which is 3/2 of that fundamental key (ie. 50% of the way between the two octaves), is that of the Perfect 5^th. The 5^th above and below the octave is the complement to the fundamental key. The 5^th defines the dominant and subdominant key relationships to the tonic key.

The diatonic musical scale is to music what the color wheel/chromicity diagram is to color. Both being ultimately derived from the ISL...both following the same game rules.

In color, the game plan is a little different. Amongst the enormous multitude of EM frequencies/ wavelengths, our color game plan only allows us to perceive a small spectrum of these wavelengths, just shy of a full octave...between 750-400 nm (nanometers; note older standards use 700-400 nm).

Nevertheless, the color game rules operate the same in principle, as do the sound game rules. If one treats the visual octave of the EM spectrum as a M placed around a circle, one finds that the very same divisions of the M (circumference) seen in sound are applicable here in sight. The very same odd numbered divisions of the M seen in music can now be shown to form the primary and secondary colors of the color spectrum.

Of special importance here, as in music, is the concept of the complement. For every photon in the EM spectrum (visible or not) there is a dominant and subdominant or complementary color. The dominant complement is 3/2 above; the subdominant complement is 3/2 below, the tonic (fundamental) photon, using additive color mixing. See Figs.8-11.

Because the color game plan only allows us to see one octave of the EM spectrum, we can not see both the dominant and subdominant complements (Perfect 5^ths) except for the green/blue-green colors situated in the center of the visible spectrum. Most visible colors have either the dominant or sub-dominant complement visible, not both. But both surely exist because the physics of the color game rules, as in music, describe a physical interference pattern between a given frequency or wavelength and one that is 3/2 larger or smaller. This holds for every wavelength or frequency, be it of sound or light. The complement wavelength (frequency) leads to the first harmonic (constructive interference) with the tonic. In sound, this first harmonic amplifies the sound, while in sight it leads to a neutral...a loss of color.

Fig. 8. ISL-derived color wheel. The divisions of the red M are shown as ratios. Every color has a dual complement, one 3/2 above and one 3/2 below the tonic wavelength. This is the simplified color wheel with the 8 key colors plus their intermediates. The corresponding C Major diatonic scale, the SDC (subdominant complement), DC (dominant complement), and L (Locator) wavelengths for each color are shown, with two examples shown above for clarification. The T (tonic) is always found below the heavy white band, the DC under the white band, the SDC under the dashed band, and the Locator under the dotted band. The Locator wavelength points to the location outside of our normal visual octave, to an octave above or below, that that DC or SDC would be found, were our eyes sensitive to these wavelengths. Additive color. Click HERE to enlarge image.

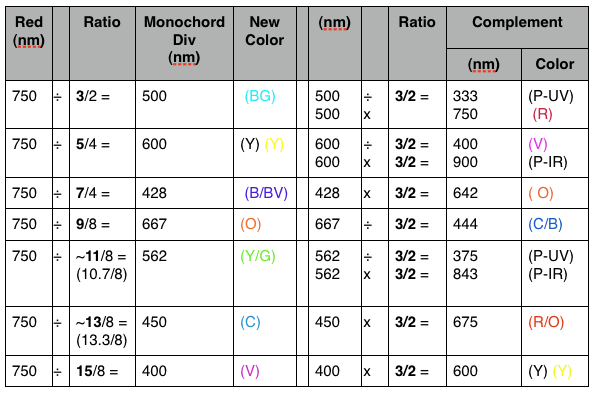
Table II. Notice that in this example using the far-red wavelength of 750 nm that the 1,3,5,7,9,11,13 and 15 divisions of the red monochord provide the common colors of the color wheel. The complementary color (3/2 above and below) in the right columns results when that color is now treated as the fundamental tonic color (as red was), whose monochord is now wrapped around the circle via the ISL divisions.

Red was chosen here because it begins the visible portion of the color octave, but any color can be subject to this plan.

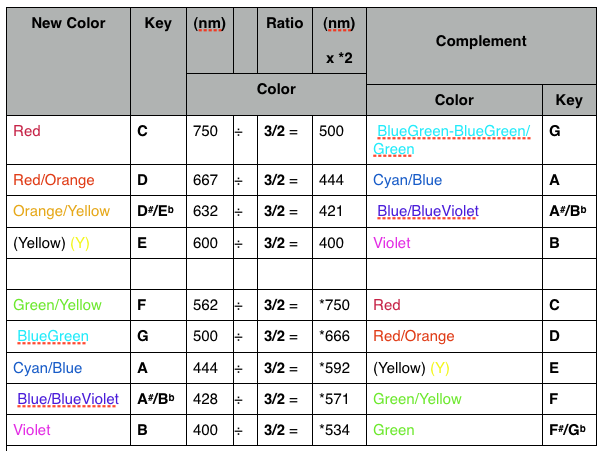
Table III. This table will help clarify by example...in simple terms...how each color wavelength of light when placed in its tonic position, will give up its dominant complement by division by 3/2...and, when necessary to return to the visible spectrum...multiplication by *2. It should be pointed out that this “complement” ...except for Red-BlueGreen...is NOT that which is directly OPPOSITE on the ISL Musical-Color Wheel. It is to be found...as in music...to be geometrically 3/2 from the frequency/wavelength of that key color in its tonic position. That translates to 7 semitones in the musical diatonic scale and 8 color steps on the wheel. Notice that…due to the inherent asymmetry and progression of the scale…that the forward and reverse complements of any tonic are not the same.

Every wavelength of light, visible or not throughout the EM spectrum, has this same complementary relationship to its two partner wavelengths, one 3/2 times the wavelength above and one divided by 3/2 below the wavelength in question (similar to the Perfect 5^th above and below the tonic key in music). We are using color designations in the optical or additive mixture scheme in this paper. See Table II.

The similarities in Nature's games rules for sound and light can perhaps best be seen in Figs. 9 and 10 where a progressive, double-sided monochord with the chromatic musical scale on top and its corresponding color scale below is laid out. In both, the correspondence of the ISL matched ratios is maintained. Note the dependence of each dominant and subdominant complement to the tonic location to which it is related. Complementary colors in the tonic red monochord, while true to our real life visual experiences, may very well have different "color" combinations in those octaves outside our normal visual range, in every way similar to the movement of Perfect 5^ths transposed serially through successive octaves. See Fig. 8.

*---------------------------7 steps-upper (music)------>*-------------------------------------------

C¹ C^# /D^b D D^#/E^b E F F^#/G^b G G^#/A^b A A^#/B^b B C²

R R/O O O/Y Y Y/G G G/BG BG BG/C C B BV V(P) R

^--------------------------8 steps-lower (color)--------->^--------------------------------------------

---------------------*------------- 7 steps-upper (music)-----------------*--------------------------

C² C^# /D^b D D^#/E^b E F F^#/G^b G G^#/A^b A A^#/B^b B C³

R R/O O O/Y Y Y/G G G/BG BG BG/C C B BV V(P) R

------------------(TK)---------------8 steps-lower (color)-*---------->(DC)-------------------------

--------------------------------------*---------------------------------------------------------------*-------

C³ C^# /D^b D D^#/E^b E F F^#/G^b G G^#/A^b A A^#/B^b B C⁴

R R/O O O/Y Y Y/G G G/BG BG BG/C C B BV V(P) R

--------------------------------------^--------------------------------------------------------------^--------

-------------------------------------------------------*-------------------------------------------------------

C⁴ C^# /D^b D D^#/E^b E F F^#/G^b G G^#/A^b A A^#/B^b B C⁵

R R/O O O/Y Y Y/G G G/BG BG BG/C C B BV V(P) R

--------------------------------------------------------^------------------------------------------------------

-----------*--------------------------------------------------------------*------------------------------------

C⁵ C^# /D^b D D^#/E^b E F F^#/G^b G G^#/A^b A A^#/B^b B C⁶

R R/O O O/Y Y Y/G G G/BG BG BG/C C B BV V(P) R

-----------^--------------------------------------------------------------^------------------------------------

------------------------------*-------------------------------------------------------------*------------------

C⁶ C^# /D^b D D^#/E^b E F F^#/G^b G G^#/A^b A A^#/B^b B C⁷

R R/O O O/Y Y Y/G G G/BG BG BG/C C B BV V(P) R

------------------------------^---------------------------------------------------------(SDC)<-------------

--------------------------------------------(TK)------------------------------------------------------------*

C⁷ C^# /D^b D D^#/E^b E F F^#/G^b G G^#/A^b A A^#/B^b B C⁸

R R/O O O/Y Y Y/G G G/BG BG BG/C C B BV V(P) R

-------------------------------------------(TK)--------------------------------------------------------->(DC)

Fig. 9. Double Monochord. Twelve upward transpositions of Perfect 5^th (Dominant Complements, DC) one for each chromatic key (7 octaves), are shown on the upper scale. Every note when treated as a Tonic Key (TK) has a DC 7 notes upward and a Sub-Dominant Complement (SDC) 7 notes below. Likewise, assigning ISL matched colors to each musical note (lower scale), reveals that each color note, when treated as a TK, has both a DC and a SDC color (8 color steps above or below), in octaves outside our normal visual range... complements whose "colors" may be different from those of the tonic red monochord that we know as our reference.

Fig 10. Music-Color Double Monochord. Musically, the 12 transpositions of Perfect 5^ths (DC), starting with C Major, are depicted on the outside. Note that every 7^th semitone locates the DC ahead of the T, or the SDC behind. On the inside track is the corresponding color monochord. Click HERE to enlarge image.

It is suggested here, that the dual complementary nature of each photon wavelength, conspicuous in their "absence" in our understanding of the normal visual octave, may explain color constancy under differing energy fields as discovered by Land. The presence of complements and other primaries from different EM octaves may invoke the perception of local color in the absence of its known visual wavelength or suitable additive mixture.

Fig. 11a. The ISL derived music-color wheel. The musical chromatic scale (C Major) is matched to the ISL ratios of the color wheel based on the visible color octave (far red λ of 750 nm as the tonic key). Steps for purple/violet-UV and purple/ red-IR close the circle. Simple ratios are shown way outside...their ratios based on 16^ths just inside...of the diatonic scale keys in the B&W inner circle. The color wavelengths are shown next...outside the color “key” designations (outer B&W). Below the music keys are their sound frequencies. Finally, the inner white disc in the B&W is encircled by the corresponding complement wavelengths of the respective color straight out from it. Click HERE to enlarge image.

Here below is an example of how to use Fig. 8, along with Figs 9-11 and Figs 13-17, and Table II above, to generate the true dominant color complements as one moves sequentially clockwise around the Circle of 5^ths beginning with Red-C Major. The reader may want to come back to this example after reading through the paper.

The Locator (L) in Fig. 8 ...shown as the color wavelength (dotted line) above or below the visible electromagnetic spectrum that we can actually perceive... is employed to “locate” the complement in the color “octave” outside our human view and to seamlessly connect the two open polar opposite ends of the visible spectrum into a circular repeating pattern...just as in music. Again, as in music, one has to place the color key in question in its appropriate Tonic (T) position at the top or equivalently count the appropriate number of half-steps (semi-tones) forward to reach the Dominant Complement (DC) or backward for the SubDominant Complement (SDC). For music this is 7 steps either way. For color it is 8. As a reminder...referring to the figures and Table II, the DC can be found mathematically by noting that it is always related to the T by the simple ratio of 3/2=1.5 or its inverse 2/3=0.667. In the example we will use both interchangeably depending on the needs. The reader may also notice that the Locator is always either one-half or double the Tonic (raising or lowering the “octave.”) All wavelengths are in nanometers.

Red-C Major 750 x 3/2=750x1.5=1125 (notice this is the SDC, & L for G/Y-F Major)

Red-C Major 750 x 2/3=750x0.667=500 = BlueGreen/Green-G Major

BlueGreen/Green-G Major 500 x 3/2=500x1.5=750= Red-C Major

BlueGreen/Green-G Major 500 x 2/3=750x0.667=334 (UV-not seen, L for R/O-O-D Major)

[or for color: take 334 x 2 = 668=Red/Orange-Orange of D Major]

go to Locator (L) of BlueGreen/Green-G Major=1000

L 1000 x3/2=1500

L 1000 x2/3=667=Red/Orange-Orange-D Major

Red/Orange-Orange-D Major 667 x 1.5=1000 (SDC, & L for BG/BG/G-G Major)

Red/Orange-Orange-D Major 667x 0.667=445=Cyan-A Major

Cyan-A Major 445 x 1.5=667 =Red/Orange-Orange-D Major

Cyan-A Major 445 x 0.667=297 (UV-not seen)

[or for color: take 297 x 2 = 594=Orange-Yellow/Yellow-E Major]

go to Locator (L) of Cyan-A Major 445=900

L 900 x3/2=1350

L 900 x2/3=600=Orange-Yellow/Yellow-E Major

Orange-Yellow/Yellow-E Major 600 x 1.5=900 (IR not seen, SDC, & L for Cyan-A Major)

Orange-Yellow/Yellow-E Major 600 x 0.667=400=Violet-Purple-B Major

Violet-Purple-B Major 400 x 1.5=600=Orange-Yellow/Yellow-E Major

Violet-Purple-B Major 400 x 0.667=267 (UV-not seen)

[or for color: take 267 x 2 = 534=Green-F^#/G^b Major]

go to Locator (L) of Violet-Purple-B Major 400=800

L 800 x3/2=1200

L 800 x2/3=534=Green-F^#/G^b Major

Green-F^#/G^b Major 534 x 1.5=801 (IR not seen, SDC, & L for Violet-Purple-B Major)

Green-F^#/G^b Major 534 x 0.667=356 (UV-not seen, L for R-R/O-C^#/D^b Major -not shown)

[or for color: take 356 x 2 = 712= Red-Red/Orange-C^#/D^b Major]

go to Locator (L) of Green-F^#/G^b Major 534=1059

L 1059 x3/2=1589

L 1059 x2/3=706= Red-Red/Orange-C^#/D^b Major

Red-Red/Orange-C^#/D^b Major 706 x 1.5=1059 (IR not seen, L for Green-F^#/G^b Major)

Red-Red/Orange-C^#/D^b Major 706 x0.667=471=Cyan/BlueGreen-G^#/A^b Major

Cyan/BlueGreen-G^#/A^b Major 471 x 1.5=706= R-R/O-C^#/D^b Major

Cyan/BlueGreen-G^#/A^b Major 471 x 0.667=314 (UV-, L for O-O/Y-D^#/E^b Major -not shown)

[or for color: take 314 x 2 = 628= Orange-Orange/Yellow-D^#/E^b Major]

go to Locator (L) of Cyan/BlueGreen-G^#/A^b Major 471=948

L 948 x3/2=1422

L 948 x2/3=632= Orange-Orange/Yellow-D^#/E^b Major

Orange-Orange/Yellow-D^#/E^b Major 632 x1.5=948 (IR not seen, L for C-BG-G^#/A^b Major)

Orange-Orange/Yellow-D^#/E^b Major 632 x 0.667=422=Blue-BlueViolet-A^#/B^b Major

Blue-BlueViolet-A^#/B^b Major 422 x 1.5=633= Orange-Orange/Yellow-D^#/E^b Major

Blue-BlueViolet-A^#/B^b Major 422 x 0.667=281

[or for color: take 281 x 2 = 562= Green/Yellow-F Major]

go to Locator (L) of Blue-BlueViolet-A^#/B^b Major 422=841

L 841 x3/2=1261

L 841 x2/3=561= Green/Yellow-F Major

Green/Yellow-F Major 561 x 1.5 =841 (IR not seen, L for B-BV-A^#/B^b Major)

Green/Yellow-F Major 561 x 0.667=374 (UV-not seen, L for Red-C Major)

[or for color: take 374 x 2 = 748=Red-C Major]

go to Locator (L) of Green/Yellow-F Major 561=1125

L 1125 x3/2=1687

L 1125 x2/3=750= Red-C Major

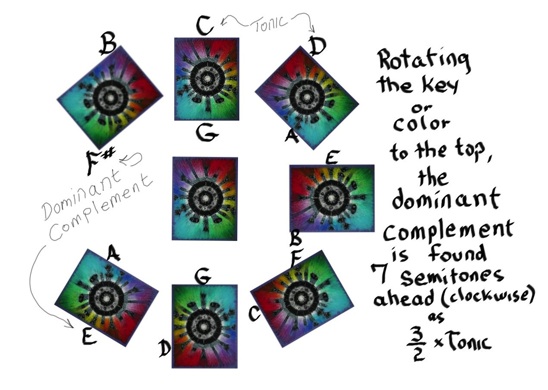
Fig. 11b. Rotating to the Tonic. When considering a music or color key as the tonic, one can calculate the dominant complement by multiplying / dividing its frequency / wavelength by the 3/2 ratio as described in various ways above this figure. One can also count the steps from the tonic to dominant…7 half-step semitones for music and 8 for color. In this figure, the actual music or color key is visually rotated to the top 12 o’clock tonic position and each respective dominant complement is marked below…in this example the musical key is designated. One can see the corresponding color. The complements are only directly opposite the wheel at the 6 o’clock position in one, and only one, situation…that when the tonic position is held by the Red-C Major key. Geometrically, when the 3/2 ratio is applied to generate the complement, they all look the same…symmetrical, with tonic and complement opposite. Visually, when the 3/2 ratio is reached by moving the required number of half-steps, they all look different…asymmetrical, with the tonic and dominant complement in different positions. Click HERE to enlarge image.

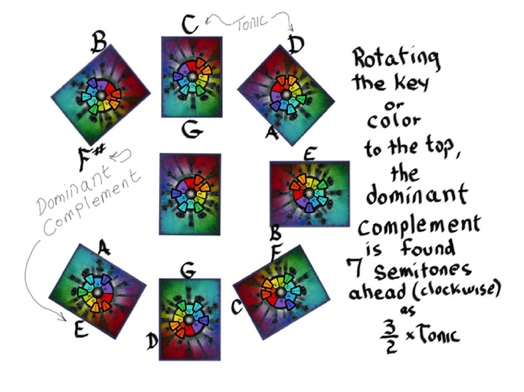
Fig. 11c. Rotating to the Tonic with the Piano Keys. Same information as above only now with the piano keys (in color) wrapped around the circles, with the tonic key always on top.Click HERE to enlarge image.

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

2.3 Premise 3...Structure and the ISL

The structural basis of both the atom, and subsequently, through the Golden Rectangle, the double helix of DNA, is defined by the ISL.

Not only does the ISL define the commensurate relationship of sound, color and light as well as the fundamental relationship between distance and the amount of gravitational and EM force between any two objects (matter/energy) in the entire universe, it also defines the structure of the atom.

The harmony of music and color is not simply a subjective phenomenon; it is inherently built into the very structure of the universe. It's no wonder that if atomic structure is built around the ISL, than so too must its fundamental forces of gravity and electromagnetism...and that the physics of sound and light and color should also be integrally determined by the same physical laws. Perhaps it's no wonder that sentient beings should develop a natural "subjective" affinity for certain sounds and colors that we “feel” are harmonious, complementary and "right" to us.

In a nutshell, the ISL informs atomic structure as such. In its simplest form, a positive proton and a negative electron form a unit called an atom. The electron is attracted to the proton, but maintains a minimum orbital distance from the proton because of the velocity of its orbital motion (which is itself explained fundamentally by the quantization of the orbital into whole-wavelength multiplies) produces an effective outward force that exactly balances its inward electromagnetic force. A situation that is analogous to the gravitational force. In both cases the relationship between the distance and the force of attraction between the two bodies of matter is defined by the ISL. By adding more protons (and electrically neutral neutrons) to the nucleus, more electrons are allowed in the orbital clouds.

Each orbital cloud layer (configuration) has a definite set of "rules" (quantum number states) defining precisely the number, disposition and energy of each electron. Each electron has two possible spin states, allowing two electrons (one for each spin state) for each of these orbital states within its orbital cloud. The closest orbital cloud (referred to as principle quantum state, n=l) is called the "s orbital" and contains two electrons.

The next orbital cloud (n=2) contains a second larger "s orbital," and a new "p orbital" which contains positions available for three electrons. Since all electrons come in one of two possible (but symmetrically opposite) spin states, there are two electron slots available for each of those three electron positions.

The third orbital cloud (n=3) contains a third larger "s orbital," a second larger "p orbital" and a new "d orbital," the latter of which contains positions for five electrons, or 10 electron slots.

The fourth orbital cloud (n=4) contains a fourth larger "s orbital," a third larger "p orbital," a second larger "d orbital" and a new "f orbital," with positions for seven electrons (times two spin states each), and so on. See Fig. 12.

Fig. 12. The ISL and the structure of the atom. Each s, p, d and f orbital increases in electron positions available and number of electrons, as well as distance from the nucleus and energy (inversely), as shown. The principle quantum numbers then describe how Nature builds up the structure of the atom in following the order of the odd number summation series: 1, 1+3=4, 1+3+5=9, 1+3+5+7=16... In the upper half of the image, the ideal order of electron shell filling for each quantum state, n, does so in a manner that is increased by 1, 3, 5, 7, times 2, electrons (as shown on the right), while the actual filling sequence follows the wavy arrow path. The spin states correspond to the standing wave-states of de Broglie. Click HERE to enlarge image.

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

2. DEVELOPMENT

A further relationship between the geometry of the ISL, music, art and structure will be briefly elaborated upon in their connection to the well-known Golden Rectangle (GR).

Consistent with classical Greek thought on ideal proportion, commensurability and harmony in music was a similar concern in the visual realm... sculpture, painting, architecture, pottery, and so on. Commensurate in thought and in presentation. Perhaps it is geometry which best characterizes the Greek mind, the Greek ideal... distillation of the germinal idea in its purest and simplest form...every space has a multitude of temporal possibilities but only a certain few of those possibilities best define the essence of that space...ideal proportion and commensurability is everything. Geometry presents the confluence of abstraction and manifestation.

One of their most influential geometric abstractions (not to be labored here) is the Golden Mean (Golden Section):

a : b = b/(a + b)

This ideal proportion is one in which the root (a) is increased to a degree (b), the sum of which (a + b), equals the inverse ratio of the root (I/a) to its movement root squared (b), or:

a + b = b/(a : b) = b/(a/b) = b²/a

where a = 1.0, b = 0.618 and a + b = 1.618.

In other words, despite claims that Greek thought centered around static space and static time geometry, the seminal ideal proportion is one of dynamic, commensurate growth.

The Golden Mean ratio provides harmonious growth in that every subsequent incremental growth in size is strictly related to its relative root that preceded it. When applied to plane geometry, they came up with the now familiar Golden Rectangle (GR), also known as the Whirling Squares (WS). A rectangle based on the Golden Mean (GM) proportions will generate a series of decreasing size squares whose diagonal (or arcs), when connected, will form a spiral...a spiral shape growth curve which abounds throughout Nature. It is called Dynamic Symmetry.

Art also abounds with the influence of this pivotal ideal proportion as well illustrated by numerous authors. What has not been presented or illustrated until now is the following.

3.1 ISL and the GR in Music and Art

The Circle of Fifths relates the major and minor key relationships. The outer circle shows the major keys progressively a Perfect 5^th apart, while the inner circle shows the corresponding minor keys. Forming a triangle around the desired key as shown in Figs. 13a and 14 below can show the diatonic triads for any key, major or minor.

Fig.13a. The Circle of Fifths, with an example in the key of C Major.

Immediately below the piano keys at the top, the key of C Major diatonic scale is laid out. Below that is the key of G (its DC) and F (its SDC)...all of which follow a pattern, left to right. of 3:2:3 Fibonacci numbers reflecting the Golden Mean. At the bottom right, the key of A minor shows a similar pattern. Within every Major key is its corresponding minor key, a minor third below...thus A minor uses the same semitones as C Major. In the circle of 5^ths, shown in the lower left, the triangle reveals the SDC, T, and DC on the outside, and its minor key...a minor third below, on the inside. Looking to the lower right on to a C Major reference circle, one finds that connecting lines, starting with the SDC F, between successive Perfect 5^ths, up to B, generates a 5-point star pattern. Continuing from B back to F by the sequence of Perfect 5ths forms a second 5-point star pattern. Pentagons are intimately related to the Golden Mean and Golden Rectangle, and, as we can see from the filled out chart in which each successive Major key (transposed Perfect 5^ths) on the left follows the 3:2:3 pattern...that is, located between the 3 leading semitones (1st, 2nd, and 3rd) and the 3 trailing semitones (6th, 7th and octave). A similar pattern occurs for the related minor keys that begin at the M 6th position within the Major diatonic scale. When combined into a Major-to-minor sequence...or one full line across of 13 semitones...the minor diatonic scale takes 8/13^ths on the right, the Major scale 8/13^ths on the left.. Click HERE to enlarge image.

Key modulations and chord progressions can be followed and interrelated in the Circle of Fifths. The Circle of Fifths informs, even defines, the architecture of the most advanced forms of occidental music. The diatonic major and minor scales inform the Circle of Fifths. Major and minor triads inform the diatonic scales. Simple ratio divisions of the M inform those triads and it is those divisions of the M, identical to those of the ISL, which ultimately defines that foundation.

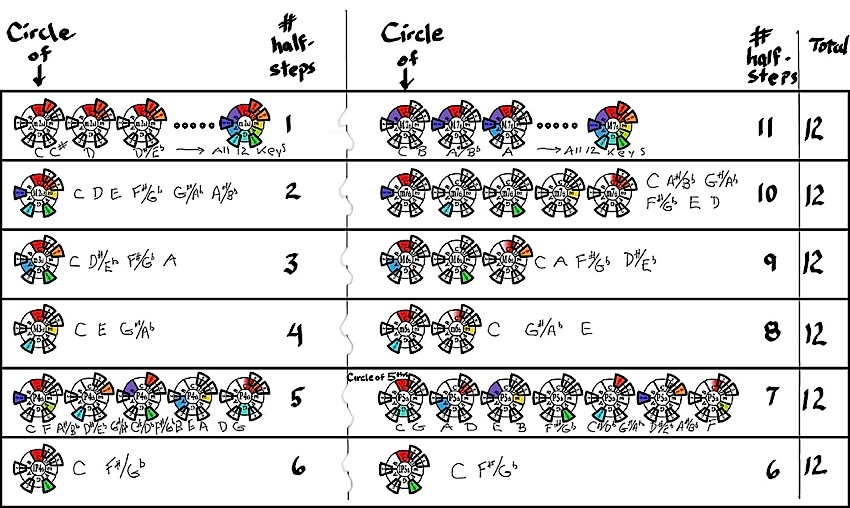
Fig.13b. The Circle of Second, Thirds, Fourth, Fifths, Sixths and Sevenths, with an example in the key of C Major.

With reference back to Fig. 11c, here we show how dividing up the octave by a certain fixed number of half-steps (semitones) unveils some common relationships between the keys. In each row, the key of C Major...at the tonic position on top...reveals the keys that are activated by moving forward along the scale the set number of half-steps indicated. The rows on the left directly relate to the rows across from them on the right...their number of half-steps always adds up to 12, the number of keys in the chromatic scale. They also contain the same activated keys only the order is reversed in one over the other. The completion of the octave to C² is implied but not shown the same. If the half-step progression moves beyond the keys found in the first octave, a second circular-piano key image appears and so on as octaves are required. In this case, the Red-C² key is shown as a bi-color...on the left side it remains white (inactive) as the half-step sequence must first pass past it around one more time to finish at C² with red on the right side. One can see that dividing the 12 tones by 1,2,3,4 or 6 half-steps simply returns one to the octave position...and while interesting, nevertheless either misses a tone or...as in the first row...simply runs the scale sequentially. Their mirror twin on the right accepts the same fate (in reverse). It is only by the division of 12 by either 5 or 7 half-steps that results in all 12 tones being activated before returning to the octave. Five half-steps from the tonic gives F, the Perfect 4^th. Seven half-steps gives G, the Perfect 5^th. In that the Circle of 4^ths presents the keys in reverse order...and is itself simply 7 half-steps down, or back, from the octave...the Circle of 5^ths becomes the pride and prejudice of key relationships. Click HERE to enlarge image.

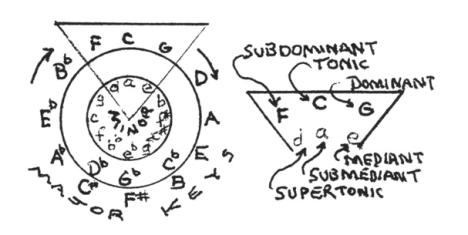
Fig.14. The Circle of Fifths, with an example in the key of C Major. Detail.

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

The Golden Mean is a natural consequence of adding two numbers together and the sum is than added to the larger of the previously added numbers:

Now, if the Golden Mean is applied to the 13 semitones of the chromatic scale or the 8 tones of the diatonic scale (both scales are octave to octave), one finds it to intersect the Perfect 5^th for any key selected, such that the Perfect 5^th always corresponds to the diagonal point of the Whirling Square, as shown in Fig. 15a-f.

There are 12 half step intervals between the octaves, with 7 half steps between the tonic and the dominant, defining the Perfect 5^th (complement) as the eighth note in the chromatic scale (thus 13/8=1.625), and the fifth note in the diatonic scale (thus 8/5=1.6).

Note from above that the Golden Mean of 1.618 is only approximated in the early, small numbers in this progression. Further to note, is that we are showing a dynamic of many squares inside of many overlapping WS. This is key to understanding the significance of this geometric growth progression. Each new part is made up of part of its past. The span of 13 semitones in going from C¹ to C² covers the whole, larger rectangle,

with its Perfect 5^th (G) covering the diagonal of its side forming the larger square in this rectangle.

However, when this same G later becomes the new tonic for the next sequence in this progression, the new proportions for its intervals are now defined by the new rectangle and new square formed of its new diagonal; thus when the two are combined one sees that the original 13 semitones now span an increasingly smaller space. The same occurs for the 8 semitones of the diatonic scale. Each new Whirling Rectangle (Square) is superimposed over part of the previous rectangle, masking the span were that rectangle left alone.

It is important that the interconnections between the ISL and sound physics, the ISL and light physics, the ISL and atomic physics (including structure, gravity and EM), and ISL and biologic structure (next topic) are emphasized, especially as we have now shown, through our music theory analysis, that a relationship also exists between the ISL and the GR.

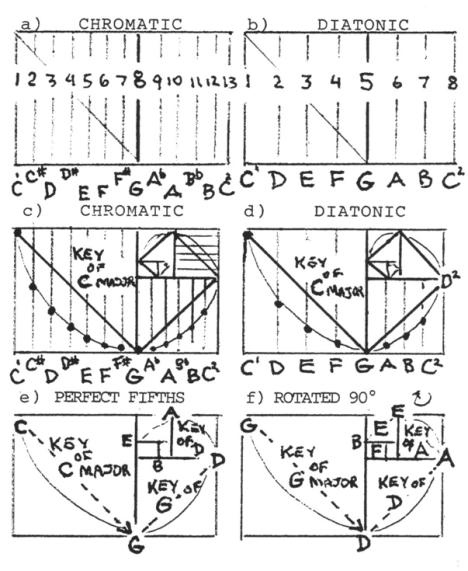
Figs. 15a-f. Chromatic and diatonic notes in the key of C are first shown in full span across the GR (a, b) with the DC G (the Perfect 5^th) at the diagonal to the square, and from this the same notes are assigned to the diagonal arcs of the Whirling Square (c. d). Further assignment of the successive Perfect 5^ths from the Circle of Fifths to each successive diagonal point of the diminishing Whirling Squares contained within the GR (e) corresponds perfectly with rotating 90°, such that now G is viewed as the new tonic, key, with the key of D, its dominant Perfect 5^th (complement), positioned at the diagonal point (f). And so it goes, each square becomes a new tonic key with its dominant and subdominant complements, following the Circle of Fifths, located at the two diagonals leading away from it.

The 12 Perfect 5^ths of the 12 keys of the major scales spiral in (counterclockwise) at repeating interval patterns of l:l:l:½:l:l:l:½:l... semitones, while the corresponding 12 Perfect 5^ths of the minor scales spiral out (clockwise) at repeating interval patterns of 1:1:½:1:1:½:1.... Figs. 16-18.

The GR has for thousands of years provided an ideal template to shape 2D and 3D form with its simple Nature-derived proportions. This template is related to an even larger template, the ISL.

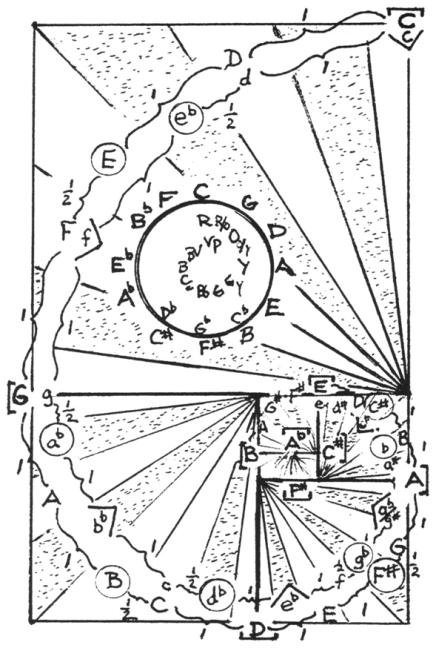
Fig. 16. Musical Whirling Squares. Twelve outer major keys spiral inward, twelve inner minor keys spiral outward while being read by the Circle of 5t^hs Color Wheel. (Based on a painting by the author, Simultaneous Birth of the Circle of Fifths and the Color Wheel, ©1987, R. Brooks.)

Fig. 17. Musical Whirling Squares. Twelve outer major keys spiral inward, twelve inner minor keys spiral outward while being read by the Circle of 5t^hs Color Wheel. (Based on a painting by the author, Simultaneous Birth of the Circle of Fifths and the Color Wheel, ©1987, R. Brooks.) Click HERE to enlarge image.

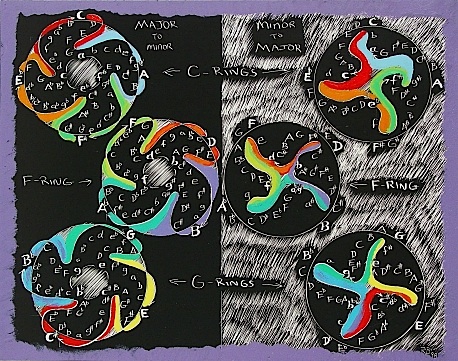
Fig. 18. Major-minor and minor-Major Ring Series.

Three ring patterns are formed in going from Major to minor (on the left) or minor to Major (on the right) starting with any 3 successive keys from the Circle of 5t^hs. Thus the first key ring F (SDC), the tonic key ring of C, and the DC key ring of G are each formed, respectively, from every 3rd Perfect 5th selected from the Circle of 5^ths. Each ring incorporates 4 Major keys (and thus forms a square within the Circle of 5ths), but it also incorporates its 4 related minor keys in forming either the Major-minor or the minor-Major scale. For example the C ring starts:

C Major - a minor - A Major - f^# minor - F^# Major - e^b minor - E^b Major - c minor - C Major

going clockwise for the M-m ring, and counterclockwise for the m-M ring as:

a minor - A Major - f# minor - F^# Major - e^b minor - E^b Major - c minor - C Major -a minor

Thus there is a second inherent geometry in the Circle of 5^ths...the first being its fundamental relationship based on 5’s, pentagons and the GR...and now we can see that the Circle of 5^ths can be deconstructed into thirds, that is, into 3 four-part rings (or squares if you like), each ring of which can be identified by the triangle around any three successive Perfect 5^ths on the Circle...but ultimately identified as the Tonic key of C, Subdominant key of F and Dominant key of G. Click HERE to enlarge image.

3.2 ISL and GR in Biologic Structure (DNA)

At the risk of overkill, the final link between physics, mathematics, chemistry and us...that is between structure, presentation and perception... is biology. The double helical structure of DNA reveals, when a composite image, end-viewed down its axis, of one 360° spiral rotation, it to be made of a series of concentric, double pentagon patterns...a 10 point design symmetrical about the center (except for the center itself which carries the variable code bases). The pentagon is completely and exquisitely defined by the GR (the topic of a recent, separate paper by the author, Patterns in Numbers...from Primes to DNA, c 1997, R. Brooks) like the Whirling Squares, has that property essential for the survival of life...the property of self-generation. Fig. 19.

Pattern In Number

from Primes to DNA

(starting with the Inverse Square Law)

NUMBER PATTERNS IN DNA

(GoDNA)

[This part of the paper has been extracted out, updated and adapted to the web under a separate title: GoDNA: The Geometry of DNA (axial view), in order to give this marvelous, magical molecule of Nature its own proper due. Please visit the link above and return to this same spot by the link back (or use your "back" button).]

STRUCTURE & CHEMISTRY OF DNA

(SCoDNA)

[ The main section of the Number Patterns in DNA has been given its own title, GoDNA: The Geometry of DNA , and a separate section to go to view this work. This section, has also been extracted from Patterns In Number (PIN), reworked and adapted for the web as: SCoDNA: The Structure & Chemistry of DNA (axial view). It builds on the foundation laid down in GoDNA. It is for those who wish to get deep into the design (and chemistry) of the DNA double helix as presented in the composite axial view. Others may want to skip this section altogether but I do hope you will peruse GoDNA to see first hand the marvelous number magic and pattern. For those who are digging in, you will need to access GoDNA and the Figures and Tables contained within, to proceed from here.]

Fig. 19. Composite axial view of one 360° rotation of the DNA double helix reveals a striking 10-point pattern composed of a series of concentric double pentagons (decagons) that are intimately defined by Golden Mean ratios of the GR and ISL.

A couple of examples of the axial view of 360° rotation composite of DNA double helix graphic by author are shown below, Figs 20 and 21. Dozens more can be found HERE.

Fig. 20. Axial view of 360° rotation composite of DNA double helix graphic.

Fig. 21. Axial view of 360° rotation composite of DNA double helix graphic.

Opposing that grand second law of thermodynamics, that law which establishes an arrow of time which ultimately sucks all life, all pattern, all order out of the universe is the anti-entropic force of organization fueled by forces of attraction (and repulsion) and self-replication (self-generation) which is mysteriously informed by mathematics, especially that which we know as geometry. More than likely, geometry informs it all, order and chaos. That geometry as an abstract can generate and reproduce itself, maintain and/or "grow" in proportion to its past, its present and its future spacetime constraints is beautiful. That it can also manifest itself as the organizing force behind the forces of gravity and electromagnetism (and undoubtedly the strong and weak nuclear forces)...that it can inform and define the structure of the atom, the structure of DNA...of life itself, including our perceptions and responses to much of that life, of that universe, especially to that which we elevate to our highest standards of existence, our expressions of who we are...our Art, our Science and our Culture...is what Einstein called the greatest beauty of all...the mystery.

Phylogeny recapitulates ontogeny recapitulates geometry.

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

CONCLUSION

Delacroix described art as the communication between two souls. Picasso said art is a lie that reveals a truth. While progress in science has been enhanced by the rigorous pruning of unwanted and irrelevant grafting of religion, politics, and yes even of esthetics, the polarization of art and science is in the end the ultimate injustice to both.

Science and art are both constructs of the human mind trying to comprehend and communicate the essence of our existence. It is so very exciting to see logic, creativity, color, mathematics, music, physics and art pulling together to meet such lofty goals.

Nature's game plan for sound allows us to hear music and other pleasing sounds when the natural harmonics of vibration are present. When the music is interesting and communicates something beyond those harmonics we call it art.

For sight. Nature's game plan of color allows us to see beautiful and pleasing colors when the natural harmonics of color vibration are present. Again, we call it art when we bring together some color sensation which goes beyond technique.

Although we, as part of Nature, require art to survive.. .to form an emotive and intellectual basis upon which to expand, even justify our consciousness...Nature is pragmatic.

It is interesting that the first harmonic of a given color (ie., the complement) should neutralize the color, while in music the first harmonic (the Perfect 5^th ) generally enhances the richness of the sound. In the visual world, warm lights generate cool shadows and vice versa. Life colors itself with complementary colors... often as: the tonic color-gray-the dominant complementary.

The primary office of color is to distinguish... self from non-self ...edge from surface... flat from round...object from object...matter from light... light from shade...foreground from background... sickness from health...and so on. In most all these situations, the complementary color or effect (through mixing) allows us a further refinement in our ability to distinguish. That every wavelength of the EM spectrum has a double complementary relationship with two other wavelengths suggests Nature's game plan for vibrational field phenomena far exceeds the little discoveries we have found in mixing a few colors. The harnessing and use of light energy may be enhanced and controlled by focusing on this new complement relationship. That the ISL should define the field effects of gravity, EM, sound and light is actually not so much surprising, as inevitable.

Communication between the sciences, between science and art, but especially between individuals can be enhanced by the holistic presentation of Nature. Individuals will lock onto the signal they best appreciate and use that to springboard to better understanding.

If colors can be translated into sounds, if the complement of a color acts as a binary on/off switch, if the complement of a sound pitch can define a geometric shape, we have the basis for intercommunication between individuals (and machines) never before realized. Art will always remain the communication between souls that no machine can touch, but our tools for creating that art will surely evolve to encompass all that science and art together can bring forth.

In every case where either the ISL or the Golden Rectangle comes into play...art, music or science...each implies the mathematical beauty of the other because both are similar, related and yet different ways of expressing one of Nature's most formidable laws...Nature is commensurate. The pentagon is completely defined by the Golden Rectangle. The Golden rectangle nicely accommodates the ISL as representing the successive fifths (complements) of each fundamental tone or color. We are and occasionally duly perceive our oneness with the universe...its perfect unity and unimaginable diversity based on the most exquisite variations on a theme. That the mathematics and geometry of the ISL and Golden Rectangle can be shown to provide a structural, presentational, perceptual and perhaps even esthetical basis for our physics, chemistry and biology of beings is both astounding and yet as we know more and more of Nature, absolutely destined. Nature is commensurate.

APPENDIX A

Oil paintings by the author that summarize some of the major relationships described in the paper. Visit www.brooksdesign-ps.net -->Portfolio for additional works.

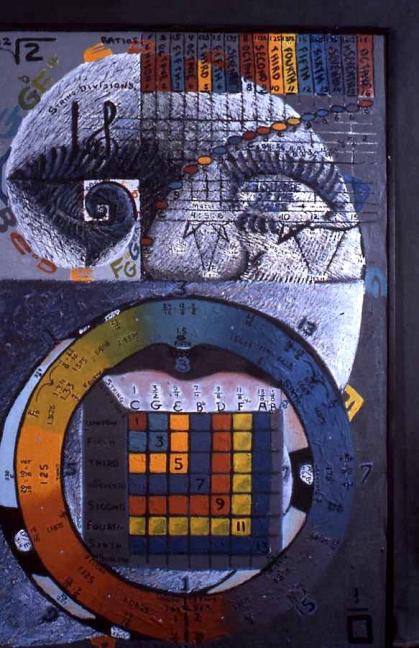
"Music, Color and The Inverse Square Law” (top)

"Simultaneous Birth of the Circle of Fifths and the Color Spectrum” (bottom), ©1987, Reginald Brooks. All rights reserved.

APPENDIX B

Expose

on

Music, Color and the Inverse Square Law (select parts presented)

Reginald Brooks

1987

Music, color and the inverse square law

Musical scales, the division of the monochord, the Pythagorean, just intonation, and equal temperament tunings and the circle of fifths (shown below), are looked at with the aid of color and geometry.

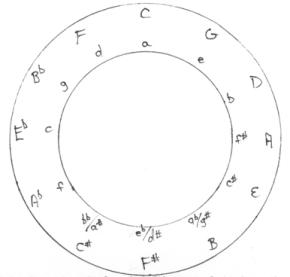
When the fifths from the circle of fifths are plotted as the whirling squares of the golden rectangle, the following result occurs starting with the key of C major, traveling counterclockwise each time to the next smaller square.

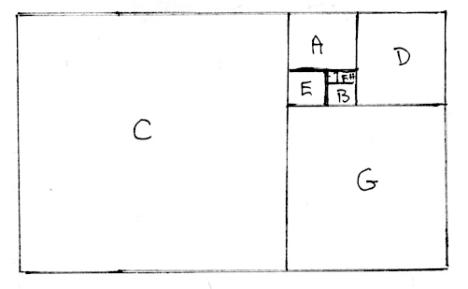
The squares of the above diagram represent the background of that tonic key.

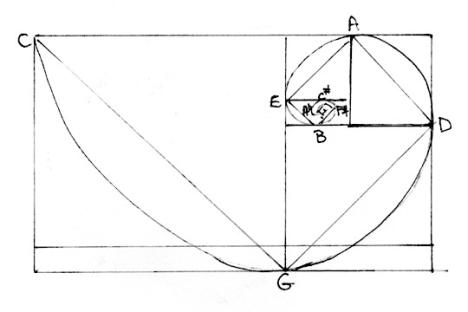
A diagonal line across the square to the next smaller square always points to its respective perfect fifth, and when the diagonals are smoothed out into curves a spiral form is developed, with the sequence of perfect fifths beginning each successive square. (Note in the painting of the "Simultaneous Birth of the Circle of Fifths and the Color Spectrum”, above, the spiral has been enlarged inwardly to accommodate the information.)

If the home tonic key of the major scale in question is placed at the beginning of the square and is designated by a square symbol, then placing a small circle around its respective major third establishes the tonic, dominant and subdominant triads for any given key starting at the beginning of its square.

Adding the appropriate keys in between and designating the size of the interval steps of the major scale form the basis of the next two diagrams.

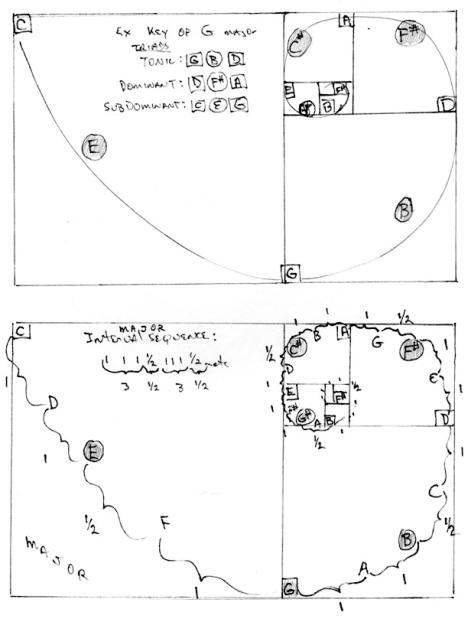
Note that the interval pattern of the major scale follows as:

3 whole steps--½ step-3 whole steps--½ step and so on.

The natural minor scale, to be shown, has an interval pattern of:

2 whole steps--½ step-2 whole steps--½ step and so on.

The harmonic and melodic minor scales have the same intervals at the beginning of the scales as the natural minor, out have different intervals at the end of the scale.

Because the major and minor keys share the same key signatures, the expression of the minor key requires that the minor triad (i.e., a short step interval) predominates in the frequency of the tonic home key, while the major triad (i.e., a long step interval) predominates in frequency of the tonic home key for the expression of a major key.

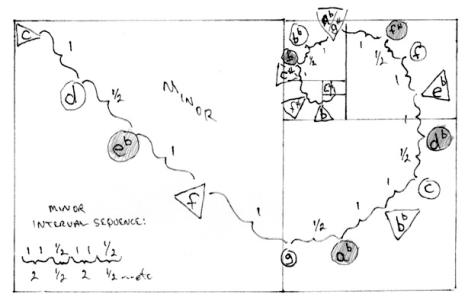
The natural minor key, unlike its related major key, does not have its perfect fifth at the beginning of each square. Each new key, a fourth above its predecessor key, is designated by a triangle, and while geometrically following the same counterclockwise direction as the major scale in the circle of fifths, the sequence of the circle of fifths of

the minor key travels in the opposite direction (clockwise) to that of the major scale. In effect the major scale spirals in and the minor scale spirals out.

In the outer major scale, the major third of the tonic triad is circled and shaded. In the inner minor scale, the minor third of its tonic triad is also circled and shaded. The perfect fifth of that respective minor key is designated by the next non-shaded, circled key following the shaded, circle key of its minor third (and the next new tonic key). Combining the two, major and minor, together and placing in the piano keys into the background give the "birth of the circle of fifths."

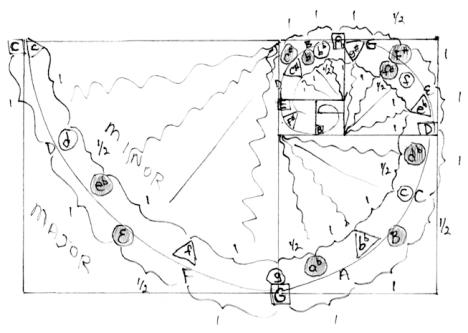
Some of the complexities of color can be simplified, by treating the color spectrum as an octave, whose complementary color (additive color) is positioned in the same geometric space as the perfect fifth is for its tonic within its octave. Color constancy, especially as elucidated by Edwin Land, is key to the human perception of color. Color constancy is the same color perception under widely differing lighting (and thus energy) conditions.

The mind looks at the whole visual field of a particular energy, compares the energy differences at the various borders within the field, and from this computes that, within this energy context, this is a red, that a green, that a blue and so on. The mind applies a spectrum, an octave, across the energy field it has perceived, and assigns color (pitch) to each area of energy (frequency) relative to that field.

Now change the energy field by either going to a higher or lower octave, or by centering in between on a different key and the mind recomputes the color. But, alas, while it recognizes the tonic of whatever key, it also recognizes that E is not D, F, G, A, B or C, and likewise, that red is not green, blue or yellow. Trees that are green in winter remain green in summer.

Unlike the ear, the eye does contain receptors somewhat specific for certain classes of wavelengths (colors) of light and it is apparently by matching up the relative amounts of stimulation of the red, green and blue cones for any given visual field that the color constancy is maintained. In quantum physics, space and time, as rulers and clocks, are very definitely relative to the energy field in which they reside, and in a somewhat analogous, and even paradoxical, manner color which traditionally has been given the office of differentiation, to point out differences amongst similarities, has now been shown to provide a kind of visual constancy, or sameness, within the relatively small, but rapidly changing energy fields that occur on earth. So that within any octave of color field vision, red will be perceived as red as long as enough relatively long wavelength photons are present to stimulate the red sensitive cones relative to the overall energy field perceived by comparing the field seen by each of the three color sensitive cones. Saturating the color field with blue-green light will of course override the sensation of red, much as persistent modulation to a new key will negate the old key unless the original, home key is re-established.

The circle of fifths has been reinterpreted in geometric terms, forming the areas of the golden rectangle. The spiral inscribed into these areas has two poles: it defines the notes of each key of the musical scales and it defines a full color spectrum within each key. The outer section of the spiral defines the 12 major keys, the inner section the 12 minor keys. Color-pitch consistency is maintained throughout.

C is always red, its fifth, G, is always blue-green (its compliment, both musically and spectrally, additive color).

E, the third interval from C, is always yellow, F, the fourth, is yellow-green, etc.

The background square of that part of the spiral in which it sits is colored according to the tonic key (reading from the larger square to the smaller squares). Thus, the key

of b (first square) is red. In addition, the background square may be thought of as a keyboard with the color portion representing the white keys and the black squiggly lines the black keys (sharps and flats). Following the spiral, the background square always ends at the perfect fifth of that major key, and the key of C has a red square background which ends at G, the perfect fifth of C.

Now, starting with the key of G, whose perfect fifth is D, the background square is the blue-green of b.

The next circle of fifths key is D, whose background of orange ends at its perfect fifth of A, and so on.

Minor keys on the inside of the spiral start at each triangle. The tonic, subdominant and dominant triads as well as numerous other key modulation and interval relationships are delineated and/or suggested. The interrelationship of complimentary colors to compliment pitches (sounds) is clearly demonstrated.

©1987, Reginald Brooks. All rights reserved.

Newer version. Copyright ©1998, Reginald Brooks. All rights reserved.

REFERENCES

Homer, W.I., 1964, SEURAT and the Science of Painting, The M.I.T. Press, Cambridge, MA,, USA.

M Hose, A.I.,1951, Basic Principles of the Technique of 18^th and 19^th Century Composition, Eastman School of Music, Appleton-Century-Crofts, Inc., New York, NY, USA.

Land, E.H., 1959, "Experiments in Color Vision," Scientific American, 200:38, May, pp. 84-94.

Note: This paper draws from the three earlier papers (all stages in the evolution of this work) below, as well as from my “Artist Statement” that accompanied showing parts of this work, including paintings, at the Montage Gallery, Portland, OR, in 1996.

"The Geometry of Music, Art and Structure: Linking Science, Art, and Esthetics," was presented by the author at the 8^th ICECGDG (International Conference on Engineering Design Graphics and Descriptive Geometry, sponsored by the International Society for Geometry and Graphics, the Japan Society for Graphic Science, and the Engineering Design Graphics Division of the American Society for Engineering Education; hosted by the College of Engineering, The University of Texas at Austin).1998.

Published in the Proceedings of the 8^th ICECGDG, Vol. 2, pg 378, ISGG, Tokyo, Japan, 1998. A number of the graphics presented have since been redone and/or expanded upon and, along with new works, are now included for the first time in this collected work.

Brooks, Reginald, 1987, “Expose on Music, Color and the Inverse Square Law” (select parts presented), pp 2-7. (See appendix.)

Brooks, Reginald, 1995-96, “The Geometry of Music, Art, and Structure ...linking Science, Art and Esthetics” (select parts presented), pp 1-38.

Brooks, Reginald, 1998, “The Geometry of Music, Art, and Structure: Linking Science, Art, and Esthetics” (select parts presented), pp 1-12.

---

This paper and all its contents © 2009, Reginald Brooks. All rights reserved. Permission is hereby granted for single copies to be made for personal, non-commercial use for students and teachers of schools, colleges and universities provided that: either the entire paper, including figures and tables, is kept intact; or, any extracts of the text, or figures or tables (in part or whole), be properly and visibly cited as to authorship and source.

---

MUST SEE: A new media... and interactive... net.art project netart07: Geometry of Music Color utilizes and greatly expands upon the graphics and music theory presented in this white paper. Included are several "Color Music Composer" interactive pages for the music/color composer within us all!

Click here for the "The Geometry of Music And Color, GoMAC, parts II and III" (added 05/25/2012)

________________________________________________________

GoMAS

---

---

---

---

Page 2a- PIN: Pattern in Number...from primes to DNA.

Page 2b- PIN: Butterfly Primes...let the beauty seep in..

Page 2c- PIN: Butterfly Prime Directive...metamorphosis.

Page 2d- PIN: Butterfly Prime Determinant Number Array (DNA) ~conspicuous abstinence~.

Page 3- GoDNA: the Geometry of DNA (axial view) revealed.

Page 4- SCoDNA: the Structure and Chemistry of DNA (axial view).

Page 5a- Dark-Dark-Light: Dark Matter = Dark Energy

Page 5b- The History of the Universe in Scalar Graphics

Page 5c- The History of the Universe_update: The Big Void

Page 6a- Geometry- Layout

Page 6b- Geometry- Space Or Time Area (SOTA)

Page 6c- Geometry- Space-Time Interactional Dimensions(STID)

Page 6d- Distillation of SI units into ST dimensions

Page 6e- Distillation of SI quantities into ST dimensions

Page 7- The LUFE Matrix Supplement: Examples and Proofs: Introduction-Layout & Rules

Page 7c- The LUFE Matrix Supplement: References

Page 8a- The LUFE Matrix: Infinite Dimensions

Page 9- The LUFE Matrix:E=mc²

Page 10- Quantum Gravity ...by the book

Page 11- Conservation of SpaceTime

Page 12- LUFE: The Layman's Unified Field Expose`

Page 13- GoMAS: The Geometry of Music, Art and Structure ...linking science, art and esthetics. Part I

Page 14- The Geometry of Music And Color, GoMAC, parts II and III" (Brief visual overview of GoMAS)  

Page 15- Brooks (Base) Square (BS): The Architecture of Space-Time (TAOST) and The Conspicuous Absence of Primes (TCAOP) - a brief introduction to the series

Page 16- Brooks (Base) Square interactive (BBSi) matrix: Part I "BASICS"- a step by step, multi-media interactive

Page 17- The Architecture Of SpaceTime (TAOST) as defined by the Brooks (Base) Square matrix and the Inverse Square Law (ISL).

---

---

---

Copyright©2009-12 Reginald Brooks, BROOKS DESIGN. All Rights Reserved.

---

The LUFE Matrix | The LUFE Matrix Supplement | The LUFE Matrix: Infinite Dimensions | The LUFE Matrix: E=mc² | Dark Matter=Dark Energy | The History of the Universe in Scalar Graphics | The History of the Universe_update: The Big Void | Quantum Gravity ...by the book | Conservation of SpaceTime | LUFE |

net.art index | netart01: RealSurReal...aClone | netart02: funk'n DNA/Creation GoDNA | netart03: 9-11_remembered | netart04: Naughty Physics (a.k.a. The LUFE Matrix) | netart05: Your sFace or Mine? | netart06: Butterfly Primes | netart07: Geometry of Music Color | net.games | Art Theory 101 / White Papers Index