| art theory 101~The LUFE Matrix Supplement:
Examples & Proofs |
The LUFE Matrix Supplement: Examples and Proofs
The distillation of System International (SI) units into more fundamentally base units of Space-Time (ST) dimensions
Short Title: The LUFE Matrix Supplement
Copyright©
1985, 1991, 2003, Reginald Brooks. All rights reserved
Introduction-Layout & Rules-Page 7a
Contents
Introduction-Layout & Rules
page 7a
Index, Examples & Proofs
page 7b
References
page 7c
Introduction
This supplement is designed to accompany the "The LUFE Matrix: The distillation of SI units
into more fundamentally base units of space and time dimensions. The LUFE Matrix was
developed and published by the author originally in 1985 and
was subsequently presented in other papers culminating in the 1991-92 work from which the title
and substance of this digitized version is based.
Because the LUFE Matrix addresses the most fundamental units of physical expression, it is
concerned with all fields in physics, and many of those in pure mathematics.
Well over 200 examples and proofs are provided starting with the simple examples of classical
Newtonian mechanics. As the reader gains understanding and proficiency in using the matrix, the examples,
following in a very rough sense the historical development of physical thought, become ever
so challenging. However, once through the section on electromagnetism, one has become fully proficient
in applying the LUFE Matrix to the advanced fields of modern physics.
In a sense, the proof is in the pudding. the LUFE Matrix works in all
fields of physics in which the physical expression can be reduced to space-time (ST) dimensions.
The examples presented here not only reveal the operational rules of the matrix and some of
the suggested graphic representations of the matrix in action, they also prove their validity by
being invariant in all forms of physical thought expressed in System International (SI) consistent
mathematical form.
Thus mass, as SIII/TII (Three dimensional units of space per two dimensional units
of time) is valid as it is used in Newtonian mechanics, properties of matter, electromagnetism,
special and general relativity, quantum mechanics (including dense matter, plasma, and low
temperature physics), cosmology, particle physics, and quantum field theory.
The same for the other entities. The invariance of their ST designations throughout diverse
fields of physics supports their validity. any mathematical operation in which the essential effect
is to multiply or divide one or more entities (of SI derivation) can be restated on the
LUFE Matrix...and in simpler, more fundamentally base terms.
The conceptual simplicity that the LUFE Matrix allows in this ultimate distillation of
dimensional analysis far exceeds the minimal effort required to become proficient in its use.
Nature is multi-dimensional, maintaining an essentially perpendicular symmetry of space
to time dimensions in forming the matter and fields to which we ascribe a reality. The LUFE
Matrix is a new and original mathematical distillation of the fundamental units (and concepts)
which account account for physical law. Use it wisely, peacefully and harmoniously at all times.
Although some of the introductory layout material presented here is repeated, the
full account in The LUFE Matrix: Introduction-Layout should be reviewed for starters.
|
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
sidebar 1:
PREVIEW~~~~~~~~~~~~~~~~~~~~REVIEW
can you say "Energy" ten different ways
Slide Show
Quick & Simple Visual Overview
Recommended: Before & After
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
|
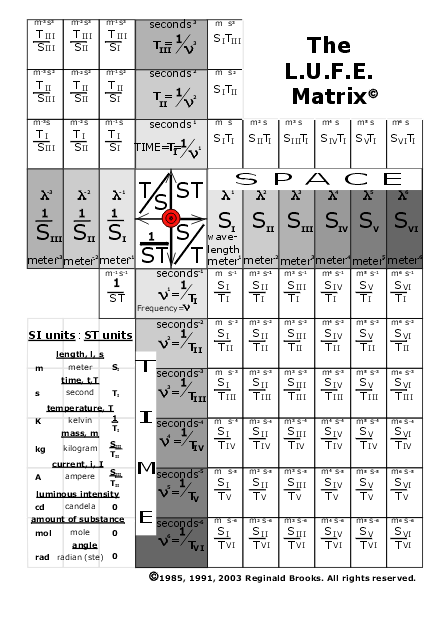
The LUFE Matrix Layout
We start with the familiar x-, y-axis of the Cartesian coordinate system in which four
quadrants are formed, designated as: ST, S/T, 1/(ST), and T/S, clockwise. More on this in a bit.
The horizontal x-axis designates the pure spatial dimensions:
Space (S) as SI, SII, SIII,…and so on.
The vertical y-axis designates the pure temporal dimensions:
Time (T) as TI, TII, TIII,…and so on.
From the origin, the spatial axis is positive to the right, negative to the left. The temporal
axis is positive up, negative down.
Some entities have purely spatial dimensions, e.g., displacement, length, radius, area, volume,
wavelength, etc. These are located on the horizontal "space" axis.
Some entities have purely temporal dimensions such as elapsed time or frequency, the two of
which are reciprocally related in that frequency is cycles per second. (The inverse of time,
T =1/T=n
= frequency.) These are located on the vertical "time" axis.
However, the vast majority of physical entities are expressed in the interactive ST
dimensions in which a combination of horizontal spatial dimension(s) and vertical temporal
dimension(s) gives the physical expression. This appears on the LUFE Matrix in one of the four
quadrants, usually in the S/T lower right quadrant as most entities have a net dimensional
expression of so many S dimensions per so many T dimensions. For example, the velocity of
light, c equals so much displacement per unit of time = meters per second = space/time
= S/T= wavelength (l
) times frequency (n
) = l
n
.
When an item is per something spatial, or per something temporal, that is effectively
dividing that item by the spatial or temporal dimension(s). Meters per second translate as m/s,
or positive space meters and negative time seconds on the LUFE Matrix. This would place velocity,
or m/s in the lower right quadrant as SI/TI (it is equivalent to placing
an item on the x-, y- coordinate system at x=+1, y=-1). Another common way of expressing division
of, or the denominator in a fraction, is with the negative exponential, i.e. m/s = m s-1
and m/s2 = m s-2, and so on.
That's it, that's just about as tough as it gets. We are going to refine this process and
lay down some "rules of the matrix", but the idea is no more complicated than this. To avoid
confusion of so much information, it is helpful to focus on the S/T quadrant realizing that the
whole matrix is symmetric.
Notice that we have used the word dimension in three ways: (a) as spatial dimension, S; (b)
as temporal dimension, T; and (c) as space-time dimension, ST. From the origin, the number of
spatial dimensions increases sequentially as SI, SII, SIII,…and
so on, each S unit represents one unit of spatial dimension.
And yes, while we can readily assign any one unit of S (SI) as linear space, and
two units of S (SII) as area, and any three units of S (SIII) as volume,
we must accept Nature's design in which four (SIV) and five (SV) or more
spatial dimensions are required.
The same for the temporal dimension, each increases sequentially out form the origin as 1/T
I, 1/TII, 1/TIII,…and so on. Here again, one unit of time may
be thought of as per second, and two units as per second second, or per second 2, and so on.
Each pure space or pure time dimension (i.e., SI, SII, SIII,…
and 1/TI, 1/TII, 1/TIII,…etc.) is to be thought of as extending
linearly to infinity (like a beam of light) and at a direction perpendicular to its axial
location. Thus SI extends vertically to infinity in both the positive and negative
direction and 1/TI extends horizontally to infinity in both the negative and positive
direction.
It is on the S/T quadrant of the matrix that the pure spatial and pure temporal dimensions
overlap…crossover…forming an area of ST, here as S/T, that defines dynamic, interactional ST
dimension. Here is where most of the physical entities express themselves. In the ongoing
example, the linear SI dimension dynamically interacts with the linear 1/TI
dimension to give the SI/TI area which designates the velocity of
light, c = SI/TI = meters/second = l
n
.
Although some of the introductory layout material presented here is repeated, the
full account in The LUFE Matrix: Introduction-Layout should be reviewed for starters.
The LUFE Matrix Operational Rules
- The area on the matrix defines the physical entity and its units of
expression.
Interactional ST dimensions have areas within a quadrant, while purely spatial
or temporal dimensions have linear "spaces" along their respective axis. The identity of a
physical entity, be it a quantity or the units to describe/measure it, in terms of net amounts
of so much spatial dimension and/or temporal dimension is constant and does not change regardless
of its operation location on the matrix.
- All net areas and spaces are counted from the origin, 0, where the x-(space) and
y-(time) axial coordinates cross
.
- Pure spatial (like length) or temporal (like time, frequency or temperature) dimensions
never appear by themselves in a quadrant.
They are confined to their static, linear
space on the axis. These are referred to as Space Or Time Areas (SOTA). Pure spatial
dimensions always go to infinity in both the up and down directions for each spatial dimension.
Pure temporal dimensions always go to infinity in both the left and right direction for each
temporal dimension. Each is like a bipolar laser.
- It is only in perpendicular combination(s) that space and time dimensions
dynamically interact to form ST interactional dimensions (STID).
- Once you are on the matrix proper, that is on the STID area, then the multiplication
(by addition) or division (by subtraction) of any other dimensions, be they ST interactional
dimensions or pure spatial or temporal dimensions, is begun from that area already defined
on the matrix at that point (not from the origin, 0), using its usual ST designation.
For example, acceleration (SI/TII) is velocity (SI/TI)
per unit of time (TI), so if velocity is first located on the matrix at the S
I/TI ST interactional area of the S/T quadrant, then dividing this per unit
of time (TI), which is the same as multiplying it by 1/TI, requires in this
case that we add one unit of pure temporal dimension (1/TI) to the existing S<
SUB>I/TI STID area to give acceleration (SI/TI
·
1/TI = SI/TII).
Tip: Get on the matrix proper first
with the larger STID areas, then combine the smaller STID units and/or pure
SOTA units. Remember to keep the distinction between SOTA and STID areas
clear in mind during all operations. Each is composed of pure dimensions that run to infinity,
but only STID areas have both space and time dimensions. Once we get into the
mathematical equations, all of which can be simplified and solved on the matrix, we will then
begin to add and/or subtract various SOTA and STID areas to others already on the
matrix. This entails building out (for multiplication we add areas) or in (for division we
subtract areas) as the equations are solved. SOTAs are added or subtracted to the grid
row or column, to which their bipolar, laser-light-like influence extends, thus they act next
to the sides of an existing area. On the other hand, STID areas are added or subtracted
diagonally to other STID areas. This is only natural as the STID areas have their
dual, perpendicular, bipolar, laser-light-like influence going both horizontally and vertically.
- Only physical entities that have net dimensional quantities appear on the
matrix or are involved in any of the operations of the matrix. Dimensionless units include any
pure numbers, integers, fractions, geometric ratios, radians, trigonomic, logarithmic, or other
functions, and the like.
In short, any units such that when their SI units are converted to
ST units and there remains no net ST units then such entities are dimensionless units. Examples
include Newton's gravitational constant, Coulomb's constant, the permittivity of free space, the
dielectric constant and the fine structure constant.
- The LUFE Matrix readily displays the dynamics of mathematical operations involving the
multiplication or division of physical entities. Addition or subtraction does not effect
the matrix, nor does the order in which mathematical operation take place.
It is only
the net, remaining area (or linear space) that counts.
- Multiplication in the matrix is akin to exponential multiplication…the product of two or
more dimensional quantities is found by the addition of their dimensional designations.
Two
examples: SI ·
SIV = SV, and, SI/TI ·
SIV/TIII = SV/TIV.
- Division is similar to exponential division…the quotient of two or more dimensional
quantities is found by the subtraction of their dimensional designations.
Two examples:
SV/TIV ¸
1/TI = SV/TIII, and (SIII/TII)
2 ¸
(SI)2 = SIV/TIV.
- The LUFE Matrix is equally valid for the MKS, CGS and other less universal systems of
units as the idea is to reduce and distill these systems to one in which there are only two
fundamental base units, space and time
.
The LUFE Matrix Graphic Dynamics
Digital version for the computer: grays-
inactive, color-active
Rules of engagement
In the following graphics, hover your cursor over the text and the graphic will
change to reflect that text. (You must allow the computer to load the images for the first
time, thereafter it will respond more quickly.)
(Please note: This area will be developed to specifically define how the working "examples & proofs"
will be presented graphically once they have been digitized. Any number of simple graphic means
to designate active and inactive areas, both net and operational, may be utilized. For nearly
20 years The LUFE Matrix has existed purely on paper with little more than outlines, parallel
and squiggly lines, and encircled text and symbols...all in black and white. Whatever system you
adopt to teach/learn from the matrix, it is most important to be consistent. The matrix is easy.)
- General-SOTA (Space OR Time Areas)
- ·Green-Horizontal-Time goes to infinity both ways
- ·Blue-Vertical-Space goes to infinity both ways
- General-STID (Space-Time Interactional Dimensions)
- ·Deep RGB
& O Color Blend-Boxes- go to infinity all 4 ways
- Division
- ·Squiggly Lines=Division (subtraction)-lines go to infinity
- ·Yellow-box Outlines=net area subtracted out
- Multiplication
- ·Parallel Lines=Multiplication (subtraction)-lines go to infinity
- ·Grayscale-box Outlines=specific ID area for that quantity added
- Net Areas (after operations)
- ·Bold Black Symbol=Net Area ID
- ·Bold Black-box Outline=Net Area after operations completed
- ·Deep RGB
& O Color Blend-Boxes-, or,
- ·Green-Horizontal-Time box, or
- ·Blue-Vertical-Space box, shows Net Area*
- ·PurpleDot=Diagonal Corner-of Net Area*
- Special Cases, i.e. Examples
- ·Various other Colored Dots=Diagonal Corners of specific ID areas & operations
- ·Large, complex layouts will have simplified graphics
*In order to graphically show several operations on a single diagram, not all of the STID Net Area
Colored Boxes will be shown so that the component ID's STID areas making up that Net Area will
be more easily visualized. Thus the Purple Dot. The Net Area is
always the greatest Diagonal Corner of that area and it is always marked to identify
it as so by both a STID Net Area Colored Box & a Purple Dot at that corner.
~hover your cursor over the highlighted text to show its matrix location~
Multiplication (addition) & Division (subtraction) Examples
~hover your cursor over the text on the right for images~
~click image for full matrix blowup~
~if needed, click and hold while you scroll~
|
|
~best viewed 800x600,
~toggle F11 for full image |
|
Graphic Examples
|
|
# |
description |
ST unit |
|
1 |
space axis |
- |
|
2 |
time axis added |
- |
|
3 |
axes in color |
- |
|
4 |
grid boxes added |
- |
|
5 |
text added to boxes |
- |
|
6 |
working color template |
- |
|
7 |
1-space dimension |
SI |
|
8 |
per 1-time D |
1/TI |
|
9 |
1-space/1-time =
c=velocity of light |
SI/TI |
|
10 |
2-space/2-time =
c2=velocity of light2 |
SII/TII |
|
11 |
Multiplication (addition) & Squares |
SV/TIV |
|
12 |
Division (subtraction)
& Square Root |
SI/TI |
| In #11 we start with mass, m, and diagonally add the velocity
of light, c, twice to give the energy, E. In #12 the reverse, we
start with the energy, E, and diagonally subtract out the velocity of light, c, twice.
The order does not matter, only the Net Area remaining. |
|
NEXT:
On to Page 7b- Index: Examples and Proofs
________________________________________________________
Page 5a- Dark-Dark-Light: Dark Matter = Dark Energy
Page 5b- The History of the Universe in Scalar Graphics
Page 5c- The History of the Universe_update: The Big Void
Page 6a- Geometry- Layout
Page 6b- Geometry- Space Or Time Area (SOTA)
Page 6c- Geometry- Space-Time Interactional Dimensions(STID)
Page 6d- Distillation of SI units into ST dimensions
Page 6e- Distillation of SI quantities into ST dimensions
Page 7- The LUFE Matrix Supplement: Examples and Proofs: Introduction-Layout & Rules
|Index|
| 7/I/A1 | 7/I/A2 | 7/I/A3 | 7/I/A4 | 7/I/A5 |
| 7/I/B1 | 7/I/B2 | 7/I/B3 | 7/I/B4 | 7/I/B5 |
| 7/I/C1 | 7/I/C2 | 7/I/C3 | 7/I/C4 | 7/I/C5 |
| 7/II/A1 | 7/II/A2 | 7/II/A3 | 7/II/A4 | 7/II/A5 |
| 7/II/B1 | 7/II/B2 | 7/II/B3 | 7/II/B4 | 7/II/B5 |
| 7/II/C1 | 7/II/C2 | 7/II/C3 |
| 7/II/D1 | 7/II/D2 | 7/II/D3 |
| 7/II/E1 | 7/II/E2 | |
| 7/III/A | 7/III/B | 7/III/C |
Page 7c- The LUFE Matrix Supplement: References
Page 8a- The LUFE Matrix: Infinite Dimensions
Page 9- The LUFE Matrix:E=mc2
Page 10- Quantum Gravity ...by the book
Page 11-Conservation of SpaceTime
Page 12-LUFE: The Layman's Unified Field Expose`
Copyright©2003-09 Reginald Brooks, BROOKS DESIGN. All Rights Reserved.
