| art theory 101~ Butterfly Prime Determinate Number Array (DNA) |
|---|
Butterfly Prime Determinate Number Array (DNA)
Copyright 2006, Reginald Brooks. All rights reserved.
Date completed: 02-15-06
Introduction
This work is based on the two original papers: "Butterfly Primes...~let the beauty seep in~" (2005), the author's original introduction to the wonderful, butterfly-like pattern of n24s shepherding the prime squares; and, "The Prime Number Directive...~metamorphosis~" (2006), providing further insight into the foundation of the "Butterfly Primes" pattern and the role of the odd non-prime numbers in establishing the primes.
A thorough read of the original two papers is a prerequisite to this work.
In "Butterfly Primes", three postulates and a new Prime Number Theorem were offered to summarize and codify the "Butterfly Primes" pattern. Taken together they define a beautiful ordered pattern within the primes. These postulates were based on a simple multiplication matrix (table).
Postulate 1 essentially defines the primes...and does so by elimination of all the other numbers, which are composites...composed of components other than or in addition to one and themselves.
Postulate 2 revealed the role of multiples of 24 (as n24) as the defining difference in the squares of any and all primes...including the next or any future primes.
Postulate 3, a restatement and refinement of Postulate 2 in visual...as well as mathematical... terms, presented the "Butterfly Primes" pattern as a modular, repeating, fractal-like pattern which both defines and predicts all prime number candidates.
The new Prime Number Theorem proposed: "A prime number is any natural whole number, greater than one, which is reducible only by itself and one, and, is always separated from the squares of all other primes (except P2,3,5) by multiples of 24. The infinity of primes can not exceed the infinity of n24".
"The Butterfly Prime Directive" took a harder look at all the odd numbers as seen through the filter of the n24 lens. The conclusion drawn was that all odd numbers fall into one of three groups:
Plan
In this paper, a further refinement presents the same information in a new clarifying light. Once again looking at the distinct patterns of the non-primes reveals the primes, and their pattern that emerges, to be that which is left over...a determinate number array. It is like finding a positive space pattern in the odd non-primes, only to reveal in the ensuing negative space so formed...the primes. The challenge is to present the patterns of both the positive and negative space...for one cannot see the one without the other...in clear and precise form!
Results
First, a little spotlight on the even numbers and their role in the "Butterfly Primes" pattern and then onto the Determinate Number Array form.
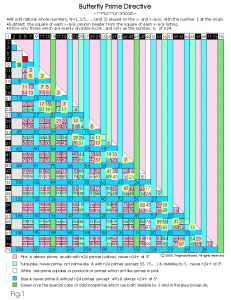
To note was that the predominant Blue Group, consisting of every third odd number (starting with 9), is a fixed, regular, non-variable pattern. Between each Blue Group odd number, there are two other odds which are variable...they may be either prime or "prime-like" (but non-prime)...and are referred to a prime number candidates (PNC). Fig. 1.
Fig. 1
(click to enlarge image)
Best viewed 800x600, F-11 key
(click here for Expanded Matrix image-(299 KB)
When the "Butterfly Primes" pattern was overlayed with the odd non-prime Blue Group (Fig. 2), it became visually clear that the n24s shepherding the primes in the "wings" of the butterfly are themselves shepherded by the Blue Group.
Fig. 2
(click to enlarge image)
Best viewed 800x600, F-11 key
Just as deepening the analysis of the role of n24 to the squares of not just the primes, but to all odd numbers, has revealed the larger patter shown in "The Butterfly Prime Directive", here, now, in "The Butterfly Prime Determinate Number Array", so too, has looking at some of the other n24 factors...(n3,n6), (n4,n8), (n2, n12, n24).
(n3), n6:
The two odd numbers sandwiched between the Blue Group odds are themselves separated...naturally... by an even number...and that even number is always a multiple of 6 (n6). Fig. 3 shows Fig.2 redrawn with the n6 evens group in Orange-Red and the primes in Black. It is interesting that n6 falls exactly midway between each Blue Group odd and this simultaneously places it exactly midway between each prime and/or "prime-like" candidate. In other words, next to every n6 entry there lies either a prime or a "prime-like" number. That the n6s are simply the Blue Group odds +/- 3 makes them no less fascinating. They are also the only even numbers divisible by 3 ( The Blue Group being the only odd numbers divisible by 3). See Table I.
Any odd number picked at random is a prime number candidate (PNC) if, and only if, it satisfies (n6=+/- 1).
(n4), n8:
The difference between any squared odd numbers is n8, increasing as n=(1),2,3,4,5,...
The difference between any squared Blue Group odd numbers - squared PNC is n8, increasing as n=(1),2,3,4,5,...
The difference between any squared PNC - squared Blue Group odd numbers is n8, increasing as n=(1),2,3,4,5,...
The difference between successive squared even numbers is n4, increasing as n=3,4,7,9,11...
(n2,n12), n24:
The difference between any squared Blue Group odd numbers is n24, increasing between each Blue Group as n=(3),6,9,12,15,...
The difference between any squared PNC odd numbers is n24, increasing by sets of 2, between each Blue Group, as n=(1),2,3,4,5,...
n8 & n24:
If the difference between any squared odd numbers is both n8 and n24, the smaller number is:
a PNC if the larger squared odd number is a PNC
or
a Blue Group member if the larger squared odd number is a Blue Group member.
See Table II.
Postulate 4: "Odds with n24, Evens with n6"
Within the sequence of the natural whole numbers (starting with 6), there exists a repetitive odd number slot...located immediately before and after all numbers that are divisible by 3...that is occupied by an odd number that is either prime or "prime-like" (but not prime), and is referred to as a prime number candidate (PNC).
Fig. 3
(click to enlarge image)
Best viewed 800x600, F-11 key
Table I
Table I. The Odd Numbers-BLUE Group & The Even n6 Numbers
All odd Every Only BLUE is evenly Only Orange-Red
numbers, Third # divided by 3, re- n6 evens are evenly
1-153... is BLUE generating the odds divided by 3, giving:
_______ _______ ___________________ ____________________
1 unit
3'
5'
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~6/3 = 2
7'
9~~~ BLUE /3 = 3
11'
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~12/3 = 4
13'
15~~~ BLUE /3 = 5
17'
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~18/3 = 6
19'
21~~~ BLUE /3 = 7
23'
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~24/3 = 8
25
27~~~ BLUE /3 = 9
29'
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~30/3 =10
...and so on |
Table II
Table II. The Role of n8 & n24 Separating Out the Blue Group from the PNC.
n8/n24 Row Group n24
_________________________________
| |
| 3 ******BLUE GROUP************ |
----------|_________________________________|__
| | |_________________
| | 5 ///// PNC //////////////// | | | | |
n24 -----------------------------------| n24 | | |
| | 7 ///// PNC //////////////// |_____| | | |
| _|__________________________________| n24 | |
----------| | | n24 |
| 9 ******BLUE GROUP************ | | | |
----------|_________________________________|__ | | n24
| | |_________| | |
| | 11 ///// PNC //////////////// | | | |
n24 -----------------------------------| n24 | |
| | 13 ///// PNC //////////////// |_____|_______| |
| _|__________________________________| |
----------| | |
| 15 ******BLUE GROUP************ | |
----------|_________________________________|__ |
| | | |_________________|
| n8-----| 17 ///// PNC //////////////// | |
n8 -----------------------------------| n24
|___________| 19 ///// PNC //////////////// |_____|
_|__________________________________|
| |
| 21 ******BLUE GROUP************ |
|_________________________________|__
_________ | |_____
| | 23 ///// PNC /////////////// | |
n8 -----------------------------------| n24
| n8-----| 25 ///// PNC /////////////// |_____|
| | _|__________________________________|
----------| |
| 27 ******BLUE GROUP************ |
|_________________________________|
|
Commentary
Looking along the axis of any of the Multiplication Matrix "Butterfly Primes" figures, one can see that every third number (starting with 6) is alternatively either an odd non-prime Blue Group member or an even non-prime Orange-Red Group member...and each is divisible by 3 and are the only such numbers. (Note: It is convenient to refer to this Orange-Red Group as based on n6 but do keep in mind that they are reducible to n3.)
The Blue Group has been discussed at length in "The Prime Number Directive" paper, and, of course, is based on filtering the odd numbers through the n24 lens. As the predominant odd number pattern, it immediately eliminates one-third of all the possible odd number prime candidates.
Since there are no even primes (above 2), the value of the n6 Orange-Red Group evens is that they provide yet another easy and specific marker for locating any and all prime or "prime-like" number candidates. When highlighted within the "Butterfly Primes" pattern, they generate yet another "mini" Butterfly pattern within each of the "wings" of the butterfly. Visual thinkers will readily appreciate this wonderful pattern within a pattern within a pattern form. See Fig. 4.
Fig. 4
(click to enlarge image)
Best viewed 800x600, F-11 key
(click here for Expanded Matrix image-(186 KB)
Postulate 5: "Primes vs Prime-like...Determinant Number Array"
The prime number candidates (PNC) consist of either primes or "prime-like", non-prime odd numbers...the difference being, by definition, that only the primes are irreducible (other than by one or themselves). From the pool of PNC, elimination of all numbers that are divisible by 5, and/or by another prime, leaves only the primes. A highly ordered and predictable pattern of odd non-prime, "prime-like" number candidates reveals the remaining primes as the reverse pattern...the negative space of the odd non-primes positive space...and therefore forming a determinant number array. Fig.5.
Fig. 5
(click to enlarge image)
Best viewed 800x600, F-11 key
(click here for Expanded Matrix image-(204 KB)
Commentary and Conclusion from "The Butterfly Prime Directive"
From "The Butterfly Prime Directive":"The multitude of numerical relationships, of which only a few have been elucidated here, is striking. That dividing the differences in the squares of the odd numbers by 24 should result in such an inter-related matrix grid with a resounding pattern separating out the prime and "prime-like" numbers from the relentless downbeat of the odd non-prime numbers gives one pause.
"Heretofore, it seem that the prime numbers...being prime...were the fundamental numbers...the chosen ones. The other numbers being simply derived from these prime sources. It is hard to argue against the formidable relationships that all numbers have as being distilled back to their prime number origins. This is even more true as we have seen in the new visual pattern of the primes squared being shepherded by n24s within the n24 "Butterfly Primes" pattern.
"Now it seems, with this further distillation of the odd numbers, their squares and the resulting relationships revealed when analyzed through the mathematical lens of n24, that it may have been premature to relegate such total primacy to those mysterious primes.
"A new force to reckon with is the power of the odd non-primes. At the very least, this bold and unyielding display of rhythmic numeric architecture holds its own against the sought after primes. And the dramatic contribution of a simple repetitive and enriching numerical scaffolding provides that very framework which allows for the presence of the meandering primes...and gives those primes a reason for existence and even the exalted status.
"The emphasis on simplicity and beauty which seems to inform so much of Nature's design would fully support this approach as primary: Build a reliable, reproducible and fully expandable framework of simple numbers starting with 1,2,3 (and 5). One is unitary. Two is its double and three generates structure (five is the penultimate). Every third odd number (starting with 9) will be the anchors of this framework (Blue). They are all non-primes and multiples of three, 3. Between these ribs shall be those remaining odd numbers...some of which are prime (Pink, and not divisible by 3, or 5, or any other number other than themselves and one), and, some which are "prime-like" (Turquoise and White, that are either divisible by 5 or are the products of primes). Together they form the rhythmic pattern of 1!-2-3, 1!-2-3, 1!-2-3,....
"It comes down to this. If you have an odd number it will be a member of one of three main groups:
"To note is that the pattern of distribution places the Blue Group as foremost in that it is fixed and unyielding...as every third odd number shall be Blue. Between, the two spaces remaining, may be filled in various combinations of Turquoise, White and Pink. [These are the PNC.]
"It may be especially noted that once the Blue (and Green), Turquoise and White groups are all filled by their non-prime (and some non-prime, but "prime-like") members, what remains...by default...are the Pinks...the prime numbers. The prime numbers are prime...meandering, mysterious and marvelous...because they are the numbers left over when all the regularity of numbers is taken out and sorted into separate non-prime groups. Even more amazing, is that these leftovers...these lovely primes...would be specifically courted, chaperoned and shepherded by select n24s within the "Butterfly Primes" pattern. The order...the seeming randomness...the order. The Butterfly Prime Directive. The beat goes on".
Proof and Clarification of the Determinant Number Array (Fig.5.)
The task at hand is show the highly ordered and predictable positive space pattern that the odd non-primes...both the redundant Blue Group members and the seemingly more sporadic Turquoise and White Group non-prime, "prime-like" candidates...make. The numbers which remain, and the negative space pattern that they form as determinant number array, are simply the primes. In some cases, this filtering will appear to be nothing more than the famous Sieve of Eratosthenes (ca 240 BC) or simple trial division, but what these and other tests of primality...from classical to neo-classical to modern... do not account for is the positive space pattern of the odd number divisors, whether they be prime or not. It is this pattern which reveals the reverse negative space pattern of the primes.
On the x- and y-axis layout all the odd numbers with one at the origin (two included as reminder). The x-axis will be the divisor, the y-axis the dividend, and within the matrix the numbers shown will not be the actual quotients, but simply that divisor that positively divided into that quotient at that spot on the grid.
The "3" column divisor along the x-axis thus divides into the 3,9,15,21,27,... dividends of the y-axis and a "3" is placed in each respective row in that column. These are, of course, members of the Blue Group...the smallest divisor of any member of this group is 3...so the entire row of each is colored blue.
The "5" column divisor divides into 5,15,25,35,45,...dividends on the y-axis, a "5" is placed in each respective row in that column. Those rows in which 5 is the smallest divisor are members of the Turquoise Group. Notice that row 15 has both 3 and 5 divisors. It remains a Blue Group as 3 is the smallest divisor. In fact, notice that every number has a natural appearance in the upper right diagonal as this simply represents every number divided by itself.
The "7" column divisor divides into 7,21,35,49,63,...dividends on the y-axis, a "7" is placed in each respective row in that column. Those rows in which 7 is the smallest divisor are members of the White Group. As before, resonances of lower divisors in other rows always keeps the color of the lowest divisor. To remain consistent with the "The Butterfly Prime Directive", all subsequent odd numbers that are not divisible by 3, 5 or their resonances (multiples) are members of the White Group. This works out as they are all products of primes anyway.
Together, the Turquoise and White Groups are part of the non-prime, "prime-like" group of numbers described in the earlier paper. Point of clarification: The use of the term "prime number candidate", or PNC, with or without the presence of the term "prime-like", simply refers to either a slot on the "Butterfly Primes" pattern, or, a particular class of results in the mathematical equations in the postulates, that points to a number place holder that if prime will always be here, but if not, will be occupied by one of the "prime-like", but not prime numbers, i.e. members of the Turquoise or White Groups. Blue Group members are never part of this as their number placement always places them before or after any of these "prime number candidate" slots (see Fig 2., 3.). Now for the patterns.
Vertical Columns:
The divisor "3" appears on every 3rd row number starting with 3.
The divisor "5" appears on every 5th row number starting with 5.
The divisor "7" appears on every 7th row number starting with 7.
The divisor "9" appears on every 9th row number starting with 9 and because it is a multiple of 3, it never appears on any row as the lowest divisor of that row, effectively neutralized as a row starter. The same goes for all resonances.
The divisor "11" appears on every 11th row number starting with 11. And so on.
The first time a divisor, that is not a resonance of another number, appears by itself as a row starter (lowest divisor) is when that number is squared, 32,52,72,112,132,...
The vertical spacing between subsequent adjacent divisors in each column increases by two just as the numbers do.
Diagonals:
Each diagonal repeats the Odd Number Sequence (ONS) as, 3,5,7,9,11,... See Fig. 3.
The first diagonal at the top is simply each x-axis dividend divided by itself...the y-axis divisor.
The second diagonal, beginning at 32 on the grid at row 9 is space at every 3rd row number, as 9,15,21,27,33,... and generates the ONS, 32,5,7,9,11,..., respectively.
The third diagonal, beginning at 52 (but extended up through 3) on the grid at row 15, is spaced at every 5th row number, as 15,25,35,45,55,... and generates the ONS as 3,52,7,9,11,...,respectively.
The fourth diagonal, beginning at 72 (but again extended up through 3) on the grid at row 21, is spaced at every 7th row number, as 21,35,49,63,77,... and generates the ONS as 3,5,72,9,11,...,respectively.
The fifth diagonal, beginning at 92 (but again extended up through 3) on the grid at row 27, is spaced at every 9th row number, as 27,45,63,81,99,... and generates the ONS as 3,5,7,92,11,..., respectively.
And so on with the same sequential pattern.
Horizontal Rows:
A distinct, orderly, repetitive and utterly predictable pattern of divisors emerges. This, together with the vertical and diagonal patterns becomes the positive form pattern of the odd non-prime numbers.
A harmonic wave analysis of this pattern can easily locate the common crossing nodes of each interval set of divisors with that of the subsequent sequential sets.
The 3 and 5 node repeats at rows 15,45,75,105,135,... at intervals of 30 whole numbers.
The 3 and 7 node repeats at rows 21,63,105,147,... at intervals of 42 whole numbers.
The 3 and 9 node repeats at rows 27,45,63,81,99,...at intervals of 18 whole numbers.
The 3 and 11 node repeats at rows 33,99,165,...at intervals of 66 whole numbers.
The 3,5,9, and 15 node repeats at rows 45,135,225,...at intervals of 90 whole numbers.
The pattern continues and expands indefinitely. Where ever the numbers repeat on a common row there is a node.
The reverse, background negative space pattern that remains is that of the primes...a numbered array determined by the pattern of the positive space odd non-primes. Notice that there are no divisor numbers in this negative space pattern. The Pink/Black prime group is defined by what it is not.
Conclusion
History has shown that often when looking for the trees the forest is not seen, and conversely, when looking for the forest, who knew there were trees. The pattern of the primes, while under the glare of the mathematical lights, has been elusive...yet tantalizingly close at hand. No doubt the primes were given the status of the trees and the other numbers, the rest of the forest, was little more than brush and saplings.
A more visual, less linear, approach to looking at the primes resulted in the "Butterfly Primes" pattern emerging from the common multiplication matrix (table). The pattern was striking, repetitive and largely predictable as formed from multiplies of an even number, 24, and referred to as n24. While giving an undeniably visual and mathematical presentation to the pattern of the primes it still left the motivation of this pattern unanswered. The notion of what is the forest...really?...was nevertheless raised.
The investigation continued. What is the relationship of any and all of the odd numbers to this n24? "The Butterfly Prime Directive" revealed a forest...a true forest...of big and little trees of at least several species, some of which were prime, some were "prime-like" (but not actually prime) and some of which were not prime or "prime-like" in any way. And these were just the trees of odd numbers. What about the trees of even numbers? Gradually, a picture of the forest...the true forest...of numbers began to emerge. The most striking finding was that most of the forest indeed did demonstrate a very strong resonating pattern throughout...but most especially on those trees of odd numbers that are not prime and when these were accounted for (including the even numbered trees), what remained was the prime number trees.
It has been the goal of this paper to focus and sharpen that new vision...that the definite, determinate number array pattern of the primes is formed from and best seen as the reverse pattern of the non-primes. The metaphor was changed. Instead of trees amongst the forest, it has been changed to terminology more appropriate to the technical descriptions of optics, vision and pictorial space...that of positive and negative space. Each defines the other and is equally dependent on the other. By refocusing on all the numbers, a distinct, orderly, repetitive and utterly predictable pattern that becomes the positive form pattern of the odd non-prime numbers emerges...and the reverse, background negative space pattern that remains is that of the primes...a numbered array determined by the pattern of the positive space odd non-primes.
Appendum-Addendum
(added 02-27-06)Fig. 6
(click to enlarge image)
Best viewed 800x600, F-11 key
References
The three excellent website references below provide outstanding information, presentation and resources about primes.
1. Caldwell, Chris, The Prime Pages,
http://primes.utm.edu
First and last source to check out everything you ever wanted to know about primes-history, glossary, proofs, types, lists, resources and more. Well referenced and up to date.
2. du Sautoy, Marcus, The Music of the Primes,
http://www.musicoftheprimes.com
A beautiful site which educates you as you go along the melody of mathematical thought. Particularly insightful presentation of imaginary numbers and the musical landscape metaphor elucidating Riemann's pursuit of the great ordered pattern of the primes.
3. Watkins, Matthew R., Number Theory and Physics,
http://www.maths.ex.ac.uk/~mwatkins/zeta/physics.htm
Embedded in the bigger picture of number theory and its relationship to physics, this wonderful site both teaches and inspires by relating the history of numerical and physical thought by their authors to a contemporary presentation of those ideas. Full of resources and great quotes.
Additional writings on art, math and physics by the author can be found at:
4. Brooks, Reginald, Art Theory 101,
http://www.brooksdesign-ps.net/Code/Html/arthry5.com
Additional and valuable links added post-publication:
5. Alfeld, Peter, http://www.math.utah.edu/~alfeld/
6. Chamness, Mark, http://alumnus.caltech.edu/~chamness/Prime.html
7. Edgington, Will, http://www.garlic.com/~wedgingt/mersenne.html
8. Heinz, Harvey, http://www.geocities.com/~harveyh/primes.htm
9. Leatherland, Adrian J.F., http://yoyo.cc.monash.edu.au/~bunyip/primes/
10. The Mathematical Association of America, http://www.maa.org
11. O'Connor, John and Edmund Robertson, http://www-history.mcs.st-and.ac.uk/history/HistTopics/Prime_numbers.html
12. Peterson, Ivars, http://www.sciencenews.org
13. Woltman, George, http://www.mersenne.org/prime.htm (GIMPS)
_________________________________________________________________________________________Copyright 2006, Reginald Brooks. All rights reserved.
Use
This paper and all its contents
© 2006, Reginald Brooks. All rights reserved. This work and all its content are, to the best knowledge of its author, original and solely of and by the author at the time of its creation. Permission is hereby granted for single copies to be made for personal, non-commercial use for students and teachers of schools, colleges and universities provided that: either the entire paper, including figures and tables, is kept intact; or, any extracts of the text, or figures or tables (in part or whole), be properly and visibly cited as to authorship and source.
Go to Butterfly Primes
(white paper), or
The Butterfly Prime Directive
(white paper), or
Butterfly Primes ~Prejudicial Numbers~ (new media net.art)