art theory 101~ Butterfly Prime Directive

Butterfly Prime Directive
~metamorphosis~

Copyright 2006, Reginald Brooks. All rights reserved.

Date completed: 01-05-06

 

Introduction

This work is based on the "Butterfly Primes...~let the beauty seep in~" (2005), the author's original introduction to the wonderful, butterfly-like pattern of n24s shepherding the prime squares. Three postulates outlined the now formidable characteristics, behavior, predictability and confirmation of all prime numbers.

The conjectures, which naturally follows, is that Riemann's Hypothesis, which ultimately is about proving an ordered pattern for the primes, has been resolved with this work. A new Prime Number Theorem was offered: "A prime number is any natural whole number, greater than one, which is reducible only by itself and one, and, is always separated from the squares of all other primes (except P2,3,5) by multiples of 24. The infinity of primes can not exceed the infinity of n24".

A thorough read of the original paper is a prerequisite to this work.

This paper, "The Prime Number Directive...~metamorphosis~", provides further insight into the foundation of the "Butterfly Primes" pattern and in doing so further substantiates the proof of Riemann's Hypothesis.

Plan

The investigation started with: If you were to take all the odd natural whole numbers, N=1,3,5,... (and the number 2) and place them on the x- and y-axis, with the number 1 at the origin, and subtract the square of each x-axis column header entry from the square of each y-axis entry, and show only those results which are evenly divisible by 24...and show those results only as the number, n, of n24s that were divisible...what would you find?

Results

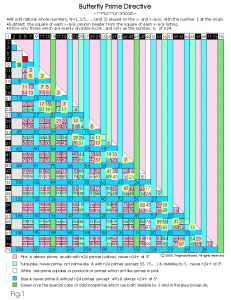
Fig.1, "The Butterfly Prime Directive...~metamorphosis~" was so compelling as it unfolded that the title was naturally born.

As laid out above, the squares of the odd horizontal, x-axis numbers were subtracted from those of the vertical, y-axis. After dividing the difference by 24, those which evenly divided as a whole number, n, were plotted on the matrix grid...and those that were prime were outlined in yellow.

A complete, inter-related maze of amazing patterns emerged. A great deal of the marvel of these patterns is no more than the consequence of applying a pattern of mathematical operations to the odd numbers. That the basis, the directive, of the underlying prime number and "Butterfly Primes" issues forth in such a metered, rhythmic pattern is most gratifying and fully substantiating the original work. Fig 2. presents an overlay of this new work directly over the "Butterfly Primes" figure from the original work (where is was Fig 3a). Seeing this now will help the reader digest the new work that now follows.

 

 

Fig 1:Butterfly Prime Directive ~Metamorphosis~

Fig. 1
(click to enlarge image)
Best viewed 800x600, F-11 key
(click here for Expanded Matrix image-(299 KB)

 

 

Fig 2:Butterfly Prime Directive ~Overlay~

Fig. 2
(click to enlarge image)
Best viewed 800x600, F-11 key

Axis

The x- and y-axis are identical layouts in which the primes are shown on a black background.

Matrix Grid

 ~COLORED BARS
    Primes
  • Pink are always prime, usually have n24 primes (yellow outline), and never have n24 results at the 32 position (from the horizontal x-axis at the far left).
    Non-Primes, but "Prime-like"
  • Turquoise (Green-Blue/Blue-Green), while never prime, act "prime-like". They are a group of odd non-primes which are divisible by 5, usually have n24 primes and never have n24 results at the 32 position. They are not in the Blue Group (see below)...and act like they are in the Pink prime group. Exceptions to this group (15,45,75,105,...) are in the Green Group below and it will be obvious why .
  • White are either prime squares (72, 112, etc.) or are the products of primes (7x11, 7x13, 7x17, 7x19, 11x13,...etc.) and act like primes in Pink.
    Non-Primes
  • Blue are never prime and always positive for n24 at the 32 position...and typically without n24 primes. In some respects, the Blue Group represents every odd number leftover which is not prime or "prime-like." In fact, Blue completely dominates the pattern (emphasized in the horizontal of Fig. 1) in a strict 1!-2-3, 1!-2-3, 1!-2-3 metered rhythm. Any colored bar group or base odd number which falls on the Blue's natural downbeat at 1, becomes a member of the Blue Group. Beats 2 and 3 remain for the prime and "prime-like" numbers. Blue is true. Every third odd number, starting with 9, falls into the Blue Group on this matrix grid and represents the non-prime squares between the n24 "Butterfly" highlights. Fig. 2. Table I.

    • Eventually, a Blue group odd number will fall within one of the n24 shepherding pairs that escort the prime number candidates (see the original paper). That it remains true Blue and non-prime can be seen as it is positive for n24 at the 32 position (which no prime ever is), and, it violates Postulate 3 from "Butterfly Primes." excerpted here:

    Postulate 3: "Butterfly Primes"

    a. An overlap of all multiples of 24 (n24) on the Multiplication Matrix (Table) reveals a visual and mathematically logical pattern ("Butterfly"). The squared primes, five and up, are always positioned exactly between two symmetrically placed n24s along side the diagonal "squares" line...effectively selecting out all prime candidates such that, taking the square root of, all even numbers along one axis times the same numbers increased by 2 on the other axis (whose product must equal n24)...and adding one to that product, (Figs 3a, b and c, Table III-in the original paper) generates the candidates, as:

    P2candidate = [Neven x (N+2)] + 1      (11)

    Pcandidate = ([Neven x (N+2)] + 1)½    (12)

    b. Applying the principles of Postulates 1 and 2 above eliminates all the spurious entries leaving only the squared primes.

  • Green (v) are those special odd non-primes that would like to be in the Turquoise Group, seeing that they are divisible by 5, but as they overlap the Blue Group positions they are in fact absorbed fully into that group... becoming non-prime and always positive for n24 at the 32 position...and typically without n24 primes. They are inescapably Blue!

    • In Table II, the relentless pattern of the Blue Group is laid out as a of every third odd number starting with 9. The difference is of course 6. In between each Green Group lies two sequential members of the Turquoise Group (outside of the Blue Group, by definition). As the Green Group increases sequentially by 30...as 15, 45, 75... between are two Turquoise Group members...as 25, 35...55, 65...etc. And similar to the rhythmic pattern of the Blue Group, the Green Group overlaps the Blue downbeats at 1 while the Turquoise Group follow in a "prime-like" pattern at the 2nd and 3rd beats.



Table I

 
 
     Table I. The Odd Numbers and the BLUE Group

     All odd  	Every       Only BLUE is evenly  
     numbers, 	Third #     divided by 3, re-
     1-153... 	is BLUE     generating the odds
     _______  	_______     ___________________ 
      1 unit
      3'   
      5' 
      7'
      9~~~ 	BLUE 	/3  =   3
     11'
     13'
     15~~~ 	BLUE 	/3  =   5
     17' 
     19'
     21~~~ 	BLUE 	/3  =   7
     23'
     25
     27~~~ 	BLUE 	/3  =   9
     29'
     31'
     33~~~ 	BLUE 	/3  =  11
     35
     37'
     39~~~ 	BLUE 	/3  =  13
     41'
     43'
     45~~~ 	BLUE 	/3  =  15
     47'
     49
     51~~~ 	BLUE 	/3  =  17              
     53'
     55
     57~~~ 	BLUE 	/3  =  19
     59'  
     61'   
     63~~~ 	BLUE 	/3  =  21
     65
     67'
     69~~~ 	BLUE 	/3  =  23
     71'
     73'    
     75~~~ 	BLUE 	/3  =  25
     77
     79'
     81~~~ 	BLUE 	/3  =  27
     83'
     85
     87~~~ 	BLUE 	/3  =  29
     89'
     91
     93~~~ 	BLUE 	/3  =  31
     95
     97' 
     99~~~ 	BLUE 	/3  =  33
    101'
    103'
    105~~~ 	BLUE 	/3  =  35
    107'
    109'
    111~~~ 	BLUE 	/3  =  37
    113'
    115
    117~~~ 	BLUE 	/3  =  39
    119
    121
    123~~~ 	BLUE 	/3  =  41
    125
    127'
    129~~~ 	BLUE 	/3  =  43
    131'
    133
    135~~~ 	BLUE 	/3  =  45
    137'
    139'
    141~~~ 	BLUE 	/3  =  47
    143
    145
    147~~~ 	BLUE 	/3  =  49
    149'
    151'
    153~~~ 	BLUE 	/3  =  51
    ...and so on


Table II

 
 
     Table II. The BLUE Group numbers

     Every BLUE Number ending in 5 is a GREEN Number converted to BLUE.
     
     All BLUE numbers, 9-1683..., are evenly divisible by 3 and never prime. 	    
     ______________________________________________________________________
   
      9		219	429	639	849	1059	1269	1479
     15		225	435	645	855	1065	1275	1485
     21		231	441	651	861	1071	1281	1491
     27		237	447	657	867	1077	1287	1497
     33		243	453	663	873	1083	1293	1503
	
     39		249	459	669	879	1089	1299	1509
     45		255	465	675	885	1095	1305	1515
     51		261	471     681	891	1101	1311	1521
     57		267	477	687	897	1107	1317	1527
     63		273	483	693	903	1113	1323	1533
  
     69		279	489	699	909	1119	1329	1539
     75		285	495	705	915	1125	1335	1545
     81		291	501	711	921	1131	1341	1551
     87		297	507	717	927	1137	1347	1557
     93		303	513	723	933	1143	1353	1563
 
     99		309	519	729	939	1149	1359	1569
    105		315	525	735	945	1155	1365	1575
    111		321	531	741	951	1161	1371	1581
    117		327	537	747	957	1167	1377	1587
    123		333	543	753	963	1173	1383	1593

    129		339	549	759	969	1179	1389	1599
    135		345	555	765	975	1185	1395	1605
    141		351	561	771	981	1191	1401	1611
    147		357	567	777	987	1197	1407	1617
    153		363	573	783	993	1203	1413	1623

    159		369	579 	789	999	1209	1419	1629
    165		375	585	795	1005	1215	1425	1635
    171		381	591	801	1011	1221	1431	1641
    177		387	597	807	1017	1227	1437	1647
    183		393	603	813	1023	1233	1443	1653

    189		399	609	819	1029	1239	1449	1659
    195		405	615	825	1035	1245	1455	1665
    201		411	621	831	1041	1251	1461	1671
    207		417	627	837	1047	1257	1467	1677
    213		423	633	843	1053	1263	1473	1683
    							...and so on


~NUMBERS (Fig. 3.)

Notice that the numbers in the matrix grid fall into two basic patterns with sequential number sequences on the main diagonal:

1. Prime or "Prime-like" square sets of four (Pink, White, & Turquoise).

2. Non-Prime square grid outlines, with the numbers at the crossings (Blue and Green).

  • 1.Prime or "Prime-like"
    • Sums of the diagonals of any square set(s) are equal.
    • Horizontally (L->R), the numbers decrease by 1,2,3...etc respectively in each set and the decrease is marked by the single number on the diagonal above.
    • Vertically (T->B, L->R), the numbers increase by 2,3,4...etc in each horizontal set and the increase is marked by the single number on the diagonal to the right.

  • 2. Non-Prime
    • Sums of the diagonals of any square set(s) are equal.
    • Horizontally (L->R), the numbers decrease by 3,6,9...etc respectively in each set and the decrease is marked by the first number at the top of that vertical column in Blue or Green.
    • Vertically (T->B, L->R), the numbers increase by 9,12,15...etc in each horizontal set and the increase is marked by the last number on the respective horizontal Blue bar.

  • 3. Primes & Non-Primes together Naturally, it follows that the sums of the diagonals of any rectangular set(s) spanning over any group(s) will also be equal.

  • 4. Diagonals In line-parallel to the main diagonal Starting with the major, centerline diagonal and working down: 
    • Sequential sequence 1,2,3... increasing by  1.
      • 

    •    "           "    3,5,7...    "        "  2.
      • 

    •    "           "    3,4,5...    "        "  1. Blue increases by 3.
      • 

    •    "           "    6,10,14...  "        "  4.
      • 

    •    "           "    10,15,20... "        "  5.
      • 

    •    "           "    9,11,13...  "        "  2. Blue increases by 6.
      • 

    •    "           "    14,21,28... "        "  7.
      • 

    •    "           "    20,28,36... "        "  8.
      • 

    •    "           "    18,21,24... "        "  3. Blue increases by 9.
      • 

    •    "           "    25,35,45... "        " 10.
      • 

    •    "           "    33,44,55... "        " 11.
      • 

    •    "           "    30,34,38... "        "  4. Blue increases by 12.
  • and so on. Notice the sequence 1-12 and 1-4 on the right.

    • Taking the diagonal members of each set of 4 squares as these sets traverse diagonally down and parallel to the main diagonal, they sum up with same difference between each subsequent set, i.e. 4+5=9 (or 6+3), 7+8=15 (or 10+5), 10+11=21 (or 14+7), the difference being 6. Moving down and in from the main diagonal, the same pattern emerges for each subsequent set, only the difference increases as 6,12,18...for each inner set.


    In line-perpendicular to the main diagonal Starting perpendicular to the major, centerline diagonal and working down: 
    • Sequential sequence 1,3...   increasing by  2.
      • 

    • (single number 4)     
      • 

    • Sequential     "    3,6,9...    "        "  3.  
      • 

    • (single number 5)  
      • 

    • (single number 11) 
      • 

    • Sequential     "    2,6,10...   "        "  4. Blue increases by 12.
      • 

    • (single number 13)   
      • 

    • Sequential     "    7,21,...    "        " 14.
      • 

    •    "           "    5,10,15...  "        "  5. Blue increases by 15.
      • 

    •    "           "    8,24,...    "        " 16.
      • 

    •    "           "    17,34,...   "        " 17.
      • 

    •    "           "    3,9,15...   "        "  6. Blue increases by 18.
      • 

    •    "           "    19,38...    "        " 19.
      • 

    •    "           "    10,30,50... "        " 20.
      • 

    •    "           "    7,14,21...  "        "  7. Blue increases by 21.
      • 

    •    "           "    11,33,55... "        " 22.
      • 

    •    "           "    23,46,69... "        " 23.
      • 

    •    "           "    4,12,20...  "        "  8. Blue increases by 24.
  • and so on. Notice the sequence 12-24 and 2-8 on the right (starts slowly).

    • Taking the diagonal members of each set of 4 squares as these sets traverse diagonally down and perpendicular to the main diagonal, they sum up with same difference between each subsequent set, i.e. set 1: 5+10=15 (or 7+8), 20+25=45 (or 21+24) the difference being 30; set 2: 15+21=36 (or 17+19), 33+39=72 (or 34+38) the difference being 36; set 3: 7+14=21 (or 10+11), 28+35=63 (or 30+33), 49+56=105 (or 50+55) the difference being 42, and so on. Moving down and perpendicular to the main diagonal, the same pattern emerges for each subsequent set, the difference increases as 6,12,18...for each inner set as above...only the sequence begins at 30.


    • 5. More on the Blue Group
      • Adding the diagonal numbers (3,6,9,12,15,...) as a summation series generates the answers horizontally (9,18,30,45,63,...respectively)on the far left.
      • The sum of the first and last number on any Blue horizontal bar is found in the second position (L->R) on the Blue bar below.
      • The difference between any number and the last number on any Blue horizontal bar is found directly on the Blue bar above. (Same is true for the prime and "prime-like" sets.)
      • The sums of any Blue horizontal row are always evenly divisible by 3.
      • The sums of any Blue horizontal row, divided by its y-axis odd non-prime header number at the beginning of that row, generates a quotient which is an exact interval of 0.33331/3 and is expressed as either a whole number or as a whole number plus 0.33331/3 as shown in Table III below. The number of 0.33331/3 intervals advances as 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, ... from the respective quotients of 0.33331/3, 1, 2, 3.33331/3, 5, 7, 9.33331/3, 12, 15, 18.33331/3, 22, 26, .... That interval increases from each previous number sequentially as 2,3,4,5,6,.... Also do note that taking the difference of the difference of the horizontal Blue row generates the same odd number series as dividing the y-axis Blue header number by 3, beginning with number 5 as shown in the table.

    • Fig 3:Butterfly Prime Directive ~A Simplification~

    Fig. 3
    (click to enlarge image)
    Best viewed 800x600, F-11 key

    Table III

     
     Table III. The Odd Numbers and the BLUE Group

     BLUE  	BLUE sum              # of      difference  BLUE y-axis
     y-axis,    divided by its        0.3331/3s  between #   divided by
     9-153... 	y-axis number                                    3
     _______  	________________      ________  _________   ___________
 
      9~~~ 	     3/9  =  0.3331/3     1	 		 3
     15~~~ 	   15/15  =  1  	  3 	   2		 5
     21~~~ 	   42/21  =  2 		  6	   3		 7
     27~~~ 	   90/27  =  3.3331/3  	 10 	   4		 9
     33~~~ 	  165/33  =  5 		 15	   5		11
     39~~~ 	  273/39  =  7 		 21	   6		13
     45~~~ 	  420/45  =  9.3331/3 	 28	   7		15
     51~~~ 	  612/51  = 12 		 36	   8		17              
     57~~~ 	  855/57  = 15 		 45	   9		19   
     63~~~ 	 1155/63  = 18.3331/3 	 55	  10		21
     69~~~ 	 1518/69  = 22 		 66	  11		23    
     75~~~ 	 1950/75  = 26 		 78	  12		25
     81~~~ 	 2457/81  = 30.3331/3 	 91	  13		27
     87~~~ 	 3045/87  = 35 		105	  14		29
     93~~~ 	 3720/93  = 40 		120	  15		31 
     99~~~ 	 4488/99  = 45.3331/3 	136	  16		33
    105~~~ 	 5355/105 = 51 		153	  17		35
    111~~~ 	 6327/111 = 57 		171	  18		37
    117~~~ 	 7410/117 = 63.3331/3 	190	  19		39
    123~~~ 	 8610/123 = 70 		210	  20		41
    129~~~ 	 9933/129 = 77 		231	  21		43
    135~~~ 	11385/135 = 84.3331/3 	253	  22		45
    141~~~ 	12972/141 = 92 		276	  23		47
    147~~~ 	14700/147 =100 		300	  24		49

    ...and so on


    Commentary and Conclusion

    The multitude of numerical relationships, of which only a few have been elucidated here, is striking. That dividing the differences in the squares of the odd numbers by 24 should result in such an inter-related matrix grid with a resounding pattern separating out the prime and "prime-like" numbers from the relentless downbeat of the odd non-prime numbers gives one pause.

    Heretofore, it seem that the prime numbers...being prime...were the fundamental numbers...the chosen ones. The other numbers being simply derived from these prime sources. It is hard to argue against the formidable relationships that all numbers have as being distilled back to their prime number origins. This is even more true as we have seen in the new visual pattern of the primes squared being shepherded by n24s within the n24 "Butterfly Primes" pattern.

    Now it seems, with this further distillation of the odd numbers, their squares and the resulting relationships revealed when analyzed through the mathematical lens of n24, that it may have been premature to relegate such total primacy to those mysterious primes.

    A new force to reckon with is the power of the odd non-primes. At the very least, this bold and unyielding display of rhythmic numeric architecture holds its own against the sought after primes. And the dramatic contribution of a simple repetitive and enriching numerical scaffolding provides that very framework which allows for the presence of the meandering primes...and gives those primes a reason for existence and even the exalted status.

    The emphasis on simplicity and beauty which seems to inform so much of Nature's design would fully support this approach as primary: Build a reliable, reproducible and fully expandable framework of simple numbers starting with 1,2,3 (and 5). One is unitary. Two is its double and three generates structure (five is the penultimate). Every third odd number (starting with 9) will be the anchors of this framework (Blue). They are all non-primes and multiples of three, 3. Between these ribs shall be those remaining odd numbers...some of which are prime (Pink, and not divisible by 3, or 5, or any other number other than themselves and one), and, some which are "prime-like" (Turquoise and White, that are either divisible by 5 or are the products of primes). Together they form the rhythmic pattern of 1!-2-3, 1!-2-3, 1!-2-3,....

    It comes down to this. If you have an odd number it will be a member of one of three main groups:

    • 1!-Blue (and Green) is the predominate group of non-primes;
    • 2-Turquoise/White, is one of the two subdominant non-prime, "prime-likes";
    • 3-Pink primes.

    To note is that the pattern of distribution places the Blue Group as foremost in that it is fixed and unyielding...as every third odd number shall be Blue. Between the two spaces remaining may be filled in various combinations of Turquoise, White and Pink.

    It may be especially noted that once the Blue (and Green), Turquoise and White groups are all filled by their non-prime (and some non-prime, but "prime-like") members, what remains...by default...are the Pinks...the prime numbers. The prime numbers are prime...meandering, mysterious and marvelous...because they are the numbers left over when all the regularity of numbers is taken out and sorted into separate non-prime groups. Even more amazing, is that these leftovers...these lovely primes...would be specifically courted, chaperoned and shepherded by select n24s within the "Butterfly Primes" pattern. The order...the seeming randomness...the order. The Butterfly Prime Directive. The beat goes on.

    References

    The three excellent website references below provide outstanding information, presentation and resources about primes.

    1. Caldwell, Chris, The Prime Pages,
    http://primes.utm.edu

    First and last source to check out everything you ever wanted to know about primes-history, glossary, proofs, types, lists, resources and more. Well referenced and up to date.

    2. du Sautoy, Marcus, The Music of the Primes,
    http://www.musicoftheprimes.com

    A beautiful site which educates you as you go along the melody of mathematical thought. Particularly insightful presentation of imaginary numbers and the musical landscape metaphor elucidating Riemann's pursuit of the great ordered pattern of the primes.

    3. Watkins, Matthew R., Number Theory and Physics,
    http://www.maths.ex.ac.uk/~mwatkins/zeta/physics.htm

    Embedded in the bigger picture of number theory and its relationship to physics, this wonderful site both teaches and inspires by relating the history of numerical and physical thought by their authors to a contemporary presentation of those ideas. Full of resources and great quotes.

    Additional writings on art, math and physics by the author can be found at:

    4. Brooks, Reginald, Art Theory 101,
    http://www.brooksdesign-cg.com/Code/Html/arthry2.com


    Additional and valuable links added post-publication:

    5. Alfeld, Peter, http://www.math.utah.edu/~alfeld/

    6. Chamness, Mark, http://alumnus.caltech.edu/~chamness/Prime.html

    7. Edgington, Will, http://www.garlic.com/~wedgingt/mersenne.html

    8. Heinz, Harvey, http://www.geocities.com/~harveyh/primes.htm

    9. Leatherland, Adrian J.F., http://yoyo.cc.monash.edu.au/~bunyip/primes/

    10. The Mathematical Association of America, http://www.maa.org

    11. O'Connor, John and Edmund Robertson, http://www-history.mcs.st-and.ac.uk/history/HistTopics/Prime_numbers.html

    12. Peterson, Ivars, http://www.sciencenews.org

    13. Woltman, George, http://www.mersenne.org/prime.htm (GIMPS)

    _________________________________________________________________________________________

    Copyright 2006, Reginald Brooks. All rights reserved.

    Use

    This paper and all its contents © 2006, Reginald Brooks. All rights reserved. This work and all its content are, to the best knowledge of its author, original and solely of and by the author at the time of its creation. Permission is hereby granted for single copies to be made for personal, non-commercial use for students and teachers of schools, colleges and universities provided that: either the entire paper, including figures and tables, is kept intact; or, any extracts of the text, or figures or tables (in part or whole), be properly and visibly cited as to authorship and source.

    Go to Butterfly Primes (white paper), or
    The Butterfly Prime Determinate Number Array (white paper), or
    Butterfly Primes ~Prejudicial Numbers~ (new media net.art)

    Copyright©2006-08 Reginald Brooks, BROOKS DESIGN. All Rights Reserved.
    net.art index | netart01: RealSurReal...aClone | netart02: funk'n DNA/Creation GoDNA | netart03: 9-11_remembered | netart04: Naughty Physics (a.k.a. The LUFE Matrix) | netart05: Your sFace or Mine? | netart06: Butterfly Primes | >netart07: Geometry of Music Color | net.games | Art Theory 101 / White Papers Index | GoDNA | SCoDNA | PIN-Pattern in Numbers | Butterfly Primes | Butterfly Prime Determinant Number Array | GoMAS: The Geometry of Music, Art and Structure