Simple Path from the BIM to the PRIMES

SUMMARY*

(~from "*Simple Path from the BIM to the PRIMES" that presents the algebraic-geometry method.)

How do we go from the simple grid of the BIM (BBS-ISL Matrix) to identifying the PRIMES?

1. The BIM is a symmetrical grid — divided equally down its diagonal center with the Prime Diagonal (PD) — that illuminates the Number Pattern Sequence (NPS) of the Inverse Square Law (ISL) via simple, natural Whole Integer Numbers (WIN).

2. The BIM Axis numbers are 1,2,3,.. with 0 at the origin.

3. The Inner Grid (IG) contains EVEN and ODD WIN, but except for the 1st diagonal next to the PD — a diagonal that contains ALL the ODD WIN — there are NO PRIMES (NO-PRIMES, NP) on the SIG (Strict Inner Grid).

4. The PD WIN are simple the square of the Axis WIN.

5. ALL the IG WIN result from subtracting the horizontal from the vertical intersection of the PD.

6. Dropping down a given PD Squared WIN (>4) until it intersects with another squared WIN on a Row below will ALWAYS reveal that Row to be a Primitive Pythagorean Triple (PPT) Row, whose hypotenuse, c, lies on the intersecting PD. ALL PPTs may be identified this way.

7. Dividing the BIM cell values by 24 — BIM÷24 — forms a criss-crossing DIAMOND NPS that divides the overall BIM into two distinct and alternating Row (and Column) bands or sets:

   • ODD WIN that are ÷3 and referred to as NON-ARs;
   • ODD WIN that are NOT ÷3 and referred to as ARs, or Active Rows;
   • The ARs ALWAYS come in pairs — with an EVEN WIN between — as the UPPER and LOWER AR of the ARS (Active Row Set);

8. ALL PPTs and ALL PRIMES ALWAYS are found exclusively on the ARs — no exceptions.

9. By applying:

         (1)                  * $6yx ± y = NP$

   let y = odd number (ODD) 3, 5, 7,… and x = 1, 2, 3,... one generates a NP table containing ALL the NP;

   *True if ÷3 ODDs are first eliminated, otherwise ADD exponentials of 3 to the NP pool;

10. Eliminating the NP — and the NP contain a NPS — from ALL the ODD WIN, reveals the PRIMES (P).

11. A necessary, but not sufficient confirmation — but not proof — of primality is found by finding the even division of 24 into the difference of the square of ANY two PRIMES as:

          (2)                  (P₂)² - (P₁)² = $n24$

    let $n = 1, 2, 3,...$

    Be aware that this also holds true for ALL the AR NP. The P and NP are NOT ÷3, and are both part of the ARS and therefore any combination of the two squared differences will be ÷24:

          (3)                  (NP₂)² - (NP₁)² = $n24$

          (4)                  (NP₂)² - (P₁)² = $n24$

          (5)                  (P₂)² - (NP₁)² = $n24$

    The ÷3 NON-AR set is separately ÷24, but can NOT be mixed with members of the AR set (ARS) as:

          (6)                  (NON-AR-NP₂)² - (NON-AR-NP₁)² = n24

          (7)                  (NON-AR-NP₂)² - (NP₁)² ⧣ $n24$

          (8)                  (NP₂)² - (NON-AR-NP₁)² ⧣ $n24$

          (9)                  (P₂)² - (NON-AR-NP₁)² ⧣ $n24$

          (10)                (NON-AR-NP₂)² - (P₁)² ⧣ $n24$

    The division into AR and NON-AR sets has a NPS that ultimately define the elusive pattern of the P.

    Furthermore, $6yx ± y = NP$ may be re-arranged to:

          (11)                  $(NP ± y)/6yx = 0$

          (12)                  $(NP ± y) /6x = y$

    asking whether any given ODD (>3) is a P or NP, it is exclusively a NP if, and only if, y reduces to the same value after applying x. As y is effectively an ODD of either a PRIME or composite of PRIMES factor*, one only needs to satisfy a single instance to validate NON-Primality.

12. One can also obtain ALL the P by eliminating the BIM SIGO and O² from the 1^st Diagonal WIN, where SIGO = Strict Inner Grid ODDs, O² = ODDs², and the 1^st Diagonal = the 1^st Diagonal Parallel to the PD.

    This itself is further simplified by switching out the ODD AXIS values with the O² — the O² being the PD values — such that we now have:

          (13)   SIGO(A²) = Strict Inner Grid ODDS & ODD AXIS² giving a distinct visualization advantage;

          (14)                  NP = SIGO(A²)

          (15)                  1st Diagonal - SIGO(A²) = P.

This second method — the algebraic geometry method — as presented here.

Introduction

Two methods — one pure algebraic and the other a more visual algebraic geometry presented here — have been found that capture ALL the NO-PRIMES (NP). While they process slightly different, they dovetail nicely into a very visual Number Pattern Sequence (NPS) here on the BIM. They both give identical NP results.

So what is the significance of capturing ALL the NP?

The NP are the highly NPS that define the elusive pattern of the P. P + NP = ALL ODD WINs (≥3).

In any group of WIN, if you know the NP, you also know the P. Here is the highly visualizable geometric method for capturing ALL NP. In fact, it is just as simply stated in 12. of the SUMMARY.

Algebraic Geometry Method

One can obtain ALL the P by eliminating the BIM SIGO and O² from the 1^st Diagonal WIN, where SIGO = Strict Inner Grid ODDs, O² = ODDs², and the 1^st Diagonal = the 1^st Diagonal Parallel to the PD.

This itself is further simplified by switching out the ODD AXIS values with the O² — the O² being the PD values — such that we now have:

One can also obtain ALL the P by eliminating the BIM SIGO and O² from the 1^st Diagonal WIN, where SIGO = Strict Inner Grid ODDs, O² = ODDs², and the 1^st Diagonal = the 1^st Diagonal Parallel to the PD.

This itself is further simplified by switching out the ODD AXIS values with the O² — the O² being the PD values — such that we now have:

      (13)   SIGO(A²) = Strict Inner Grid ODDS & ODD AXIS²

      (14)                  NP = SIGO(A²)

      (15)                  1st Diagonal - SIGO(A²) = P.

The PDFs will follow these animated gifs. Videos and other supporting graphics thereafter.

Animated Gifs:

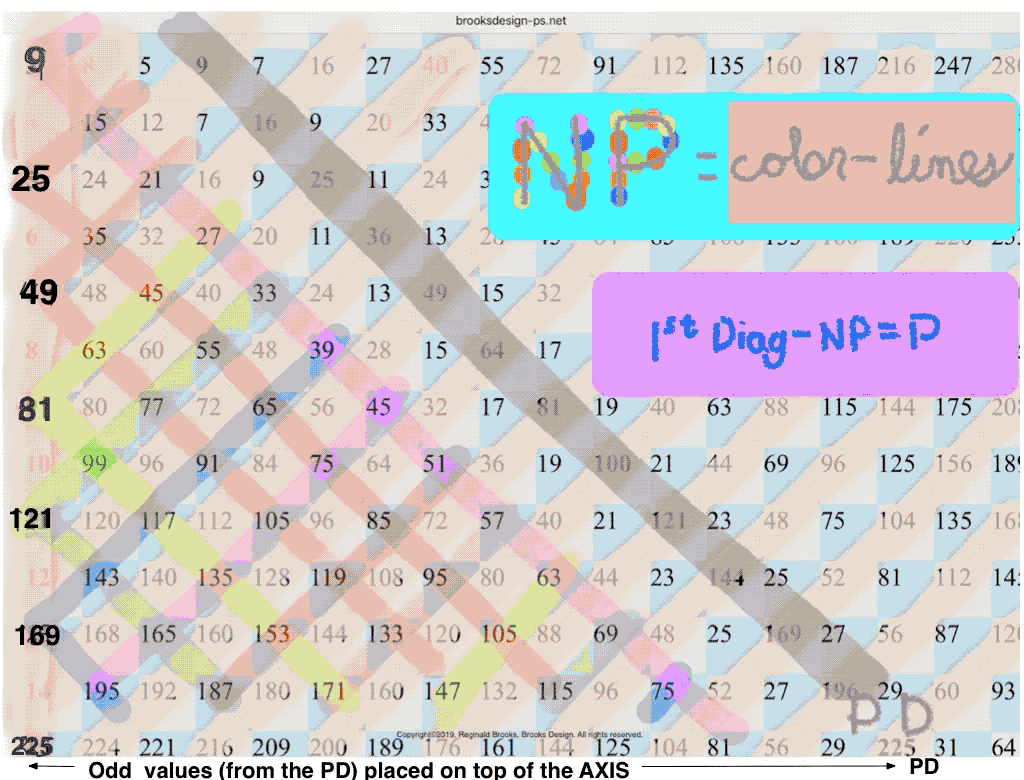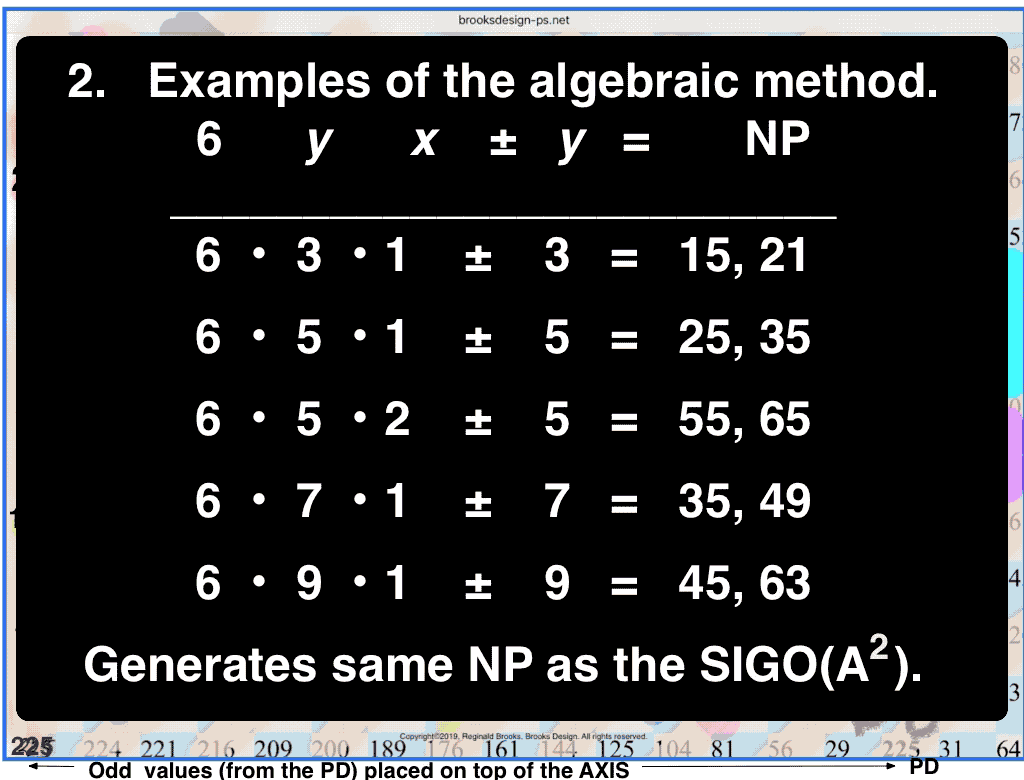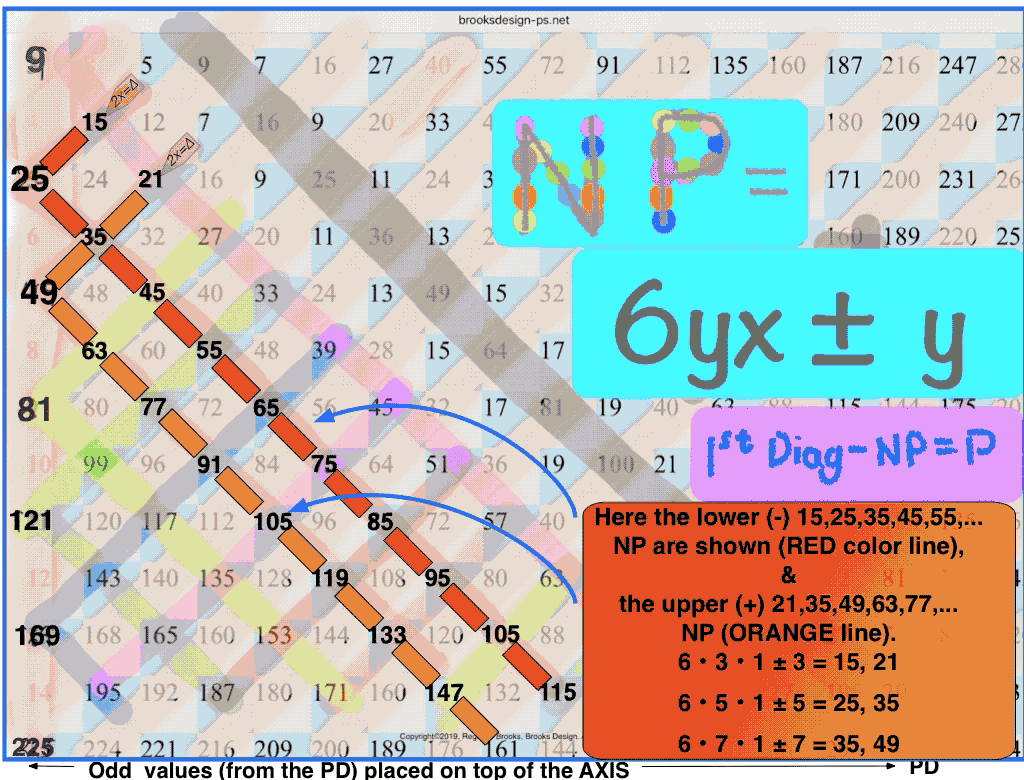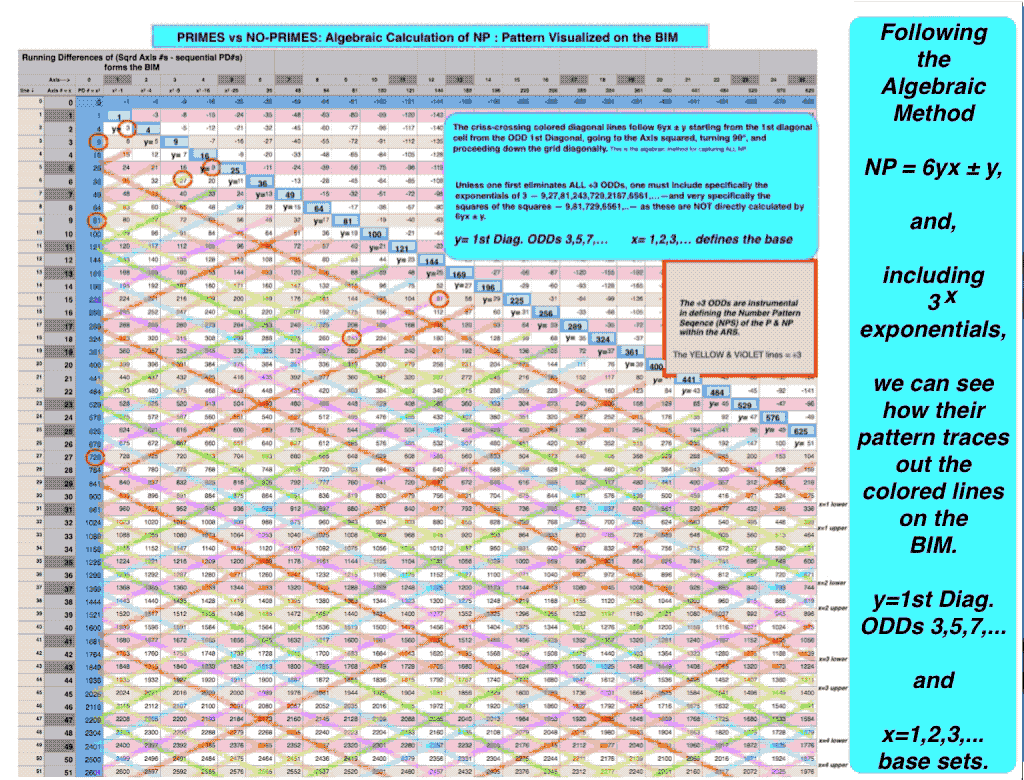
PRIMES vs NO-PRIMES-2: algebraic method.

PRIMES vs NO-PRIMES-1: algebraic-geometry method.

PRIMES vs NO-PRIMES-3: algebraic and algebraic geometry method.

PRIMES vs NO-PRIMES-4: algebraic method in detail.

PDFs +

PRIMES vs NO-PRIMES: snapshot-1 showing dovetailing visualization of the algebraic method of calculating the NP with that of the geometric method on the BIM. The larger PDF is below.

PRIMES vs NO-PRIMES PDF: snapshot-1 showing dovetailing visualization of the algebraic method of calculating the NP with that of the geometric method on the BIM. The NPS of the NP define the elusive pattern of the P.

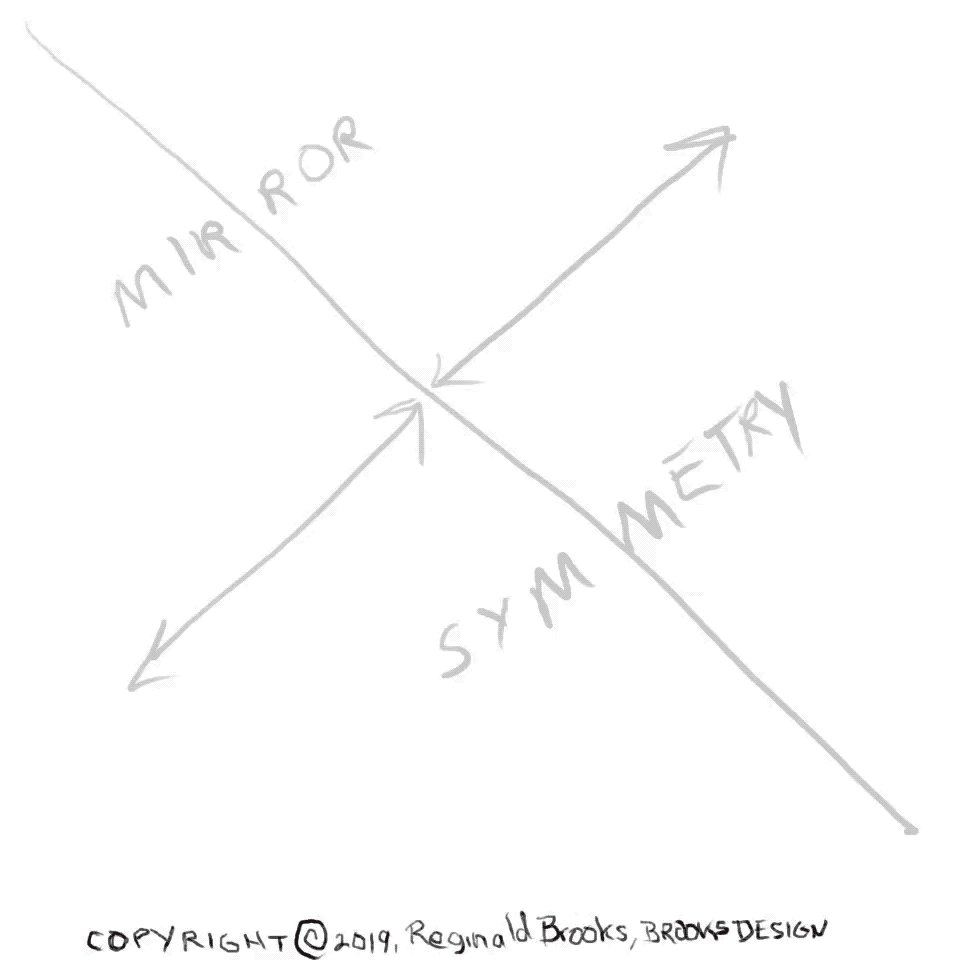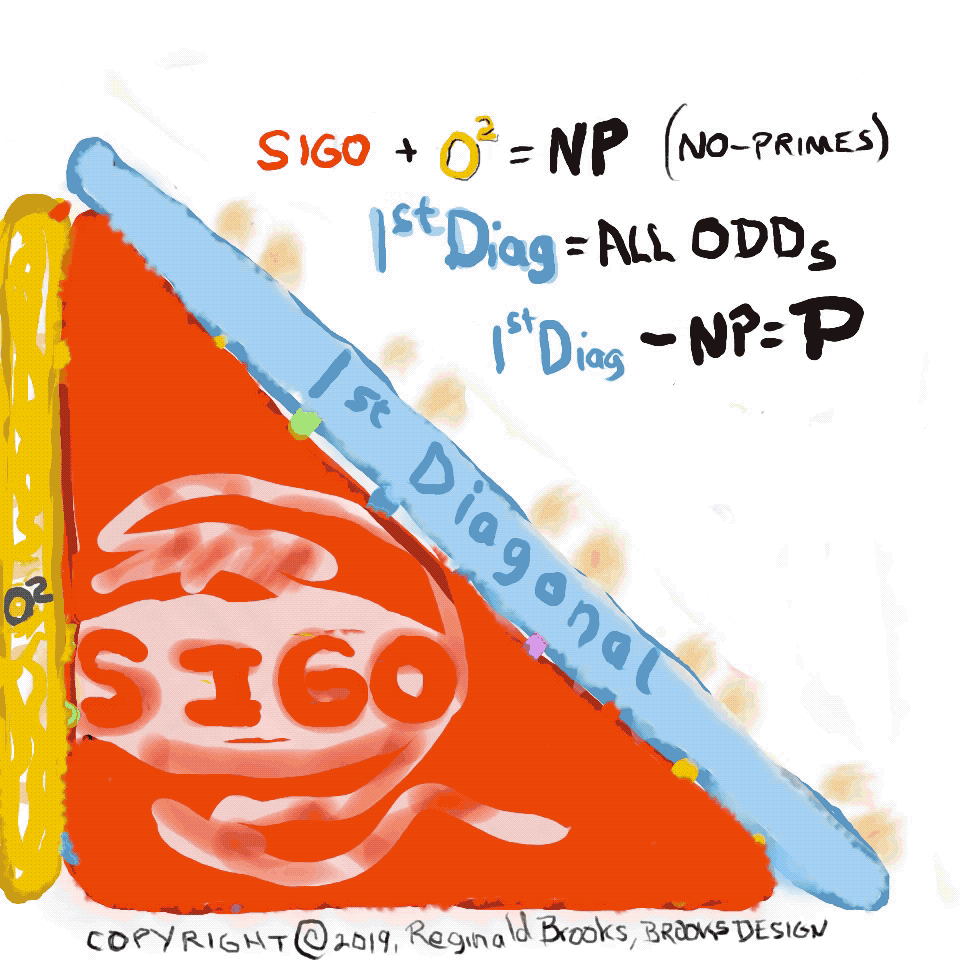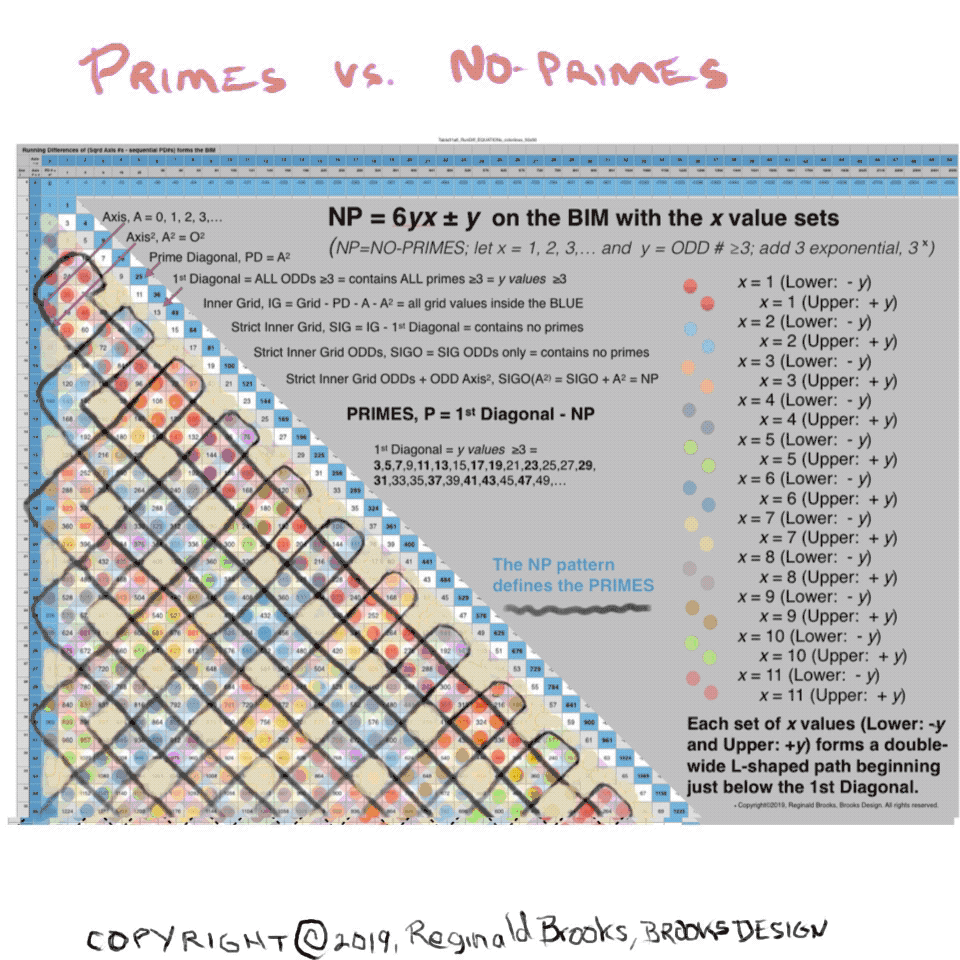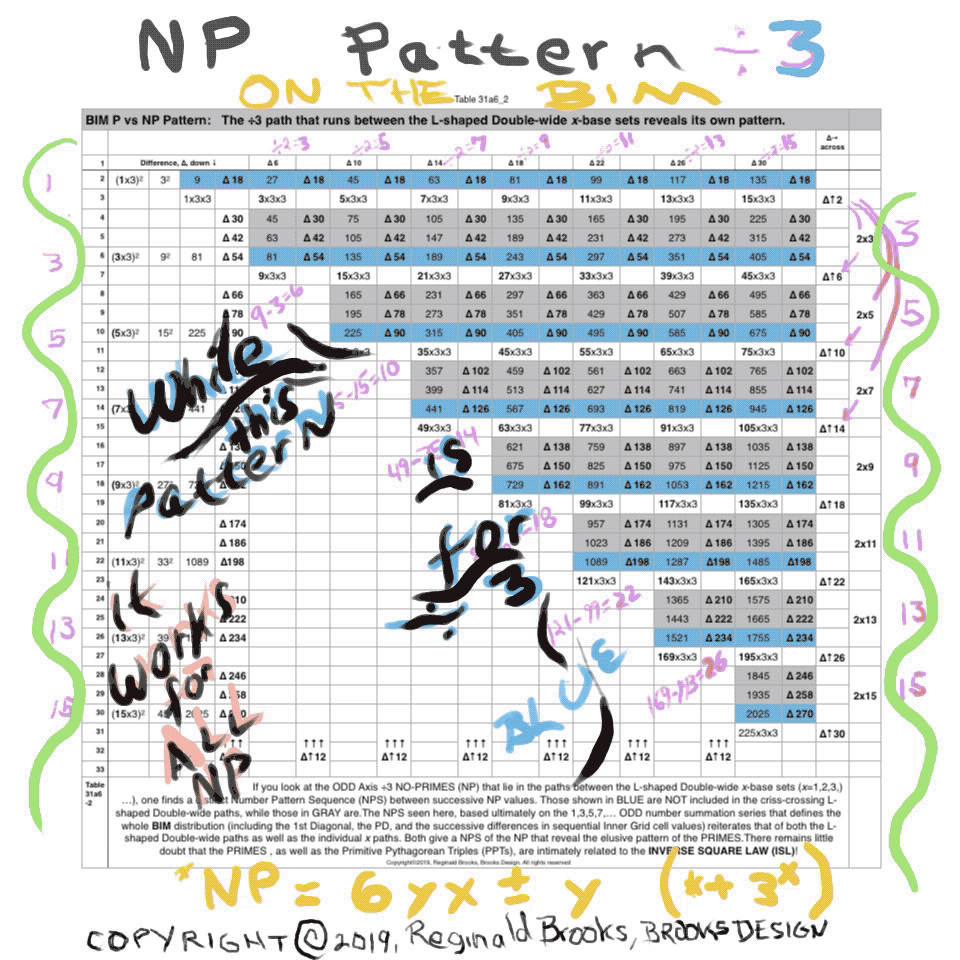
PRIMES vs NO-PRIMES: snapshot-2 showing dovetailing visualization of the algebraic method of calculating the NP with that of the geometric method on the BIM. Here the x=1,2,3,... base value sets -- Lower -y an Upper +y--as double-wide, L-shaped paths beginning just below the 1st Diagonal. These double rows alternate with divisible by 3--or divisible by 9 Axis squared--paths. The larger PDF is below.

PRIMES vs NO-PRIMES PDF: snapshot-2 showing dovetailing visualization of the algebraic method of calculating the NP with that of the geometric method on the BIM. The larger PDF is below. Here the x=1,2,3,... base value sets -- Lower -y an Upper +y--as double-wide, L-shaped paths beginning just below the 1st Diagonal. These double rows alternate with divisible by 3--or divisible by 9 Axis squared--paths.

PRIMES vs NO-PRIMES: snapshot-3 showing dovetailing visualization of the algebraic method of calculating the NP with that of the geometric method on the BIM. Here the x=1,2,3,... base value sets -- Lower -y an Upper +y--as double-wide, L-shaped paths beginning just below the 1st Diagonal. These double rows alternate with divisible by 3--or divisible by 9 Axis squared--paths. The larger PDF is below.

PRIMES vs NO-PRIMES PDF: snapshot-3 showing dovetailing visualization of the algebraic method of calculating the NP with that of the geometric method on the BIM. The larger PDF is below. Here the x=1,2,3,... base value sets -- Lower -y an Upper +y--as double-wide, L-shaped paths beginning just below the 1st Diagonal. These double rows alternate with divisible by 3--or divisible by 9 Axis squared--paths.

PRIMES vs NO-PRIMES PDF: snapshot-4 showing dovetailing visualization of the algebraic method of calculating the NP with that of the geometric method on the BIM. The larger PDF is below. Here the x=1,2,3,... base value sets -- Lower -y an Upper +y--as double-wide, L-shaped paths beginning just below the 1st Diagonal. These double rows alternate with divisible by 3--or divisible by 9 Axis squared--paths.

Table31a4: PRIMES vs NO-PRIMES PDF: Open in a separate tab/window to see all 11 pages. Here the x=1,2,3,... base value sets -- Lower -y an Upper +y--are shown individually and collectively as sets. The full Upper and Lower tables conclude.

Table31a6_2: PRIMES vs NO-PRIMES PDF: If you look at the ODD Axis ÷3 NO-PRIMES (NP) that lie in the paths between the L-shaped Double-wide x-base sets (x=1,2,3,)…), one finds a distinct Number Pattern Sequence (NPS) between successive NP values. Those shown in BLUE are NOT included in the criss-crossing L-shaped Double-wide paths (seen in the snapshots above), while those in GRAY are. The NPS seen here, based ultimately on the 1,3,5,7,… ODD number summation series that defines the whole BIM distribution (including the 1st Diagonal, the PD, and the successive differences in sequential Inner Grid cell values) reiterates that of both the L-shaped Double-wide paths as well as the individual x paths. Both give a NPS of the NP that reveal the elusive pattern of the PRIMES. There remains little doubt that the PRIMES , as well as the Primitive Pythagorean Triples (PPTs), are intimately related to the INVERSE SQUARE LAW (ISL)!

Videos:

PRIMES vs NO-PRIMES-1-long from Reginald Brooks on Vimeo.

PRIMES vs NO-PRIMES-2-long from Reginald Brooks on Vimeo.

PRIMES vs NO_PRIMES 3 from Reginald Brooks on Vimeo.

PRIMES_vs_NO-PRIMES-4 from Reginald Brooks on Vimeo.

...more supporting graphics and tables:

Table31a4-5_+RunDiff_EQUATIONsDEMO(÷3Filter)+10x10+. A simple table to demo the NP process.

Table31a4_+RunDiff_EQUATION-PATTERNS-LOWER+UPPER+Annotated. NP Table with layout notes.

Table31a4_+RunDiff_EQUATIONs(SqrdAxis-seqPD)+50x500+.pdf. From the BIM to the NP/P Tables.

                                          BIM35-Table31a4-5_NO-PRIMES_Factores-withARS-YELLOW-numbAnnotated. The NP pattern on the BIM.

Table33a,c,d_ODDsqrd÷24_sheets. The NP pattern – an amazing NPS – defines the P.

BIMrows1-1000+Primes_sheets+Sub-Matrix2. A BIM reference showing ÷24 ARS, PPTs, NP an P.

For the full documentation of all the graphics and pdfs — including history, development, expanded tables, and more — see the link references immediately below. Appendix B has all the documentation.

REFERENCES

While there are no specific references for this work other than referring back to my own original work, there are many references involved in the study and research on the PRIMES in general. These have been well documented in the TPISC_IV: Details_BIM+PPT+PRIMES focus white paper. This paper also contains the background graphics and tables leading up to this current work. The focus page is part of the much larger TPISC_IV: Details ebook project that is freely available as an HTML webpage. The quick reference outline can be found here.

BACK: ---> Part I of II CaCoST-DSEQEC on a separate White Paper

BACK: ---> Part II of II CaCoST-DSEQEC on a separate White Paper

BACK: ---> PRIMES vs NO-PRIMES on a separate White Paper

BACK: ---> TPISC_IV: Details_BIM+PTs+PRIMES on a separate White Paper

BACK: ---> PRIME GAPS on a separate White Paper

BACK: ---> PeriodicTableOfPrimes(PTOP)_GoldbachConjecture on a separate White Paper

BACK: ---> TPISC IV: Details White Paper

Artwork referencing TPISC.