PTOP: Periodic Table Of PRIMES: How to Make with Fractals

Introduction

What if the secret of the primes were to be more than just atomic-base units of the natural whole numbers.

What if they really gained their constructive prowess when their natural sequence — the PRIMES Sequence (PS = 3,5,7,11,13,17,19,23,29,31,...) — were tied together as PSs.

Yes as FRACTALS! PS-Fractals.

(Side Note: This is easy enough to do, especially if we disregard PRIME 2, as ALL the remaining PRIMES are ODD #s. PRIME 2, the ONLY EVEN PRIME, could be thought of as composed of PRIME 1 + PRIME 1, but since we now do not allow 1 to be PRIME, 2 being there is really quite silly — a techno-derived result. Lose the 1, lose the 2!)

The PS-Fractals are characterized as:

1. The strictly follow the PS;
2. The spacing — PRIME Gaps — between the PS is strictly followed;
3. When combined with another PRIME in sets — P₁, P₂ — to form PPsets, only 1 member of the set is variable, the other remains constant, as the sets form groupings, strings or “TRAILS” of connected PPsets.

These three simple rules, combined with the PS-Fractal Set will combine —concatenate — with another PS-Fractal Set at each subsequent PS step within a given sequence and will allow one to form the entire PTOP (Periodic Table Of PRIMES) from scratch, without any direct reference to the BIM (BBS-ISL Matrix) from which it was originally derived.

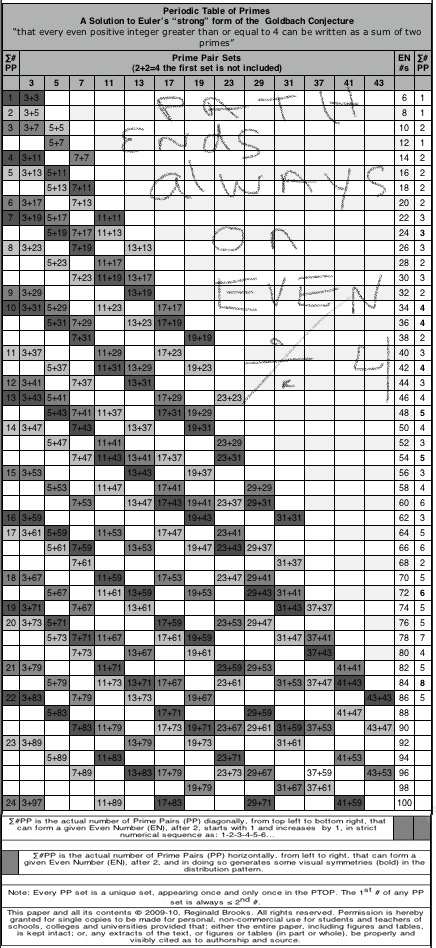
Furthermore, and not without enormous significance, the P₁, P₂ members of ANY and ALL PPsets that sum to equal an EVEN # (Goldbach Conjecture), are ALWAYS symmetrically spaced (STEPS) from either side of the said EVEN/2.

This can be seen on the PTOP by simply dividing the EVEN by 2 and observing that the PPset members are always equal STEPS away to either side, except when the TRAIL ends and P₁ = P₂.

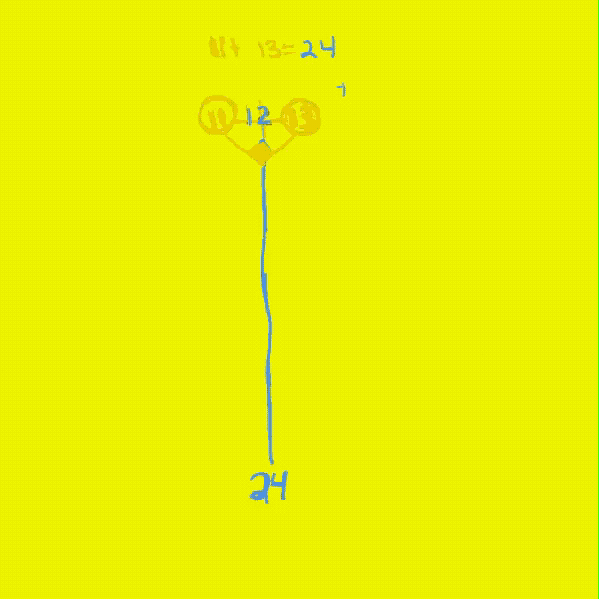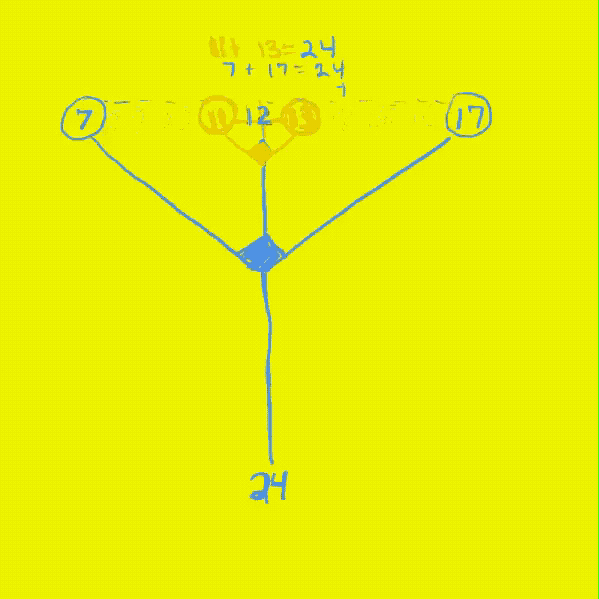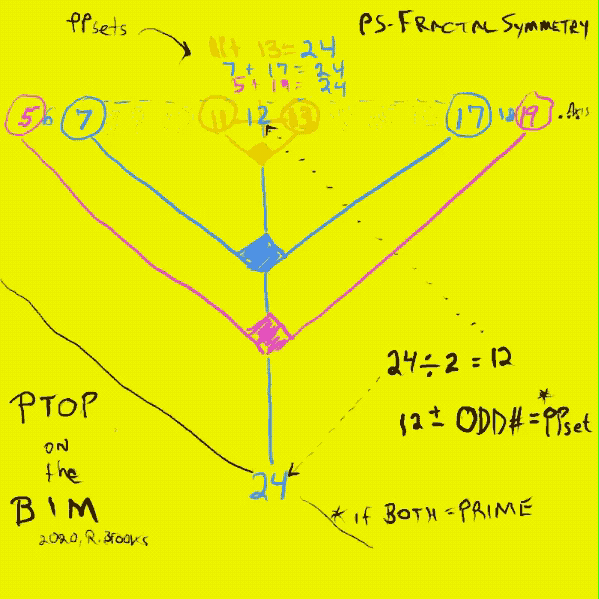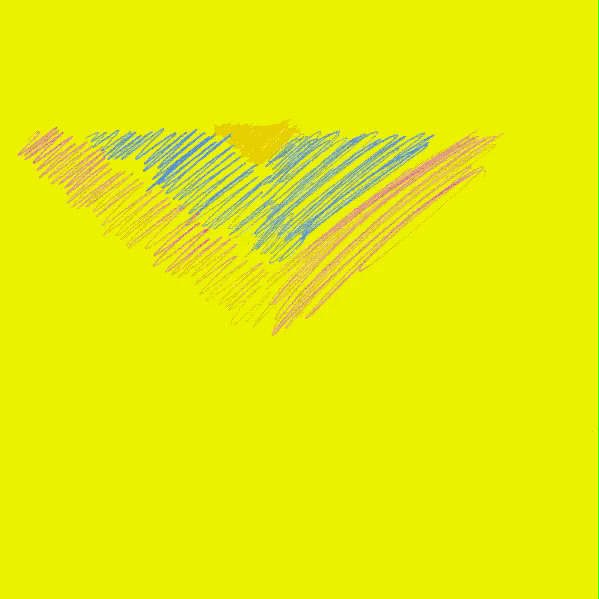
On the BIM, dividing the EVEN by 2 leads to a straight-line path to EVEN/2 on the Axis, and there one sees a very clear visual of how PPset members are always equal STEPS away to either side, except when the TRAIL ends and P₁ = P₂. Additionally, lines drawn from each respective P₁, P₂ will meet on that straight-line path at 90° forming a Right-angled isosceles triangle. All such PPsets that compose any said EVEN will have their Right-triangles on this same line.

The geometry of the PS-Fractals is clearly shown on the BIM and one could easily say is an important and inherent part of the very same Inverse Square Law (ISL) that informs the spacetime structure of the Universe!

See the PRIMES Index

Outline:

1. PTOP derived from the BIM;
2. How to Make the PTOP from the BIM;
3. Simple, fractal-based way to directly make the PTOP.

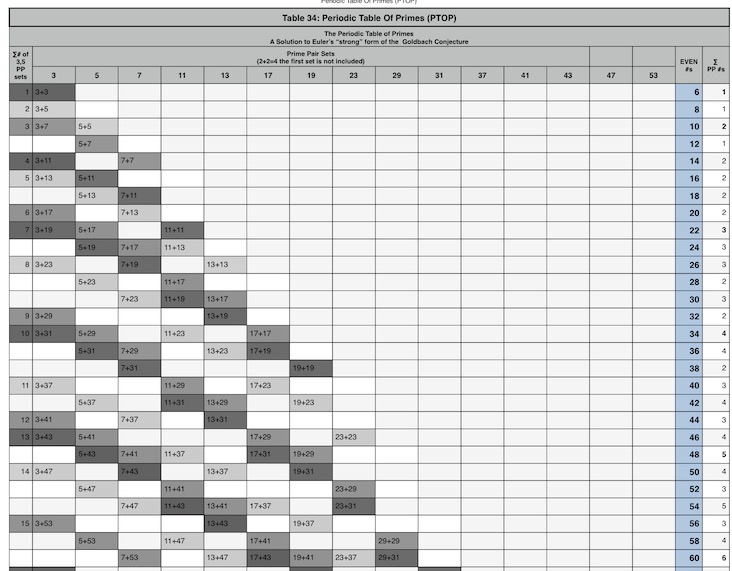
The PTOP is derived from the BIM (steps 1-10):

Proof of the Goldbach Conjecture (strong form, ≥6) (See images below text)

1. Natural (n), Whole Integer Numbers (WIN) — 0,1,2,3,…infinity — form horizontal and vertical Axis of a simple matrix grid.

2. The squares of such WINs — n²=1²=1, 2²=4, 3²=9,…infinity — forms the central Diagonal of said grid — dividing it into two bilaterally symmetric triangular halves.

3. Every Inner Grid (IG) cell within is simply the difference (∆) between its horizontal and vertical Diagonal intercept values. They extend to infinity. The Diagonal WINs form the base of a 90° R-angled isosceles triangle with said IG cell value at the apex.

4. Every IG cell within is also the product of two Axis WINs (Either horizontal or vertical, not both), that form the base of a 90° R-angled isosceles triangle with said IG cell value at the apex.

5. The complete matrix grid extends to infinity and is referred to as the BIM (BBS-ISL Matrix).The BIM forms — and informs — a ubiquitous map (algebraic geometry) to:

   • ​ The Inverse Square Law (ISL);

   • The Pythagorean Triples (PT);
   • The PRIMES (stealthily hidden, but revealed by NPS (Number Pattern Sequence).

6. The 1^st Diagonal that runs parallel to either side of the main Prime Diagonal (PD, not of PRIME numbers, but primary), is composed of the ODD WINs: 1,3,5,…infinity.

7. If we add +1 to each value, that 1^st Diagonal now becomes a sequence of ALL the EVEN WINs (≥4): 4, 6, 8,…infinity. NOTE: this is why the PTOP is hidden, in the normal, base BIM these remain ODDs.

8. Select ANY EVEN WIN and plot a line straight back to its Axis WIN — that Axis WIN = EVEN/2 = core Axis #.

9. Upon that same Axis, PRIME Pair sets (PPsets) — whose sum (∑) equals the EVEN WIN (on the 1^st Diagonal) — will be found that form the base of 90° R-angled isosceles triangle(s) whose apex lie(s) on that straight line between the EVEN and its 1/2 Axis WINs. PPsets with identical PRIMES = 1/2 Axis value.

10. The proof that every EVEN WIN has ≥1 PPsets can be seen in the Periodic Table Of PRIMES (PTOP) that stealthily informs the BIM of how each and every EVEN WIN is geometrically related to one or more PPsets.

How to Make the PTOP from the BIM (steps 1-10):

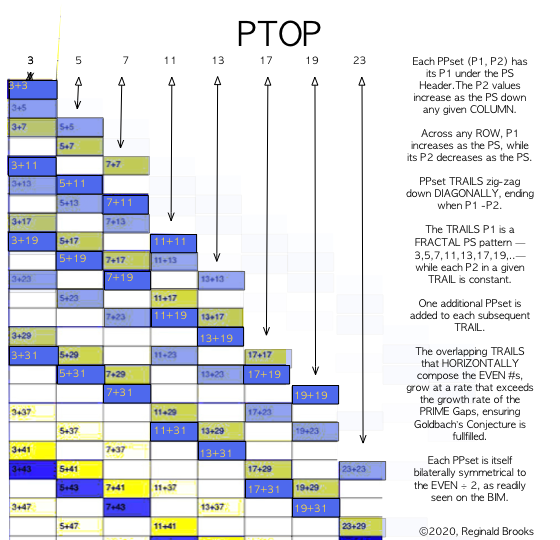
1. These PPsets are NOT randomly contributing their ∑s to equal the EVEN WINs, rather they come about as the consequence of a strict NPS: the sequential — combining, linking, concatenation — addition of the PRIMES Sequence (PS) — 3,5,7,11,13,17,19,…—to a base PS — 3,5,7,11,13,17,19,….

2. The NPS of this addition forms the PTOP: for each vertical PS — the 1^st PRIME (P₁) remains constant (3), the 2^nd PRIME (P₂) sequentially advances one (1) PS WIN — is matched diagonally with the 2^nd PS, but now the 1^st PRIME sequentially advances, while the 2^nd PRIME remains constant within a given PPset.

3. This matching addition of the 2^nd PS at the bifurcation point of the common 2^nd PRIMES, forms the zig-zag diagonal PPset Trails that are the hallmark of the PTOP.

4. For every subsequent vertical PPset match, the Trail increases by one (1) PPset.

5. The rate of such PPset Trail growth far exceeds the PRIME Gap rate.

6. The zig-zag diagonal PPset Trails combine horizontally on the PTOP to give the ∑# of PPsets whose ∑s = The EVEN WIN.

7. More than simply proving the Goldbach Conjecture, the PTOP hidden within the BIM reveals a new NPS connection of the PRIMES: PRIMES + PRIMES = 90° R-angle isosceles triangles.

8. The entire BIM, including the ISL—Pythagorean Triples—and, PRIMES, is based on 90° R-triangles!

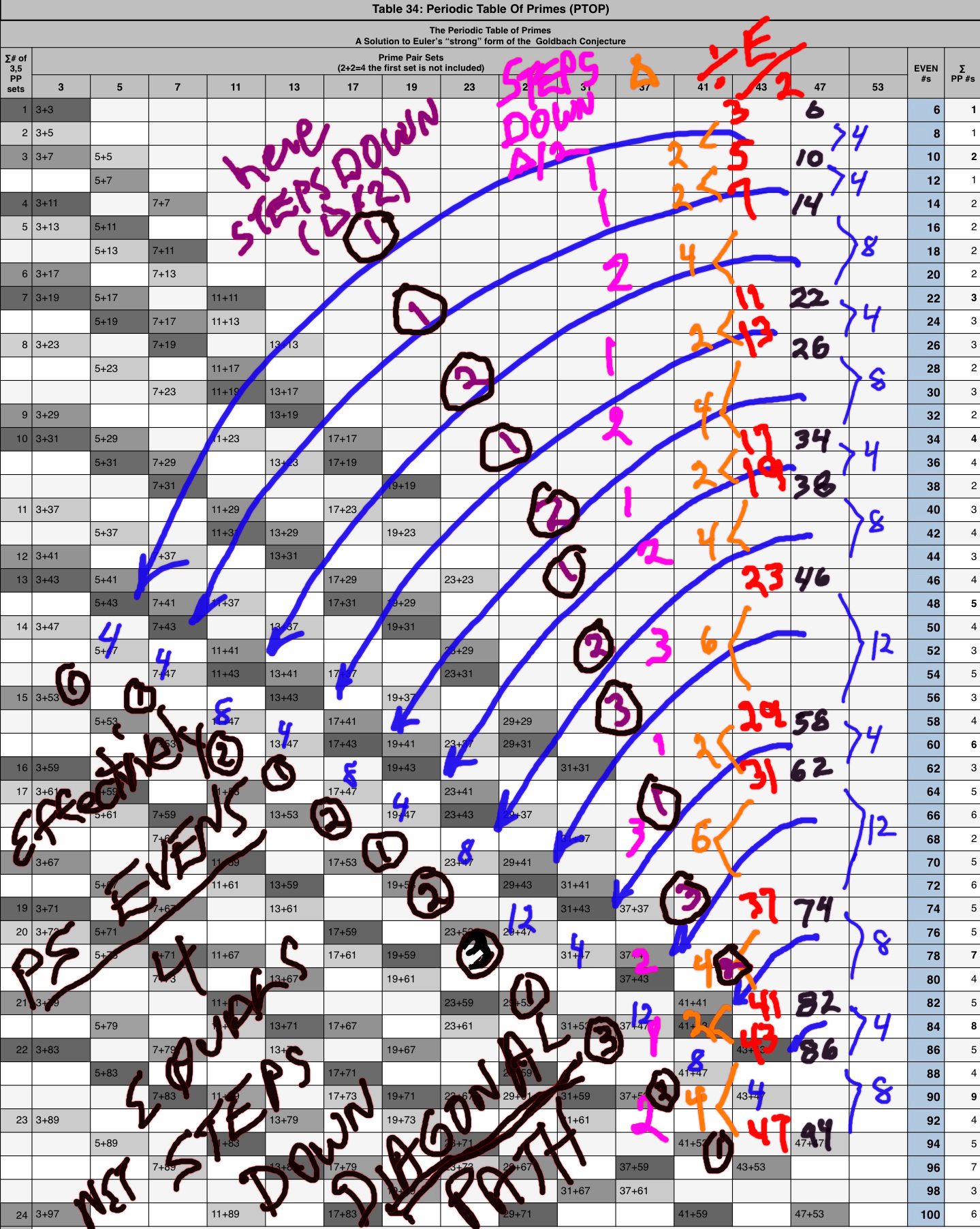
   Similar to how the grid cell values of the Axis, PD and IG of the Pythagorean Triples reveal additional, intimate connections within the BIM, so too do the PPsets: the 1^st PRIME values of each set points to the # of STEPS from the PD that intersects the given EVEN WIN (Axis²), on a straight line path back to its Axis, at the apex where its other PPset member intersects — this is no mere coincidence — and that apex is, of course, the 90° R-angle isosceles triangle that results. For example: EVEN = 24, Axis = 12, PD = 144, # of STEPS from PD towards Axis = 5 and 19 for the 5+19 PPset and 7 and 17 for the 7+17 PPset, and 11 and 13 for the 11+13 PPset that each forms the EVEN 24.

9. On the PTOP, the bifurcation concatenation of the PS — 3,5,7,11,13,17,19,..— forming the zig-zag diagonal Trail with the same vertical (Column) base PS — 3,5,7,11,13,17,19,…— of those respective EVEN WINs— that when “3” is subtracted, the remainder is a next-in-the-sequence PRIME — providing the remainder is itself NOT ÷ by 3, 5, 7, or any othe prime. Ex: 24 - 3 = 21, but 21 is ÷3, so no PS on the 24 EVEN Row. Ex: 22 - 3 = 19 and 19 is the PRIME within the PS located on that 22 EVEN Row.

10. Another set of STEPS (S) from the core Axis value directly on the BIM Axis, identifies each symmetrical pair of a given PPset that forms that given EVEN. These STEPS may by Universally calculated from the EVENS, P₁ and P₂ values. They follow a NPS on the PTOP. (See images below text).

The Simple, Fractal-based method for making the PTOP (steps 1-5):

1. Place the PS along the Columns Header of your table (3,5,7,11,13,17,19,…53), ending with the EVENS #s header. If you like, you can also add the Sum (∑) PP #s header: the # of PPsets that make that EVEN.

   

2. Make a header Column on the far left side of the table for the ROWS Header, labeled ∑# of 3,5 PP sets and fill it in vertically down that Column with the natural number sequence (1,2,3,..) but leaving BLANK any Gaps in the PS: thus 1,2,3, BLANK Gap (for 9), then 4,5, BLANK Gap (for 15), then 6,7, BLANK Gap (for 21), then 23, BLANK Gaps (for 25,27), then 29,31, BLANK Gaps (for 33,35), then 37,… These #s reveal the length of the PPset Trails. The BLANK Gaps 9,15,21,.. are for the NON-Prime #s place holders.

   

3. Now, for the really easy parts: Under Column Header 3 — and matching the entries in the Vertical Row Headers you just made above — enter 3+P₂, where P₂ is the PS (3,5,7,11,13,17,19,…). Here the PS is a fractal presented in a vertical array, with the P₁ value being a constant 3.

   

4. The SAME PS fractal above is now going to form the rest of the table! Only now, its array will be skewed, forming a zig-zag diagonal. This diagonal will exactly follow the PS, only it will be skewed such that diagonal corner of PS 3 will go over 1 step and down 1 step to locate PS 5. PS 5 will go over 1 step, down 1 step to locate PS 7. Now, because there is a Gap of one (ODD#) between PS 7 and PS 11, one must from PS 7 go over 1 step, and down 2 steps to locate PS 11. This is the fractal-based NPS of the PS and once you get the pattern down, it is simple repeated identically starting at each PPset in the Rows under the Column Header 3. The only caveat is that the PPset Trail so formed truncates when P₁ = P₂.

   

   

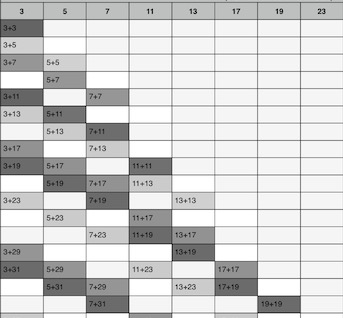
5. Is quite helpful, but not required, to give some form of repeating graphic background tone to more clearly designate each PPset Trail, e.i. dark-light-med-dark-light-med.
   

   Remember: every Trail is made of exactly the SAME Fractal Pattern: steps down from the 1st PPset (Column 1) —↓1—↓1—↓ 2—↓1— ↓2— ↓1—↓2—↓3—↓1...

Images, Animations and Videos

Path ALWAYS ends on EVEN NOT ÷ 4.

Start and End of TRAIL

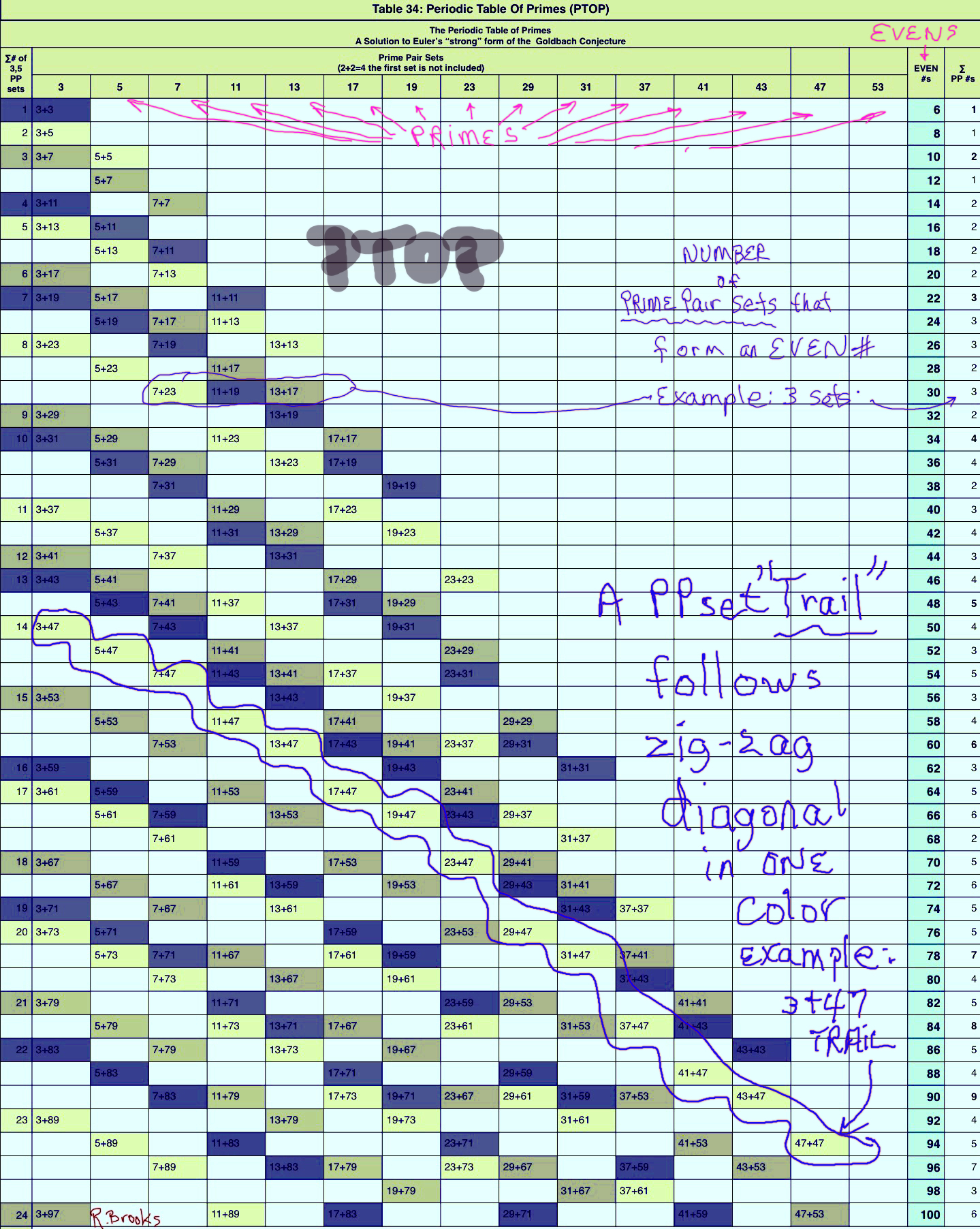PPset Trail follows a zig-zag diagonal down the PTOP.

The PPset TRAILS ALWAYS follow the same PS pattern, adding 1 new set for EACH vertical PS PPset.

As the PPset TRAILS grow, their overlap ensures that ALL EVENS are composed of the sums of one or more PPsets.

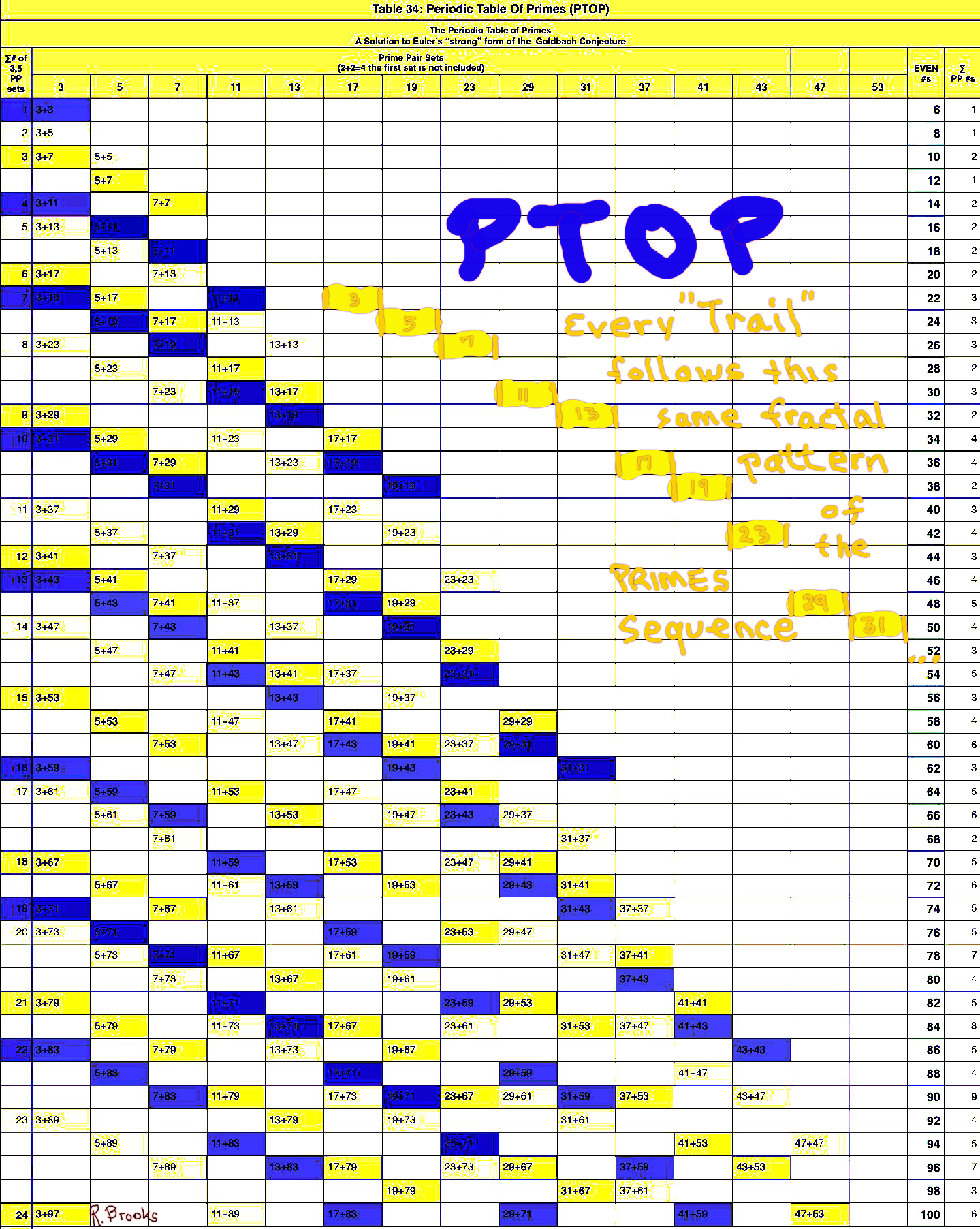Every PPset TRAIL follows the exact same PS-Fractal pattern.

Every PPset TRAIL follows the exact same PS-Fractal pattern: the steps – gaps – between subsequent PRIMES is fixed as 1-1-2-1-2-1-2-3-1...

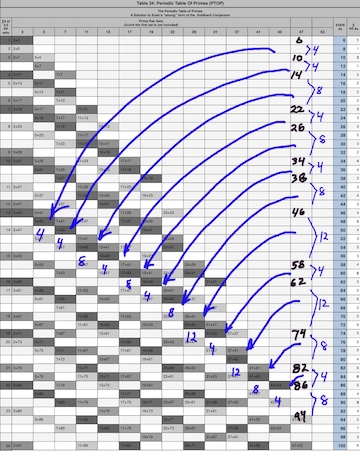Here we see that the differences (∆) between the EVENS that correspond to the END of the PPset TRAILS (P₁ = P₂). Dividing the ∆/4 = PS steps pattern.

Or we can simply take the differences (∆) between the EVENS at the TRAIL Ends directly and ÷ by 2 = PS steps sequence: 1-1-2-1-2-1-2-3-1… Effectively, the PS EVENS/4 = net steps down the Diagonal TRAIL.

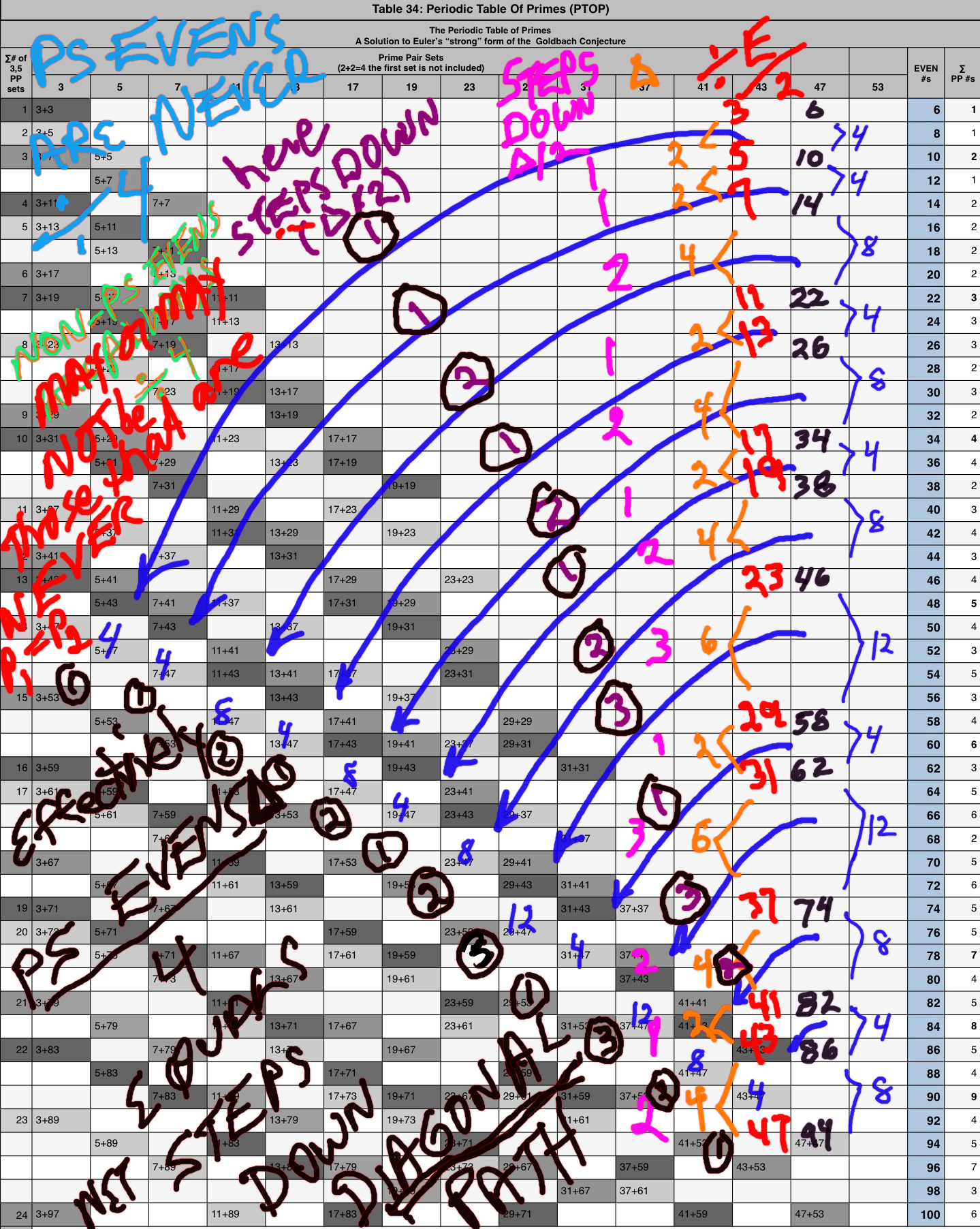The RULE is that the PS EVENS are NEVER ÷ 4, while the NON-PS EVENS may or may not be ÷4, and those that are, are NEVER at P₁ = P₂ TRAIL Ends.

Summary I.

Summary II.

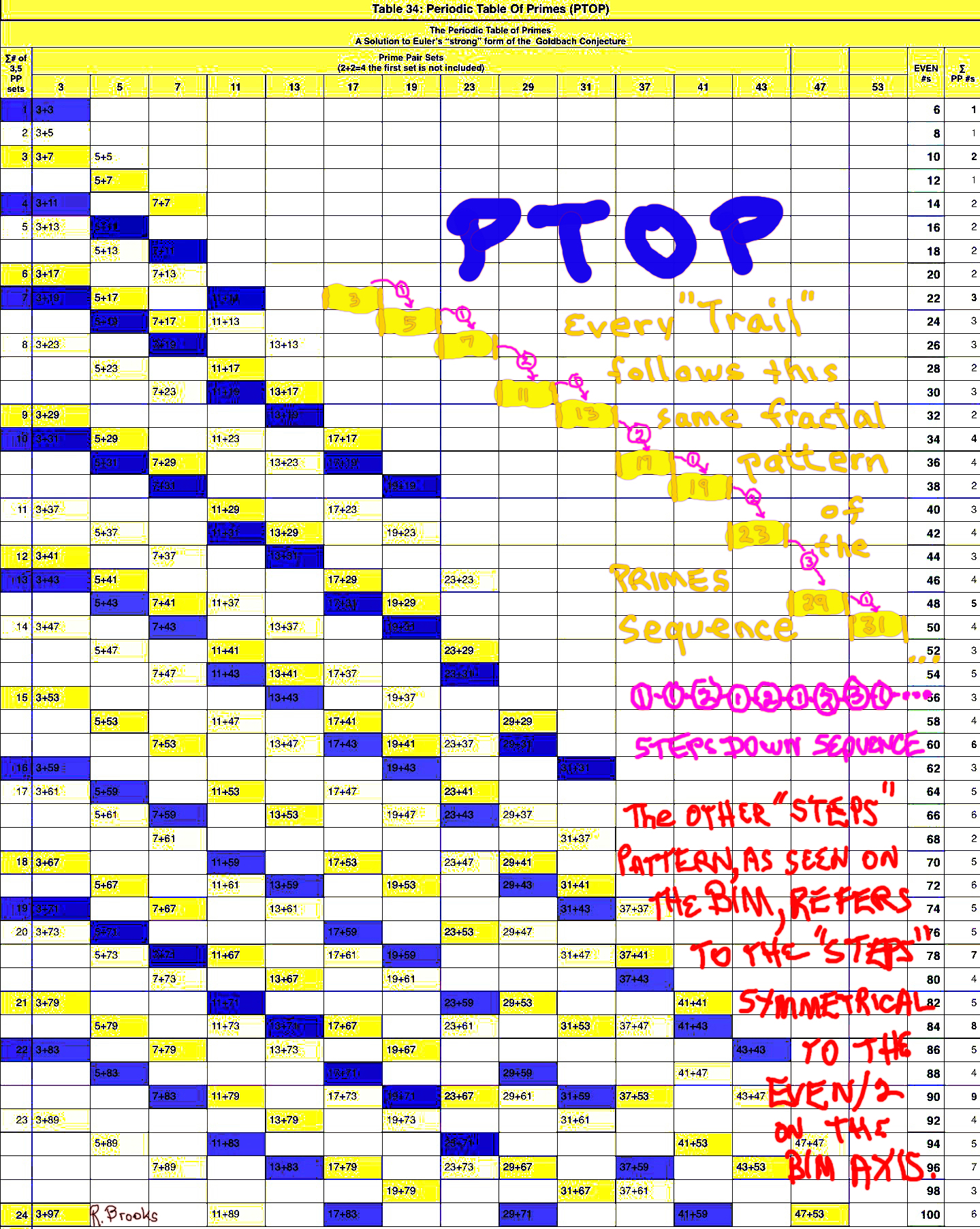
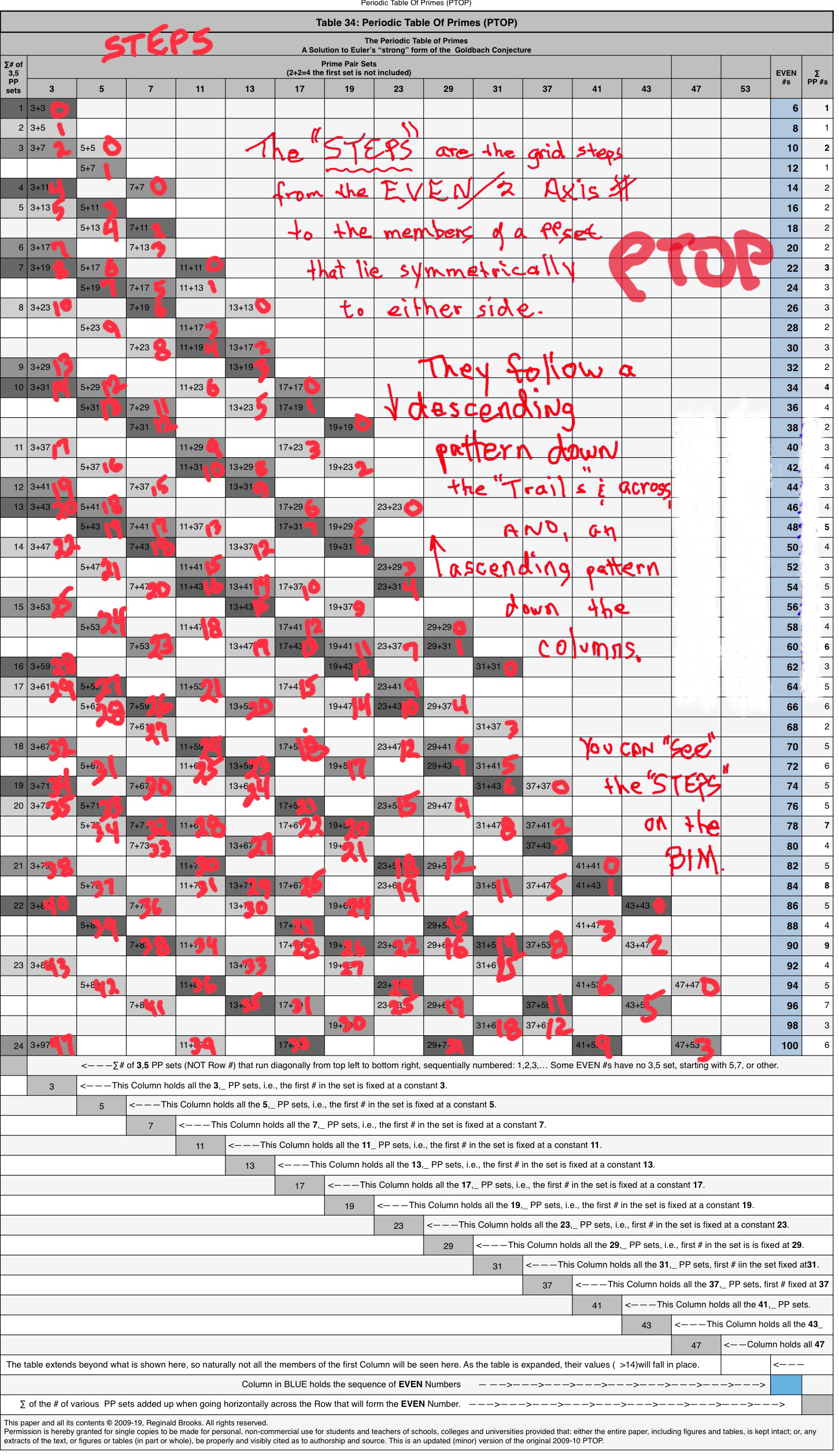The "STEPS" – not PS "steps" between the PRIMES – are the grid STEPS from the EVEN/2 Axis # on the BIM to the respective members of a PPset that lie symmetrically to either side. They follow a descending pattern down and across the TRAILS, and, an ascending pattern up the Columns. The PTOP is best for the summary pattern, while looking directly at the BIM is best for seeing the individual pattern(s).

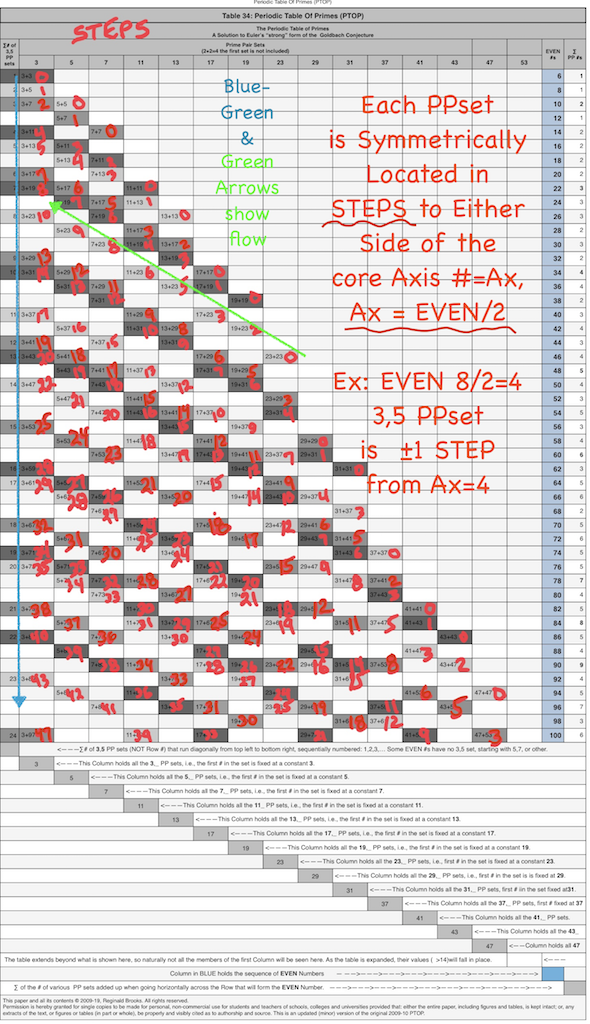
Summary III. While the PTOP is "hidden" – i.e. not immediately obvious – on the BIM, with a slight tweak to the 1^st Parallel Diagonal raising each ODD to an EVEN, the straight-line path back to the Axis points to the core Axis value of that EVEN. To either side, the members of the PPset(s) forming said EVEN, are symmetrically found as identical steps to either side. A line diagonally back from the PPset members forms at the intersection of straight-line path a 90° Right isosceles triangle. We have then, two forms of the fractal: the PS-Fractal that informs the spacing of the PPset TRAILS, and, the Fractal-Right-isosceles-triangle that presents each PPset on the BIM.

Summary IV.

Summary V.

Summary VI.

PTOP & Goldbach Conjecture from Reginald Brooks on Vimeo.