New PTOP on the BIM
PREFACE
Fractal — Symmetry — Inverse Square Law (ISL). These are not the usual descriptive terms associated with the Prime numbers (PRIMES) Yet that is exactly what best describes the PRIMES!
The PRIMES, when brought together as P1 & P2 members of PRIME Pair Sets (PPsets) demonstrate a robust symmetry and an intimate relationship with the ISL when shown on the BIM (BBS-ISL Matrix grid of the Inverse Square Law). This symmetry is brought out in the geometric relationship between the PPsets and the EVEN numbers (EVENS) that they inform consistent with Euler’s Strong Form of the Goldbach Conjecture.
This come about as the well established PRIMES Sequence (PS) — 3-5-7-11-13-17-19-23-29-31-... acts in a fractal-like manner, i.e., it demonstrates redundant, repetitive and re-iterative behavior in presenting self-similar reflection of itself as it constructs PPsets and PPset “TRAILS.”
The TRAILS are formed from the concatenation of PS’s progressively onto each successive PRIME of a given PS — forming a series of PPsets along the way. The TRAILS can also be seen to be formed directly as individual PPsets on the BIM. Here, each PPset is easily seen to be intersection of 1 PPset member from the Horizontal AXIS and 1 PPset member from the Vertical AXIS, together forming the P1, P2 members. The TRAIL is simply all those PPsets thus formed across a Row — or down a Column — on the bilaterally symmetrical BIM. All this is easily visible on the BIM.
That leads us to our story about the PRIMES—Fractals—Symmetry—and the intimate relationship they have with the ISL as seen on the BIM.
ABSTRACT/DESCRIPTION
ABSTRACT
The “PTOP (Periodic Table Of PRIMES) & the Goldbach Conjecture” (2019), also referred to as BIM: Part I, updated and clarified the PTOP, PPsets and their PPset TRAILS that were originally presented in MathspeedST (2010). BIM = BBS-ISL Matrix.
In this work, a major update and refinement has been made. Each of the three parts — BIM: II, III and IV presents new findings that visibly demonstrate the PRIMES on the BIM.
Each and every PRIME, when treated as part of a PPset (P1, P2), can be found and individually profiled DIRECTLY on the BIM as seen in BIM: Part II.
Plotting all the Lower Diagonal P2 PRIMES on a table and then re-plotting those results back onto the BIM opened up a new vista. By substituting the AXIS values for each of those P2 PRIMES from the table, one has now formed a new SubMatrix of the BIM with ALL the PPsets in place — BIM: Part III.
In BIM: Part I-III, we have mostly used just half of the bilaterally symmetric BIM to reveal and describe the geometry.
In BIM: Part IV, we now look at the whole BIM with the PPset SubMatrix in place.
Treating these PPsets as objects and counting them within progressively larger square areas — forming what is called “Object AREAS” — a pure ISL Number Pattern Sequence (NPS) is found. As the PS-Fractal series of each AXIS joins to form the PPsets, their actual numbers — as PPset TRAILS — progressively grows and sums up to quantities with Object AREAS that directly mirror the fundamental ISL NPS: 1—4—9—16—25–…
And while this intimate relationship of the PRIMES to the ISL can not predict the next largest PRIME, it can ABSOLUTELY account for each and every PRIME at, and below, any given PRIME, regardless of size.
While Euler’s Strong Form of the Goldbach Conjecture is proved along the way, the real significance is what we have seen unfolding in BIM: Parts I-IV. The role of Symmetry and Fractal underlie everything about the PRIMES.
The PRIMES on the BIM is all about how the fractal nature of the PS becomes expressed as symmetry on the BIM as isosceles and equilateral triangles, forming the PPsets that ultimately form ALL the EVEN numbers!
What is marvelous, incredible, mind-blowing in every way, is that this same symmetry—fractal—isosceles/equilateral triangle relationship is found — indeed, is part and parcel — throughout the BIM.
The ISL seems to reflect the most basic and fundamental relationship(s) between quantity and the numbers that account for it.
DESCRIPTION
SYMMETRY, STEPS, EVENS, EVENS/2, PPsets, PRIME SEQUENCE FRACTALS, ISOSCELES & EQUILATERAL TRIANGLES, INVERSE SQUARE LAW, PYTHAGOREAN TRIPLES; ALL ON THE BIM (BBS-ISL Matrix).
In MathspeedST, the PRIMES were found to be stealthily hidden within the BIM, revealing their presence ONLY when the BIM itself had its ODD #s 1st Parallel Diagonal modified to EVENS by the addition of 1 to each ODD.
This resulted in the original PTOP (Periodic Table Of PRIMES) on the BIM. It was refined by pulling the values off the BIM and making a separate PTOP. All this became the subject of “PTOP (Periodic Table Of PRIMES) & the Goldbach Conjecture” ebook and white paper (2019). It is also referred to as BIM: Part I. The PPsets and their TRAILS were introduced.
Each and every PRIME, when treated as part of a PPset, can be found and individually profiled DIRECTLY on the BIM. BIM: Part II was formed.
Plotting all the Lower Diagonal P2 PRIMES on a table and then re-plotting those results back onto the BIM opened up a new vista. By substituting the AXIS values for each of those P2 PRIMES from the table, one has now formed a new SubMatrix of the BIM with ALL the PPsets in place.
This is a direct consequence of locating the PPsets as the grid space resulting from the intersection of the PRIMES Sequence (PS) of the Horizontal AXIS with the PS of the Vertical AXIS. This becomes the basis for the BIM: Part III.
In BIM: Part I-III, we have mostly used just half of the bilaterally symmetric BIM to reveal and describe the geometry.
In BIM: Part IV, we now look at the whole BIM with the PPset SubMatrix in place.
What we find is that by treating these PPsets as objects and counting them within progressively larger square areas — forming what is called “Object AREAS” — a pure ISL Number Pattern Sequence (NPS) is found. Yes, as the PS-Fractal series of each AXIS joins to form the PPsets, their actual numbers — as PPset TRAILS — progressively grows and sums up to quantities with Object AREAS that directly mirror the fundamental ISL NPS: 1—4—9—16—25–…
And while this relationship of the PRIMES to the ISL can not predict the next largest PRIME, it can ABSOLUTELY account for each and every PRIME at, and below, any given PRIME, regardless of size.
While Euler’s Strong Form of the Goldbach Conjecture is proved along the way on this journey, the real significance is what we have seen unfolding in BIM: Parts I-IV. The role of Symmetry and Fractal underlie everything about the PRIMES.
The PRIMES on the BIM is all about how the fractal nature of the PS becomes expressed as symmetry on the BIM as isosceles and equilateral triangles, forming the PPsets that ultimately form ALL the EVEN numbers!
What is marvelous, incredible, mind-blowing in every way, is that this same symmetry—fractal—isosceles/equilateral triangle relationship is found — indeed, is part and parcel — throughout the BIM.
The ISL seems to reflect the most basic and fundamental relationship(s) between quantity and the numbers that account for it.
Introduction
The PRIMES have been found on the BIM despite there being NO PRIMES in the Strict Inner Grid (SIG). The SIG is simply the BIM without the AXIS, Prime Diagonal (PD) that runs diagonally down the middle, dividing the grid into two bilaterally symmetrical triangular halves, and, the 1st Parallel Diagonal of ALL ODD numbers.
So where are they?
BIM: Part I and the original PTOP
Initially, they were found in a quasi-stealth mode on the BIM. Why quasi-stealth? The PRIMES were naturally found on the AXIS (n=1,2,3,…). It was only when they were paired symmetrically to either side of another AXIS #—a number that turned out to be an EVEN ÷ 2— that the lines of the triangular sides (diagonals) meet on a line from said EVEN ÷2 # on the AXIS, back to the 1st Parallel Diagonal. Yes, here we had to use the entire BIM, and, that 1st Parallel Diagonal had to have ALL its ODD #s advanced (+1) to make them EVEN.
From this, it was found that every EVEN # on the adjusted 1st Parallel Diagonal, had, indeed, one or more sets, or pairs, of PRIMES on either side of the EVEN/2, found on the AXIS.
Visually, this demonstrated that every EVEN was flanked by one or more pair sets of PRIMES. We call these PPsets and each contains a P1 and P2 value that resides symmetrically on either side of the EVEN/2 AXIS #. The only exception being when P1 = P2, then the symmetry is one, i.e., EVEN = 10 has EVEN/2=5 and there are two PPsets that inform EVEN = 10 are 3,7 and 5,5.
Visually, this also demonstrated both the symmetrical nature of the PPsets and the isosceles, right-triangle each made pointing back to the line connecting the EVEN with its EVEN/2 AXIS #.
This early (discovered in 2009–10) “PRIMES on the BIM” will be referred to as BIM: Part I.
A simplification of BIM: Part I formed the basis of the PTOP (Periodic Table Of PRIMES, as first described in MathspeedST, 2010).
The PTOP extracts the PPsets and EVENS from the BIM and relates them to each other in a straightforward and graphical manner.
A distinct PPset “TRAIL” is seen for each PPset starting with the P1=3 and P2 = each successive number in the natural PRIMES sequence—(2),3,5,7,11,13,17,19,23,29,31,37,…
In fact, this natural PRIMES Sequence (PS) acts in every way just like a fractal, whereby a fractal set consisting of the PS is “added” —i.e. concatenated—to each successive P1 value down the Column 3 on the PTOP.
This fractal PS property ensures that there are more overlapping “TRAILS” of PPsets than PRIME Gaps, ensuring that ALL EVENS = the sum of two PRIMES. Euler’s Strong Form of the Goldbach Conjecture is proven. More importantly, a definitive relationship between PRIMES and the Inverse Square Law is defined. This joins the ISL, Primitive Pythagorean Triples and PRIMES together under the umbrella of the Inverse Square Law as presented on the BIM. Part I and the original PTOP is fully described in both the white paper and ebook: PTOP (Periodic Table Of PRIMES) and the Goldbach Conjecture (2019). PRIMES Index.
BIM: Part II
In BIM: Part II, the focus was shifted to looking at individual PPsets on the BIM—those making one EVEN number at a time. It is quite interesting how once again those stealthy PRIMES only appear on the AXIS and 1st Parallel Diagonal, yet make a clear, distinctive Number Pattern Sequence (NPS) by their interactions.
In this case, for every EVEN/2 on the AXIS, an isosceles triangle is formed with the base along the AXIS, one side along the PD to the apex of the (EVEN/2)2 and the other side back to the base on the AXIS.
The PPset P1s are found on the Upper Diagonal PD as the √ of where the PS # on the AXIS intersects the PD—there the square root of that PD #=P1, or more easily, just take its Axial value.
The Lower Diagonal (LD) ALWAYS points back to the EVEN on the AXIS. Along the way, it intercepts with the PS values on the AXIS above, to give the P2 values. Dividing the various grid values along the LD by 4x(Even/2) will select out and confirm which values house the P2 PRIMES.
Incredibly, it turns out the number of STEPS from one apex to another around each of the triangles formed, will show them to ALWAYS be equal, thus equilateral. The larger base:PD:LD isosceles triangle is actually made of two equilateral triangles positioned back-to-back with the centerline being the line from the EVEN/2 back to it squared value on the PD.
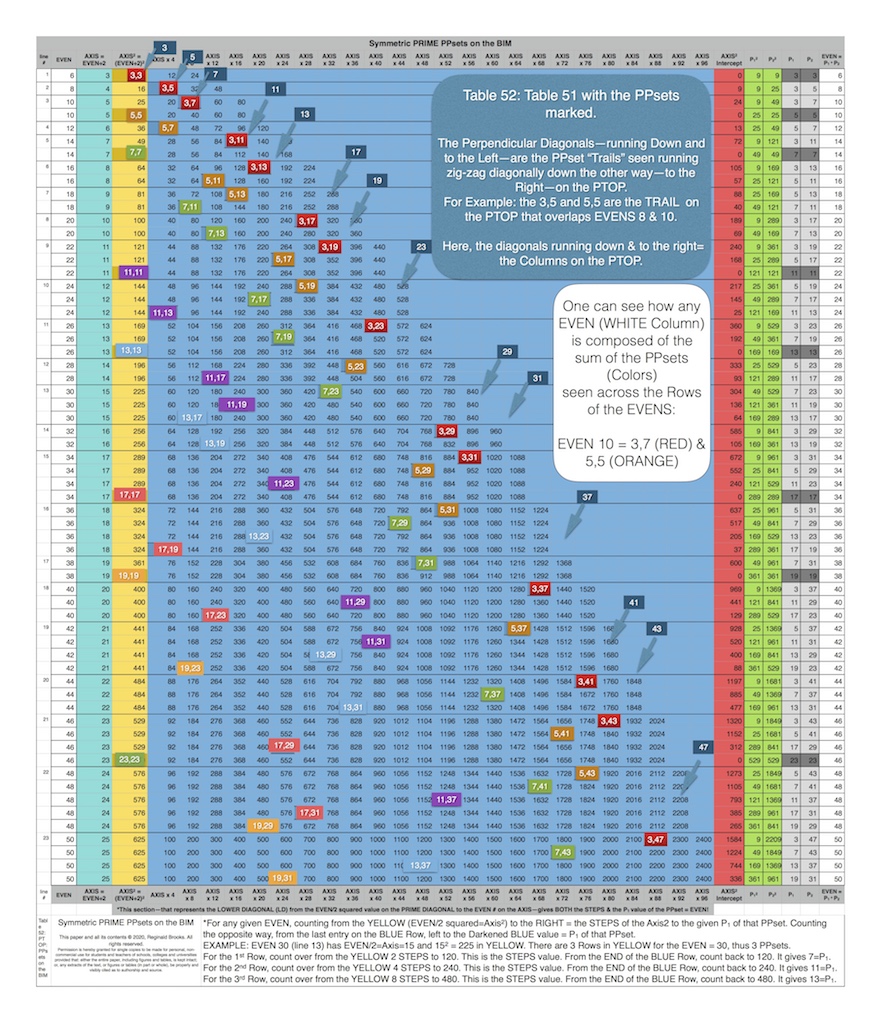
Table 51 was formed by plotting all the LD values for each EVEN as seen in BIM: Part II. These values were then plotted back on to the BIM and BIM: Part III was formed.
BIM: Part III
In Part III, we combine and simplify everything from the Part I & II including:
SYMMETRY, STEPS, EVENS, EVENS/2, PPsets, PRIME SEQUENCE FRACTALS, ISOSCELES & EQUILATERAL TRIANGLES, INVERSE SQUARE LAW, PYTHAGOREAN TRIPLES; ALL ON THE BIM.
~~~~~~
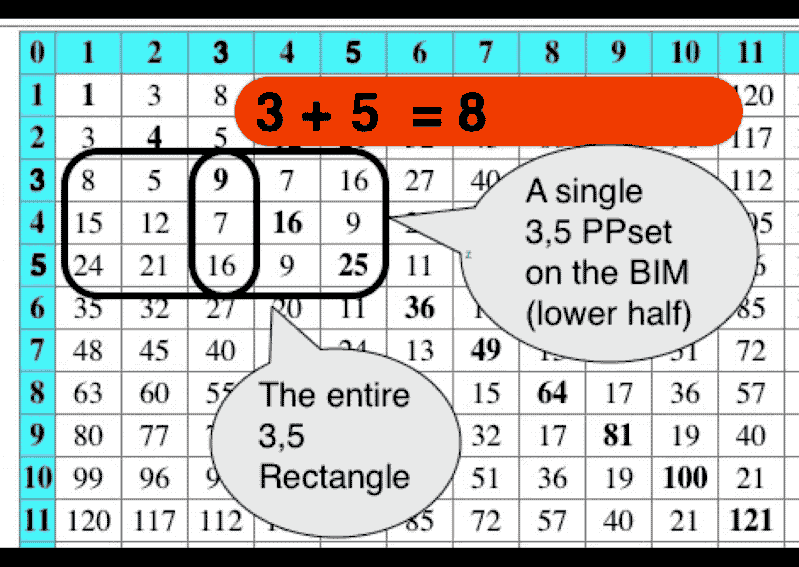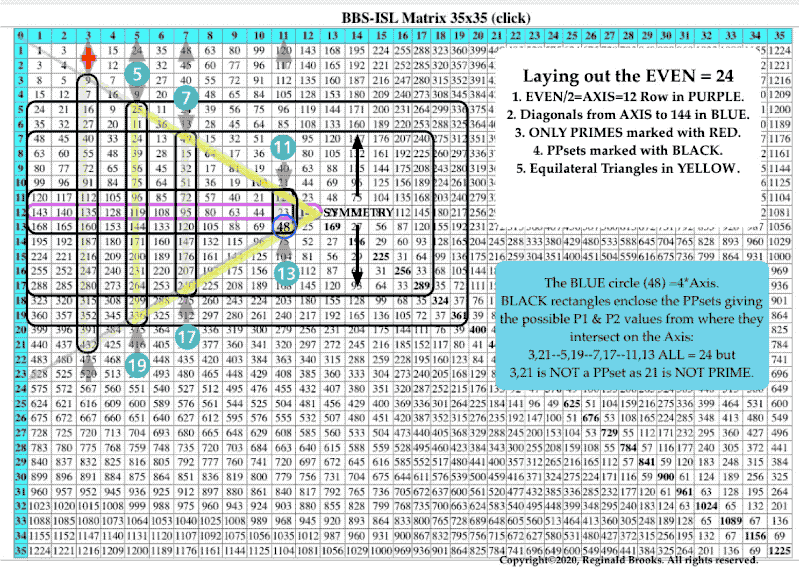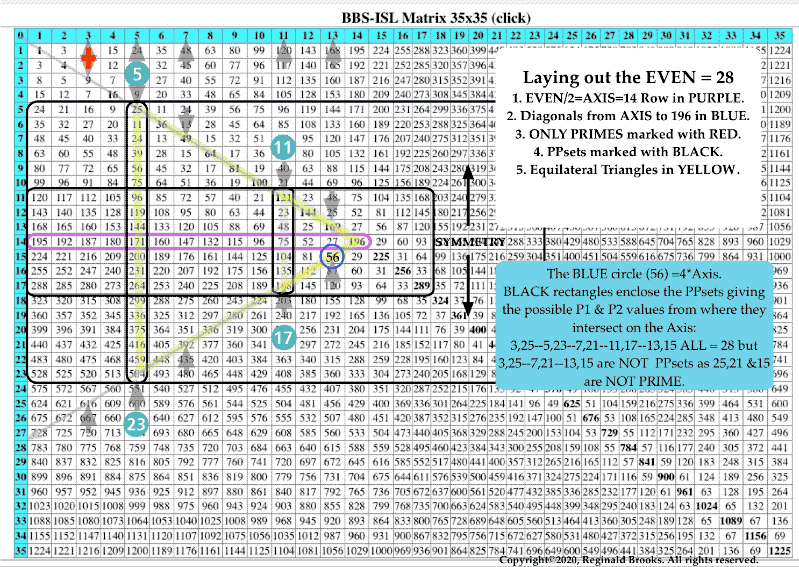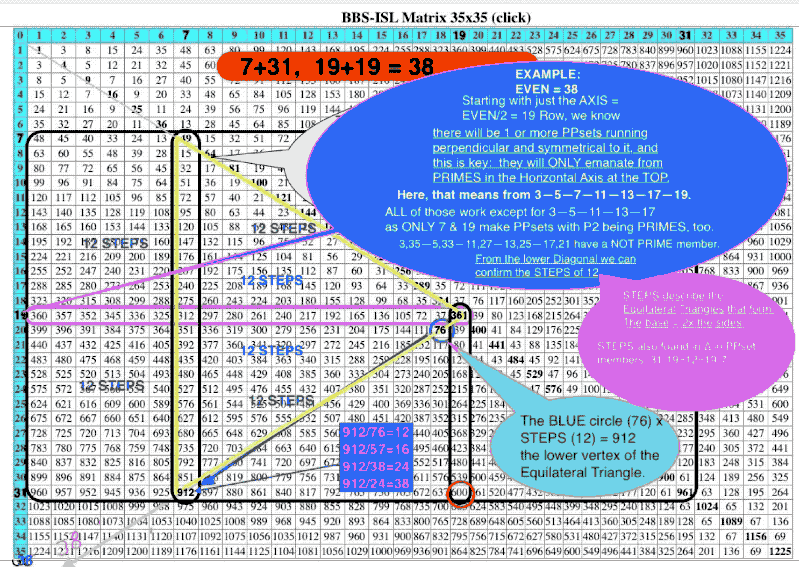
These PPsets are formed from the Horizontal and Vertical AXIS numbers that intercept those BLUE circle values. The PRIMES Sequence (PS)—3,5,7,11,13,17,19,23,…— determines the pattern. Notice that the PPsets ALSO fall exactly on the same BIM/24 Active ROWS (PURPLE Bands) as do the PPTs and PRIMES
Those BLUE values from Table 51 are now BLUE CIRCLE values on the BIM. And when those values are overlaid with the PPsets it now becomes Table 52 and the NEW PTOP (Periodic Table Of PRIMES) on the BIM! Here they are plain and simple. Let the story begin.
Like shining a light at a sculpture in the dark, each angle reveals a new “look,” yet it is just one sculpture. That’s what we are doing here..
BIM: Part III becomes significant when one finds that the NPS of those PPsets falls on exactly the SAME Active Rows that previously ALL PRIMES and ALL PPTs were found to occupy on the BIM! No small coincidence and quite easily seen when, as in Table 52, the actual PPset values are overlaid on those LD values. The PS fractals along the Horizontal and Vertical AXIS intercept at these points on the BIM. They form the NPS of the PTOP directly on the BIM! It is no longer hidden!
The PRIMES Sequence Fractal—3–5–7–11–13–17–19–23–29–31-…—found along each AXIS, together forms the PPsets = EVENS = Goldbach Conjecture Proof.
The PPset TRAILS (Rows) ALWAYS INCREASE FASTER than the PRIME Gaps ensuring that the PPsets = EVENS = Goldbach Conjecture Proof.
One could say, that by definition, ALL EVENS are indeed formed from the OVERLAPPING PS Fractal TRAILS of PPsets = EVENS = Goldbach Conjecture Proof.
~~~
EVEN = 30
EVEN/2 = 15
7, 23 = 7 + 23 = 30
23 - 7 = 16
16/2 = 8
8 = STEPS to either side of 15 as:
8 + 15 = 23
15 - 8 = 7
11,19 = 11 + 19 = 30
19 –11 = 8
8/2 = 4
4 = STEPS to either side of 15 as:
4 + 15 = 19
15 - 4 = 11
13, 17 = 13 + 17 = 30
17 - 13 = 4
4/2 = 2
2 = STEPS to either side of 15 as:
2 + 15 = 17
15 - 2 = 13
EVEN = 30 = 3 PPsets = (7, 23), (11, 19), and (13, 17)
The 3 PPsets—(7, 23), (11, 19), and (13, 17)—result from the overlap of
3 PPset TRAILS: starting at (3, 17), (3, 19) and (3, 23) PS Rows.
The TRAIL overlap occurs under the
7, 11 and 13 PS Columns, respectively.
One can see that combining the P2 PS Row values with the P1 PS Column values gives the
PPsets = (7, 23), (11, 19), and (13, 17).
And, of course, the symmetrical STEPS between the P2 - P1 values follows as shown.
It also follows that taking half of the difference in sums of the P2 - P1 = the sums of STEPS.
[(17 + 19 + 23) - (7 + 11 + 13)] ÷ 2 = STEPS = 14 = 2 + 4 + 8 STEPS.
These STEPS are BOTH the number of steps from the PD to each P1 or P2, and,
the number of steps from the P1 or P2 to the center Core Axis Value (EVEN/2) line — the line, or ROW, that connects the EVEN/2 on the AXIS to the square of the EVEN/2 on the PD.
EVEN/2 = 15 and Row 15 line intersects and terminates on the PD at (EVEN/2)2.
The NPS holds true for ALL PPsets that together define any given EVEN!
Summary of the math:
let E = EVENS, V= Value of grid cell
Like shining a light at a sculpture in the dark, each angle reveals a new “look,” yet it is just one sculpture. That’s what we are doing here. Hopefully, the BIM: Part III look will give us the simplest, most direct and informative view of just how EVERY EVEN IS MADE OF SYMMETRY AND PS FRACTAL ENDOWED PPsets IN THE FORM OF THEIR OVERLAID PPset TRAILS. Euler’s Strong Form of the Goldbach Conjecture simply falls out from this builtin relationship between the ISL, the PPTs and PRIMES as seen on the BIM.
BIM: Part IV
In closing out the “PTOP (Periodic Table Of PRIMES) on the BIM: Parts I, II and III,” one may ask if that is it it?
The hidden PTOP (Part I) was visibly profiled as individual PPsets (Part II), and the two combined to be fully revealed in plain sight in Part III. But is that it?
Besides showing that the Primitive Pythagorean Triangles, PRIMES and the PPsets and their PPset TRAILS were ALL similarly located on specific Active Rows on the BIM—Rows identified by dividing the BIM Inner Grid cell values evenly by 24—all the EVENS were shown to be informed by the PPsets. These PPsets were themselves informed geometrically by the symmetry and PRIMES Sequence (PS)-fractal nature of the PRIMES patterning in their very formation. The PS is a fractal that interacts dynamically with other PS-fractal iterations that together form the PTOP.
But is that it? Is that all? Is there something more these PRIMES can tell us about the basic numbers that inform the Universe?
Most of the graphics on the PTOP on the BIM have focused on looking at just one side of the bilaterally symmetric BIM square—and often that “square” has been stretched into a rectangular format to accommodate both the ever-increasing larger numbers and some just plain, simplified space-shapes to present info and comments on.
But what about looking at the whole BIM? In doing so, we find that the AREAS enclosed by looking at both of the bilaterally symmetric sides of the BIM gives us some NEW INSIGHTS into just what is the relationship of the PRIMES to the ISL (Inverse Square Law) ?
In “PTOP (Periodic Table Of PRIMES) on the BIM: Part IV” we will be doing just that.
Here is an older graphic, now overlayed with the NEW PRIMES-PPsets. Take all the Inner Grid cell values on the BIM that divide evenly by 24, color them YELLOW-ORANGE, and this is what you get. It showed that the Primitive Pythagorean Triangles (PPTs) always and exclusively fell on the Active ROWs—where the 1st Col. values were either YELLOW or ORANGE. Turns out the SAME is true for the PRIMES. They, too, only land on the Active ROWs. Note: some Active ROWs have neither PPT or PRIME, some have both, and some one but not the other.
Notice the pattern unfolding when the PRIMES Sequence (PS)-Fractals—3–5–7–11–13–17–19–23–29-…—from the horizontal and vertical AXIS combine on the BIM. Soon we will be looking at this pattern across the entire BIM grid.
Clarifications: The BIM is NOT a traditional multiplication table. NO WAY. While the central Prime Diagonal (PD) does represent the squares of the AXIS #s, ALL the Inner Grid (IG) values are determined by the difference (∆) in their horizontal and vertical PD intercept values, ei., 16 is PD 25 - PD 9 (25–9=16).
That said, in the PPsets as presented in the PTOP on the BIM, we will go from this standard approach, to overlaying key matrix values with the coordinates of their AXIS, i.e., 9 is overlaid with AXIS 3, AXIS 3 or simply 3,3 and 16 is overlaid with 3,5 and so on. This forms a “Sub-Matrix” on the BIM of overlaid values that will be quite useful. Once you see how simple this overlay is, a great simplification overall will reveal itself.
One other note: the PPsets as 3,3–3,5–5,5–… form the EVENS by adding the set members, i.e. 3,3 = 3 + 3 = 6, and, a diagonal line from a given PPset back to the AXIS will reveal that EVEN.
Object AREAS:
AREAS — as Object Areas — are introduced here. Object Areas simply are the # of objects within an “area.” Here that AREA is a square on the BIM. Counting the # of objects within each AREA will give the number. More surprises await.
The PPset Areas are NOT traditional areas. Instead, they represent the number (#) of PPsets captured within the boundaries of the squared AXIS #s, i.e., the squared values of the PS-fractal 3–5–7–11–13–17–19–23–29-… are 9–25–49–121–169–289–361–529–841-… but they are represented, as a “Sub-Matrix” on the BIM, as 3,3–5,5–7,7–11,11–13,13–17,17–19,19–23,23–29,29—…PPsets.
It is the # of these PPsets within the squared PS-fractal AXIS value treated as area. One is really capturing the # of “objects” or Object AREAS.
This IS a different way of capturing the way the PRIMES as PPsets are part of the BIM ISL 1–4–9–16–25-… pattern!
This way of capturing the # of objects is NOT limited to the PPsets, but rather is a natural characteristic of the BIM. Other non-prime or prime with non-prime mixtures of objects can be shown to also demonstrate this ISL pattern. It is simply the result of progressively adding 1,2,3 or more objects — in any interval — regularly to the squared AREA. It will naturally generate an ISL pattern. This points, again, to the larger role that the ISL relationship of numbers—as shown in the BIM—encompasses the expression of “other” number systems like the PPTs, PRIMES, and, any regular, progressive enlargement of the number of objects within a class of objects whose initial size = 1, singularly or as a group acting as one.
Object AREAS: PPset TRAILS
From the above, it may seem all too easy to just disregard the PPsets as simple “objects” not unlike those of any other random selection. But there is more here, than just that.
We have already seen in the BIM: Parts I-III that the PPsets are intimately related to and described by the ISL as seen on the BIM.
In Parts II & III, we saw directly how each and every PPset – set as factors on the BIM – related diagonally back to the AXIS EVEN number.
We also saw how the PPset TRAILS – that were extensively examined in Part I – are now easily seen as the PPset values occupying any Active Row on the BIM.
Now, in Part IV, we open the BIM up to see both symmetrical sides. In doing so, we see that underlining those PPset TRAILS Rows gives us the progressively larger squares: the Object AREAS of PPset TRAIL numbers.
That’s all in well, but significantly, those PPset TRAIL “objects” are not just any objects. They are a very specific collection of objects – specific PPsets that are part of specific PPset TRAILS, or groups, that ONLY exist and occupy their specific location on the BIM. A location that both allows them to individually relate back diagonally to the EVEN # on the AXIS, and, to relate ACROSS the Row as the collective set, or group, of ALL PPsets whose members consist of one constant PRIME and one PRIME Sequence PRIME, e.i., 3,11–5,11–7,11–11,11. The latter become the PPset TRAILS.
Ultimately, it is the PPset TRAILS on the Rows that interact and inform the diagonally-related EVENS. Their rate of growth – (increasing by 2 for each PS Object AREA) – far exceeds the Prime Gaps growth. This is built into the geometry of the BIM. It ensures that Euler’s Strong Form of the Goldbach Conjecture is fully satisfied!
The 1–4–9–16–25-… ISL relationship of the Object AREAS: PPset TRAILS provides a definitive and intimate connection of the PRIMES to the ISL as seen on the BIM.
~~~~*Each square AREA = sum of the ODD#s leading to it, i.e. the ODD number summation series. Thus AREA = 9 = the sum of the ODDs 1 – 3 – 5. The next AREA = 16 = the sum of the ODDs 1 – 3 – 5 – 7. The next AREA = 25 = the sum of the ODDS 1 – 3 – 5 – 7 – 9, and so on. One can calculate the tally of any given square AREA by subtracting the two previous square AREAS to get their ODDs summation value, then add 2 to that and increase the larger square AREA by its sum, e.i., 25 - 16 = 9, add 9 + 2 = ll, add 11 + 25 = 36. The next square AREA is 36 and it contains 11 PPsets in its TRAIL.
As the TRAILS follow the ISL NPS — 1—4—9—–16—25—36—49—64—81—100—…—the actual number of unique PPsets within a trail = √(square), e.i., √36 = 6. There are 6 unique PPsets: Since the TRAIL falls on Row 17, those PPsets are: 3,17—5,17—7,17—11,17—13,17—17,17.
We know Object AREA 36 = 6*6, i.e., it is the 6th in the ISL NPS. Likewise, we can take any whole √ of a number and know where it is at in the ISL NPS. Another example, √100 = 10, so on Row 31, we have 19 PPsets, with 10 of them unique: 3,31—5,31—7,31—11,31—13,31—17,31—19,31—23,31—29,31—31,31. How do we know there are 19 PPsets? The ISL NPS is, of course, based on the squares of the numbers 1,2,3,…. The difference (∆) in the AREAS being the ODD # summation series: 1+3+5+7+…difference, or simply adding 2 to the previous ODD. Adding the √ of the current and previous AREAS will give the ∆, e.i. √100 + √ 81 = 10 + 9 = 17.
So once any Row in the ISL NPS is known, we can readily determine:
1. AXIS and squared AXIS — PD — numbers;
2. The ∆ between the current ISL NPS AREA and the one previous;
3. The total number of PPsets within the current AREA;
4. The net number of unique PPsets forming the PPset TRAIL;
5. The numbers, both total and unique, of ALL other AREAS before and after.For example, Row 31:
1. AXIS = 31 and squared AXIS = 961 on AREA = 100;
2. ∆ 100 - 81 = 19;
3. PPsets total = 19;
4. Net PPsets = (19–1)/2 = 10, or simply the √100;
5. Previous AREA = 100–19 = 81, 81 –17 = 64, 64 –15 = 49, … and Next AREA = 100 + 21 = 121, 121 + 23 = 144, 144 + 25 = 169,… or simply follow the 12—22—32—42—52—62—72—82—92—102—112—122—132—…The question of how do we know Row 31 is where the ISL NPS AREA = 100 lands? Or any other PPset TRAIL Object AREA?
The rigidly regular ISL NPS — 1—4—9—16—25—36—49—64—81—100—…, — itself built on 12—22—32—42—52—62—72—82—92—102 —…, the ∆ being the ODD # summation series of 1+3+5+7+9 +11+.. with a constant ∆ of 2 — must be reconciled with the PRIMES Sequence (PS) with its variable Prime Gap.
What Row does ISL NPS AREA, say, PS 41, occupy?
We could think, well, it must be AREA 121, up 21 from AREA 100, but on what Row?
Wrong we would be, as the NEXT PS after 31 is 37, followed by 41. So Row 37 is AREA 121 and Row 41 is actually AREA 144, i.e., 102—112—122, respectively, for Rows 31—37—41.
Currently, one must know one to get the other and that one must be the PS Row. From that, one can calculate the ISL NPS AREAS and the number and configuration of ALL the PPsets within the PPset TRAIL.
If we know Row 41 — as PS 41 — we can calculate back to a known Row-AREA like Row 31—AREA 100, count the number of PS jumps from 31 to 41 — jump one to 37, jump two to 41 — and know that we have moved two positions up the ISL NPS — 100 to 121 to 144 — giving 144 as the respective AREA for Row 41.
From (122 = 144) - (112 = 121) we see there is a ∆ of 23 between the AREA 144 and the previous AREA 121.
Since we know from the PS, the previous to 41 is 37, thus AREA 121 is on Row 37. The total number of PPsets equals the AREA difference from the previous AREA, thus for 144 it is 23 and for 121 it is 21. The net unique number of 12 PPsets within the TRAIL for Row 41—AREA 144 = √144 = 12. For the Row 37—AREA 121 it equals √121 = 11.
Let’s go back to Row 41—Area 144. What lies ahead on ISL NPS AREA 441. What Row is it on? Aside from simply looking at the BIM:
• The √441 = 21.
• There are 21 unique PPsets in the PPset TRAIL.
• There are 9 jump steps from AREA 144 to AREA 441 — 144—>169—>196—>225—>256—>289—>324—>361—>400—>441, corresponding to 122—>132—>142—>152—>162—>172—>182—>192—>202—>212.
• There must be 9 corresponding jump steps for the PS: 41—>43—>47—>53—>59—>61—>67—>71—>73—>79.
• AREA 441 = Row 79
• Take 441 - 400 = 41.
• There are 41 total PPsets in the AREA 441.
• Another way to get the total 41 is to add 20 + 21.
• All the Row—AREAS between Row 41—AREA 144 and Row 79—AREA 441 are easily determined in a like manner.One more example: Starting with PS 113, what ISL NPS AREA does it occupy and what are the numbers?
• We could start from scratch with PS 3 and count the jump steps to 113 = 28.
• Now match that with 28 jump steps from ISL NPS 1 + 28 = 29.
• 292 = 841.
• There are 29 unique PPsets in the PPset TRAIL on Row 113—AREA 841.
• Take (292 = 841) - (282 = 784) = 57.
• There 57 total PPsets in the AREA 841.
• Another way to get the total 57 is to add 28 + 29.
• All the Row—AREAS between Row 3—AREA 1 and Row 113—AREA 841 are easily determined in a like manner.There are several ways to calculate the PPsets and their associated ISL-NPS AREAS. A tip to keep in mind: as the Object AREAS increase as 12,22,32,...the ∆ between them being the ODD # Summation series — 3--5--7--9... — the ∆ of the ∆, if you will, is 2. ALL total PPsets within an AREA will be ODD. Another visual way to look at this: as each AREA progressively enlarges, one new PPset is added to the Horizontal and one new PPset is added to the Vertical Row/Col, the sum equals 2, so starting with 1, 1 + 2 = 3, 3 + 2 = 5, 5 + 2 = 7,... The unique PPsets may be either.
With optimum computing power, one could determine ALL PS Row—ISL NPS AREAs up to and including the largest PRIME.
One can use the NO-PRIMES (NP) = 6yx ± y (covered extensively in PRIMES vs NO-PRIMES, 2019) to determine ALL the non-PRIMES between any run of numbers.Example: what are the NPs from 3–59?Consulting NP=6yx+-y_with3^x.jpg, you could simply pick out the NPs.Calculating the NPs:NP = 6yx ± y. Let x = 1,2,3,… and y = ODD # ≥3, and add 3 exponential, 3x:1. let x = 1, y = 32. NP = 6yx ± y = 6(3)(1)±3 = 18 ± 3 = 15, 213. let x =1, y = 54. NP = 6yx ± y = 6(5)(1)±5 = 30 ± 5 = 25, 355. let x =1, y = 76. NP = 6yx ± y = 6(7)(1)±7 = 42 ± 7 = 35, 497. let x =1, y = 98. NP = 6yx ± y = 6(9)(1)±9 = 54 ± 9 = 45, 639. let x =1, y = 1110. NP = 6yx ± y = 6(11)(1)±1 = 66 ± 11 = 55, 7711. let x =2 y = 312. NP = 6yx ± y = 6(3)(2)±3 = 36 ± 3 = 33, 3913. let x =3 y = 314. NP = 6yx ± y = 6(3)(3)±3 = 54 ± 3 = 51, 5715. add 3 exponential, 3x = 32 = 9, 33 = 2716. NPs 3—59 = 9,15,21,25,27,33,35,39,45,49,51,55, and 57.Knowing the NPs allows one to make the jumps from one known PS and its associated ISL NPS AREA to another.The value of determining the net unique number of PPsets within a TRAIL is that each TRAIL member will sequentially contribute to the pool of PPsets whose members add up to form a given EVEN. This constant and regular growth of the PPsets outpaces the rate of growth of the Prime Gaps ensuring the Goldbach Conjecture is always fulfilled.
Another valuable outcome of determining ALL the unique PPsets within ALL the encompassing AREAS is that ALL PRIMES are accounted for. Should a new and/or larger PRIME be discovered, its PS Row—ISL NPS AREA can be calculated and the net unique PPsets determined. There should NOT be any holes!
From PRIMES vs NO-PRIMES we know that we can test-validate that any ODD (≥5) is PRIME by seeing if the difference between its squared value and that of any other squared PRIME value is an even multiple of 24, e.i. 72 - 52 = 24, 312 - 112 = 840 and 840/24=35 and so on.
Note that it is the PS PRIMES from the AXIS on the BIM that is squared on the PD that follows this PRIMES validation, not the ISL NPS Object AREAS, per se, i.e., the 312 - 112 example above works as expected, but the overlaid ISL NPS Object AREAS of 100 and 16 values, respectively, do not work this way.
The latter only works when the values are from squared PS values like 121 and 49, i.e., 121 = 112 and 49 = 72, the ∆ being 121 - 49 = 72 and 72/24 = 3.
Closing remarks:
SYMMETRY, STEPS, EVENS, EVENS/2, PPsets, PRIME SEQUENCE FRACTALS, ISOSCELES & EQUILATERAL TRIANGLES, INVERSE SQUARE LAW, PYTHAGOREAN TRIPLES; ALL ON THE BIM.
In the first publication of the BIM (BBS-ISL Matrix — originally referred to as the Brooks (Base) Square—Inverse Square Law Matrix) in MathspeedST (2010), the work was divided in to two main sections:
- TAOST: The Architecture Of SpaceTime, for the simple reason that all considerations of the actual architecture of spacetime MUST revolve around the ISL as it underlies all fundamental expressions of energy — as matter and fields — dispersion.
- TCAOP: The Conspicuous Absence Of PRIMES. How can these fundamental, “atomic building blocks” of numbers actually be absent from a matrix grid that so fundamentally informs all of spacetime?
In MathspeedST, the PRIMES were found to be stealthily hidden within the BIM, revealing there presence ONLY when the BIM itself had its ODD #s 1st Parallel Diagonal modified to EVENS by the addition of 1 to each ODD.
This resulted in the original PTOP (Periodic Table Of PRIMES) on the BIM. It was refined by pulling the values off the BIM and making a separate PTOP. All this became the subject of “PTOP (Periodic Table Of PRIMES) & the Goldbach Conjecture” ebook and white paper (2019). It is also referred to as BIM: Part I. The PPsets and their TRAILS were introduced.
Not good enough just by itself, further research found that, indeed, each and every PRIME, when treated as part of a PPset, could be found and individually profiled DIRECTLY on the BIM. BIM: Part II was formed.
Still not good enough, plotting all the Lower Diagonal P2 PRIMES on a table and then re-plotting those results back onto the BIM opened up a new vista. By substituting the AXIS values for each of those P2 PRIMES from the table, one has now formed a new SubMatrix of the BIM with ALL the PPsets in place.
One immediately sees that they occupy EXACTLY the same footprint on the BIM as do the individual PRIMES (and the PPTs): namely, falling only on the BIM/24 Active Rows.
In the case of the PPsets, one can also see that this is a direct consequence of locating the PPsets as the grid space resulting from the intersection of the PRIMES Sequence (PS) of the Horizontal AXIS with the PS of the Vertical AXIS. This becomes the basis for the BIM: Part III.
In BIM: Part I-III, we have mostly used just half of the bilaterally symmetric BIM to reveal and describe the geometry.
In BIM: Part IV, we now look at the whole BIM with the PPset SubMatrix in place.
What we find is that by treating these PPsets as objects and counting them within progressively larger square areas — forming what is called “Object AREAS” — a pure ISL NPS is found. Yes, as the PS-Fractal series of each AXIS joins to form the PPsets, their actual numbers — as PPset TRAILS — progressively grows and sums up to quantities with Object AREAS that directly mirror the fundamental ISL NPS:
1—4—9—16—25–… And while this relationship of the PRIMES to the ISL can not predict the next largest PRIME, it can ABSOLUTELY account for each and every PRIME at, and below, any given PRIME, regardless of size.
While Euler’s Strong Form of the Goldbach Conjecture is proved along the way on this journey, the real significance is what we have seen unfolding in BIM: Parts I-IV. The role of Symmetry and Fractal underlie everything about the PRIMES.
The PRIMES on the BIM is all about how the fractal nature of the PS becomes expressed as symmetry on the BIM as isosceles and equilateral triangles, forming the PPsets that ultimately form ALL the EVEN numbers!
What is marvelous, incredible, mind-blowing in every way, is that this same symmetry—fractal—isosceles/equilateral triangle relationship is found — indeed, is part and parcel — throughout the BIM.
The ISL seems to reflect the most basic and fundamental relationship(s) between quantity and the numbers that account for it.
ISL—> BIM
BIM—> PPT
BIM—> PRIMES
BIM—> PPset Object AREAS
BIM—> other Object AREAS
As in showing that ALL EVENS (≥6) can be formed from the sum of two ODD PRIMES (Euler’s Strong Form of the Goldbach Conjecture), one would like to see — in the context of the PRIMES being the fundamental “atoms” — the PRIMES being the source of the ISL and everything thereafter!
PRIMES—> ISL—>BIM—>PPT & PRIMES patterns on the BIM, etc, etc.
We are not there yet.
PRIMES Index