TPISC: The Pythagorean — Inverse Square Connection, Copyright2014, Reginald Brooks. All rights reserved.

The Pythagorean - Inverse Square Law Connection (TPISC)

A MathspeedST Supplement

Reginald Brooks

brooksdesign-ps.net

First published 2014

Published by Brooks Design:535 NW 107^th Ave, Portland, OR 97229, USA

Email: inverse2ed@gmail.com

Phone: 503-646-1548

URL: http://www.brooksdesign-ps.net

All rights reserved. Without limiting the rights under copyright reserved above, no part of this publication may be reproduced, stored in or introduced into a database and retrieval system or transmitted in any form or any means (electronic, mechanical, photocopying, recording or otherwise) without the prior written permission of both the owner of copyright and the above publishers.

Permission is hereby granted for single copies to be made for personal, non-commercial use for students and teachers of schools, colleges and universities provided that: either the entire paper, including figures and tables, is kept intact; or, any extracts of the text, or figures or tables (in part or whole), be properly and visibly cited as to authorship and source.

Original illustrations/ Photographs by Reginald Brooks

ISBN [ISBN number]

Abstract

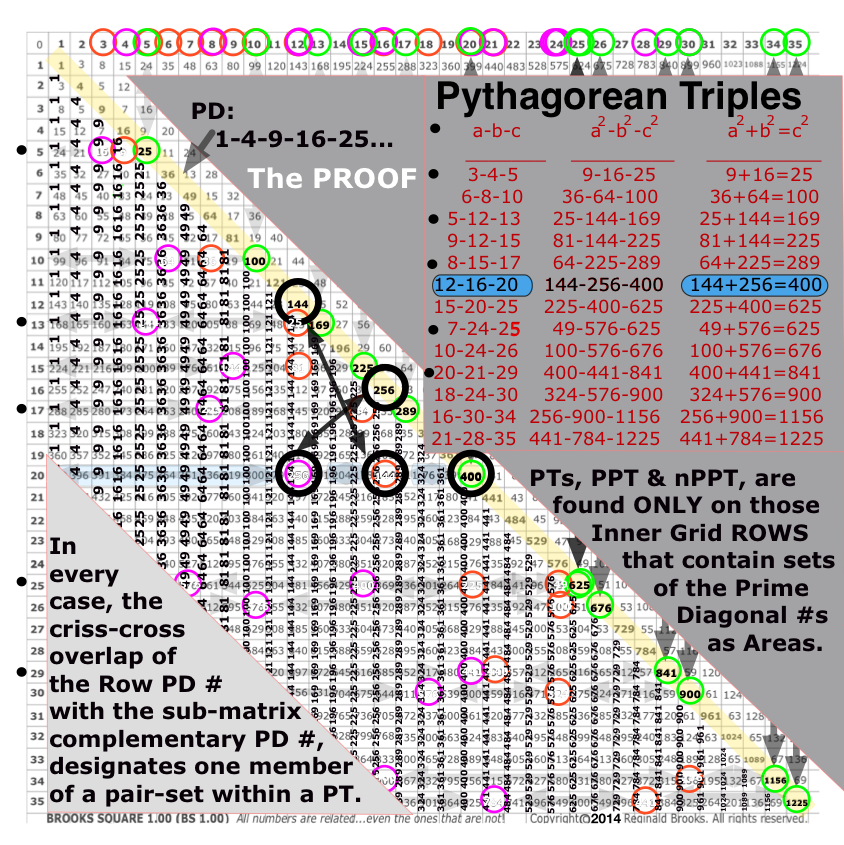
There is a simple whole number (integer) matrix grid table upon — and within — that every possible whole number Pythagorean Triangle — a.k.a. Pythagorean Triple — can be placed, and proved. The Brooks Base Square - Inverse Square Law (BBS-ISL) matrix is an infinitely expandable grid that reveals ALL Pythagorean Triples — both Primitive Triples (PPT) and their non-Primitive multiples (nPTT). An extremely simple geometric AREA proof of the Pythagorean Theorem — c²=a²+b² — is built into the BBS-ISL matrix.

Not only does the Inverse Square Law describe, define and quantify our most important energies (and their expressions as force) — gravity, light, sound, electromagnetism… — the BBS-ISL matrix grid is composed of Pythagorean Triples crisscrossing over much of the entire grid. An intimate inter-connection way beyond a simple, casual association has been revealed. The Dickson Method confirms, validates and provides insight into the generation of ALL Pythagorean Triples.

The Pythagorean Theorem and the Inverse Square Law share the same code. In this respect, the c² of c²=a²+b² equals the r² of 1/r² (ISL). Embedded within the BBS-ISL matrix — that is essentially based on the squares of whole numbers — are the Pythagorean Triples — whole number right-angle triangles of uneven legs whose area squares equal in sum that of their longer hypotenuse side. Numbers of inevitability.

The Pythagorean - Inverse Square Law Connection

(TPISC)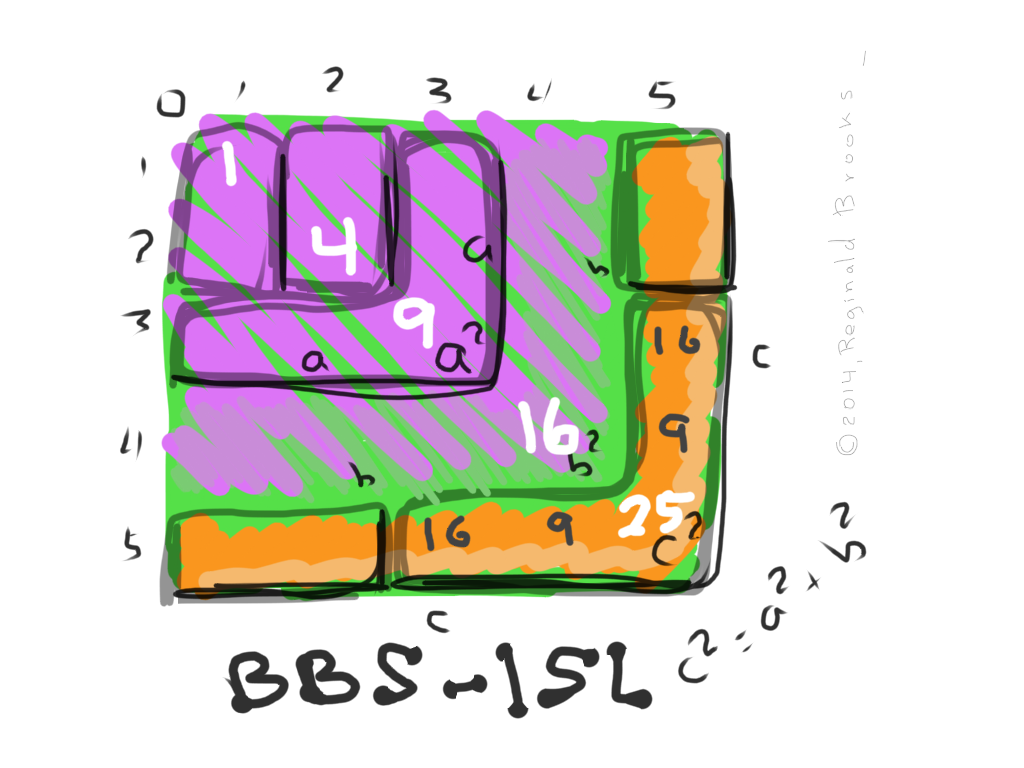

Introduction

The Pythagorean - Inverse Square Law Connection or “How the Pythagorean Theorem is intimately embedded within the The Architecture Of SpaceTime (TAOST) as described by the BBS-ISL matrix” is first and foremost the topic of this paper. It is a MathspeedST Supplement.

As one of the most influential mathematical descriptions of all time, there is no shortage of writings, descriptions and/or proofs of this most profound theorem.

The reason that this paper is being presented is precisely because the very nature of that geometric relationship of the Pythagorean Triangle — whereby the area of the square of the long side (hypotenuse) is equal to the sum of the squares of the two shorter sides (legs) — is so intimately related to the Inverse Square Law (ISL), as depicted in the BBS-ISL matrix (Brooks Base Square - Inverse Square Law matrix), that a cause and effect relationship between the two is unavoidable.

That the BBS-ISL matrix also provides perhaps the simplest, most intuitively obvious proof to the Theorem directly on the grid only supports the argument. Every possible Pythagorean Triple (PT), and its proof, is visually and mathematical present. The Dickson Method confirms this.

The Pythagorean - Inverse Square Law Connection will often be referenced as TPISC.

A NEW short INTRO has been added!

Brief History

BBS-ISL Matrix

The brief history of the development of the BBS-ISL matrix is summarily listed below. For the full treatment, please go to

http://www.brooksdesign-ps.net/Reginald_Brooks/Code/Html/arthry5.htm where the individual papers are presented. You can find individual links to the key papers in Appendix A of this paper.

1985: L.U.F.E. (The Layman’s Unified Field Exposé) was published. The first seeds of the BBS-ISL planted.

1987: GoMAS (The Geometry of Music, Art and Structure, first edition) was published. The ISL informs it all!

2001-06: PIN (Pattern In Number) various papers on geometric number patterns, primes and the axial structure of DNA — ISL

2003-08: various papers on Quantum and Gravitational physics, including The Conservation of SpaceTime

2009: GoMAS, Part I — ISL

2012: GoMAC, Part II & III — ISL

2009-12: Brooks (Base) Square and The Inverse Square Law published — 200 BASIC BBS-ISL “Rules” on TAOST (The Architecture Of SpaceTime) and TCAOP (The Complete Absence Of Primes)

2011-13: Brooks (Base) Square Interactive Matrix — hands on ISL

2011: TAOST (The Architecture Of SpaceTime) — ISL

2012: Numbers of Inevitability — ISL

2013: AFPOP (A Fresh Piece Of Pi(e) and the √2, too…Fractal-Fractal-Fractal) — more Archimedean Geometry to backup the ISL

2012-13: LightspeedST (Why is the speed of light constant?), a series of 8 papers, hundreds of images and 50 short videos ultimately recast into an interactive ebook published in the iBookstore. LightspeedST forms the complementary work to MathspeedST.

2013-14: MathspeedST (How can information be ubiquitous, effectively traveling FASTER than the speed of light?). This freely available interactive ebook brings together under one publication the Brooks (Base) Square-Inverse Square Law, or BBS-ISL matrix for short, under the title MathspeedST. It includes hundreds of images, a number of videos and lots of test-yourself, interactive widgets in presenting the derivation, layout, rules, patterns and ISL-derived mathematical basis of the matrix. Available for free in the iBookstore

The BBS-ISL matrix has shown remarkable inter-connections to all forms of geometry and number theory including a section on the distribution of the non-Primitive Pythagorean Triples. The Architecture Of SpaceTime as defined by the BBS matrix and the ISL is certainly one of boldest and far-reaching claims. The TCAOP (The Complete Absence Of Primes) brought out the Periodic Table of Primes (PTOP) is a hidden gem. And now, we have every possible PT — PPT and nPPT — presenting itself and its proof on the BBS-ISL matrix.

Pythagorean Theorem

The history, derivation, use and the hundreds of proofs of the Pythagorean Theorem would fill a library all onto itself. Classic proofs from Pythagoras, Euclid, da Vinci, Newton, Bhaskara, Einstein, Garfield, and the list goes on, are well documented — many with beautiful and clever animations. These proofs generally rely on rearrangement, similarity, or division of the triangle to reveal the equality of the areas formed. Algebraic and other forms of abstract mathematics can also do the trick.

Although there are a large number of references cited, here are three that will bring you up to speed as to terminology, proofs and their history:

1 .http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Pythag/pythag.html

2. http://www.cut-the-knot.org/pythagoras/index.shtml

3. http://en.wikipedia.org/wiki/Pythagorean_theorem

The Pythagorean Triangle (PT) is right-angle triangle composed of whole number (integer) sides. The two shorter sides or legs, a and b, are of differing lengths, as is the longer or hypotenuse side. Note that other right-angle triangles with fractional sides follow the Pythagorean Theorem — but are not Pythagorean Triangles.

The PTs can be divided into two groups: Primitives and non-Primitives. The Primitive PT (PPT) is one that is irreducible. The non-Primitive (nPPT) is simply a multiple of a Primitive, e.i. a 6-8-10 nPPT is simply a double of the 3-4-5 PPT.

The pervasive distribution of all the possible PTs (PPT and nPPT) is amazing — going to infinity. Quoting Professor Knott in the first reference above: ”Can any number be a side in some Pythagorean Triangle? is Yes!”

TPISC

Introduction

Brooks Base Square (BBS) is a matrix grid of the Inverse Square Law (ISL), referred to as simply the BBS-ISL matrix. Every number — integer — value on the matrix grid is made from the Prime Diagonal (PD). The PD is made from the squares of the Axial numbers (0), 1,2,3,… It divides the matrix into two symmetrical halves — the lower of which gets our attention solely for convenience of display.

The Inner Grid simply refers to that part of the matrix between the Axis and PD. It contains no even numbers not divisible by four. Take away the first Parallel Diagonal to the PD (3,5,7,…) and the Inner Grid — now referred to as the Strict Inner Grid — also does not contain any prime numbers. All other numbers are present.

Between the PD, Axis and Inner Grid, the BBS-ISL matrix can reveal remarkable, amazing, even mind-blowing interconnected patterns — many that have peen presented in the BASICS of MathspeedST.

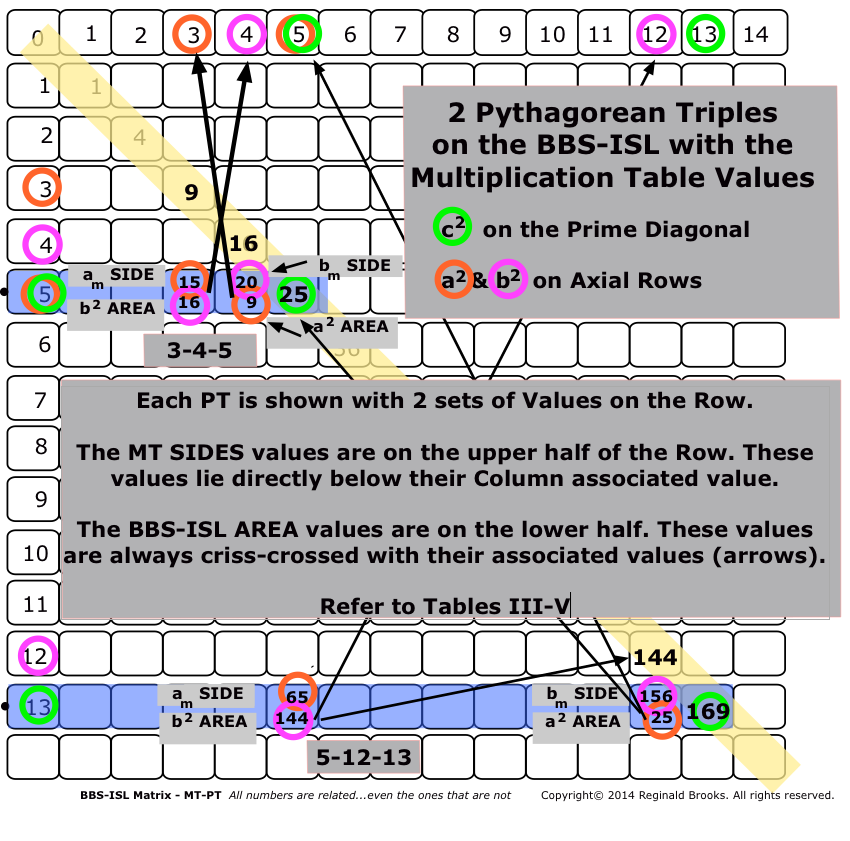
Included in those first 200 “Rules,” Rules 81-86 reveal that over 50% (or more) of the entire matrix grid — a grid that is infinitely expandable — consists of the many multiples of the Pythagorean Triple (PT) triangle 3-4-5. The multiples, or siblings, of the Primitive are simply 2x, 3x, 4x, … that of the parent. The 12-16-20 is the smallest PT to fit on the grid diagonally. All such multiples — and there are generations of them — line up their SIDE values (i.e. Legs and hypotenuse) along a given Diagonal, parallel or perpendicular, to the PD. These are their “SIDE” values as opposed to the the “AREA” values formed from the SIDES values.

New in the MathspeedST Supplement are the PT “AREA” values of every possible Primitive (PPT) or non-Primitive (nPPT) triangle laid out on the matrix with c² at the PD and a² and b² on the ROW leading to it!

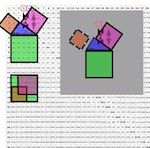
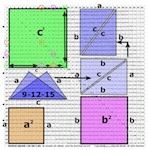
TPISC icon

Before delving into the specifics, the major takeaway on TPISC can be found right in the icon/logo used to identify the MathspeedST Supplement.

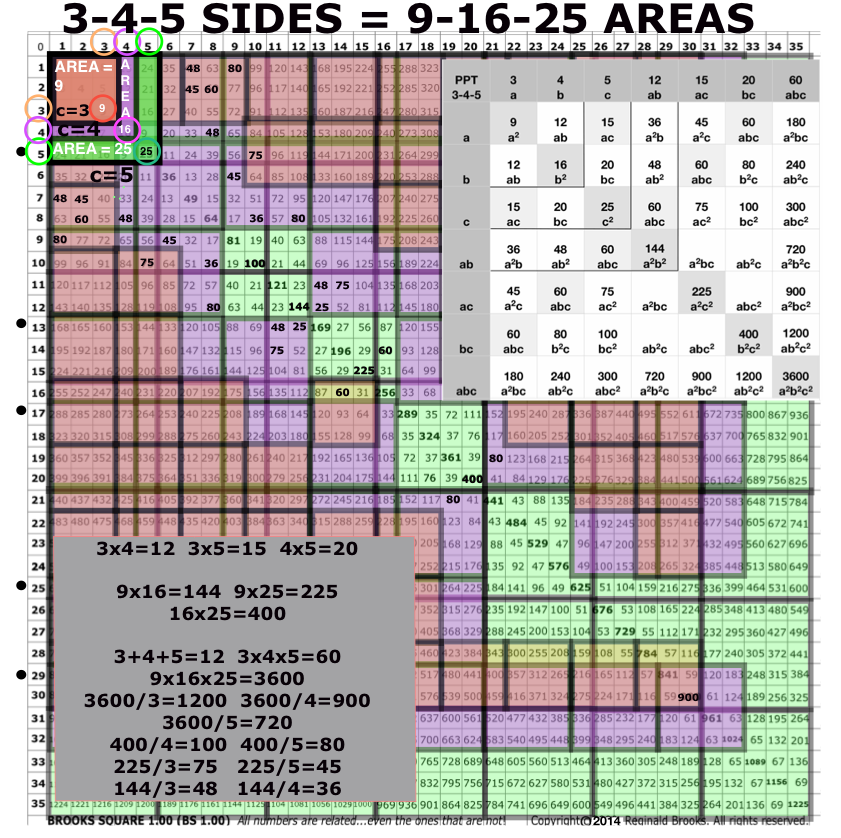
Within this simplified 5x5 BBS-ISL matrix grid we have the Prime Diagonal (PD) down the center. The square Areas are marked 1,4,9,16 and 25.

The first PPT has Sides 3-4-5 as a-b-c and their Sides squared (Areas) as a²-b²-c² or 9-16-25. The latter show up in two places on the grid.

First, in the actual PD Square Areas, we can see 3²=9—4²=16—5²=25.

Notice that the Areas are stacked on top of each other like layers. Each Area starts at 0. Also notice that the 9 little squares of Area 3²=9 (a²), when added to the 16 little squares of Area 4²=16 (b²), the resulting sum is 25 little squares of Area 5²=25 (c²), or the Pythagorean Theorem of a²=b²=c². C²=a²=b² is visually proved right on the BBS-ISL matrix.

Secondly, the same AREA information shows up directly on Axis Row 5. Remember, 5 is c=hypotenuse and c²=25 is found along Axis Row 5 at the PD. The a²=3²=9 and b²=4²=16 AREAS are found on the same Axis Row 5.

This scenario is true for ALL PTs and they — and their proofs — are ALL found on the BBS-ISL matrix.

Finally, you might ask, just what determines the actual placement — what determines the actual Primitive Pythagorean Triangle (PPT) and subsequently what rows do these primordial triangles occupy? What comes first, the location or the identity, or are they established as one? The children-sibling non-Primitive Pythagorean Triangle (nPPT) multiples are simply that — 2x, 3x, 4x, …of their parent Primitives. But what determines PPT values? This big, big question is addressed (no pun!) toward the end of the paper, but here is a hint:

If all quantities are enumerated by some counting scheme — whether it is counting on your fingers (BASE_10), your computer (BASE_2), or something else or between (BASE_3,_4,_5_6_8) — if a pattern emerges consistently between all such BASES and the quantities that they represent, surely this represents some deeper connection — an interconnection — between the two, the describer and the described. The PPT seems to have this connection with the ISL as laid out in the BBS-ISL matrix.

Also, another “locator” pattern is this: If you take the difference (∆) between the c=hypotenuse values of every PPT, it is ALWAYS a ∆ of a multiple of 4, i.e. 1x=4, 2x=8, 3x=12, 4x=16,…where x=4. This is NOT true for the sibling nPPT multiples!

For some, reading this paper in reverse order — back to front — would provide the greatest benefit as it reveals the larger view first and thus gives a context for that that comes before.

Reading in the traditional order will be addressed by the outline shown below. Feel free to jump ahead, back and forth — especially with the large number of visuals — to generate this larger view as you go.

Outline for this section:

A. Classic Proofs of the Pythagorean Theorem on the BBS-ISL matrix

B. New Proofs of the Pythagorean Theorem on the BBS-ISL matrix

C. Pythagorean Triples on the BBS-ISL matrix

1. Primitives (PTT) — “parents”

2. Non-Primitives (nPPT) — “sibling” multiples

3. Distribution

a. SIDES

b. AREAS

C. SIDES In Place of AREAS

In the Inter-connection section that follows:

A. BASE_2_3_4_5_6_8_10 PT

B. BASE_3

C. BASE_4

D. BASE_5

E. Circle-Pentagon Displays

A. Classic Proofs on the BBS-ISL matrix

The Pythagorean Theorem describes any right-angle triangle with side “c” (hypotenuse) > side “b” > side “a” such that the Area formed from side c= the sum of the Areas of side a and side b — as c²=a²+b².

While there are somewhere near 1000 proofs, only those right-angle triangles composed solely of whole numbers (integers) will be considered here. Integer Pythagorean triangles are called Pythagorean Triples/Triads (PT).

The PTs can be further divided into Primitive (PPT) and non-Primitive (nPPT) categories. The PPTs, or parent PT, are irreducible, while the nPPTs, or child-sibling PT, are simply 2x, 3x, 4x.. Multiples of the unique parent PT.

Since all presentations and proofs of the PTs will be upon the BBS-ISL matrix, the following format will be utilized:

Zero (0) is top left
Prime Diagonal (PD) runs from zero to bottom right
BBS-ISL is symmetrical about the PD
Typically, only the lower half is used
Rows refer to Horizontal Rows from the left Axis
Columns refer to Vertical Columns from the top Axis
Diagonals may be Parallel or Perpendicular to the PD
The BBS-ISL is NOT a multiplication table, even though the PD=Axial numbers squared
The BBS-ISL is NOT a ruler, but a matrix grid of interrelated numbers all based on the ISL and derived from the PD
SIDES of PT triangles, and the Sides of AREAS of the SQUARES they form concern us here
These SIDES and AREAS may be diagrammatically shown to scale (or not) anywhere on the matrix for visualization but are only truly QUANTITATIVE when specifically located as values:
- 1. The PT SIDES (a-b-c) exist along the matrix Diagonals
- 2. The PT AREAS (a²-b²-c2) exist on a Single Horizontal Row
- 3. Three PT SIDES and AREAS come together starting at the Zero (0) point of the matrix — overlapping as each starts at Zero (0).
- 4. All PTs — PPT and nPPT — can and do exist within the BBS-ISL matrix in ALL three forms listed above
- 5. Not all Rows contain PTs, yet some Rows contain two or more PTs

This paper presents both translation and invention-discovery. The simple beauty of the Classic Proofs of the Pythagorean Theorem are translated onto the BBS-ISL matrix where it has been discovered that these very same PTs have a nearly ubiquitous presence. Indeed, their very simple proofs are simplified even further!

~Pythagorean Proof Sequence~

Image Reference 1

Webpage: Animated Gif, Slideshows, Movies and Images

~Pythagorean Proofs Classic~

Image Reference 2

Webpage: Animated Gif, Slideshows, Movies and Images

B. New Proofs on the BBS-ISL matrix

~New Proofs −1~

Image Reference 3

Webpage: Animated Gif, Slideshows, Movies and Images

~New Proofs −2~

Image Reference 4

Webpage: Animated Gif, Slideshows, Movies and Images

~New Proofs −3~

Image Reference 5

Webpage: Animated Gif, Slideshows, Movies and Images

~New Proofs −4~

Image Reference 6

Webpage: Animated Gif, Slideshows, Movies and Images

~Classic & New Proofs Examples 1-10~

Image Reference 7

Webpage: Animated Gif, Slideshows, Movies and Images

C. Triples Proofs and Distribution on the BBS-ISL matrix

~Triples Proofs~

Image Reference 8

Webpage: Animated Gif, Slideshows, Movies and Images

1. Primitives

Basically, Primitives are the unique Pythagorean Triples that are irreducible — they cannot be factored any smaller. They are the parents.

The Primitive Pythagorean Triple (PPT) occupies a unique geometric form. Like the Primes, it represents that which is a fundamental entity that defies any other form of distillation. It is the pure form of the PT.

As will be seen, there are several numeric patterns on the BBS-ISL matrix that suggest ALL potential PTs can be predicted and found.

Numerous references have shown enormous efforts in the listings of algebraic solutions to revealing ALL possible PTs. TPSIC is a unique demonstration of how All possible PTs can be found, proved and predicted within the BBS-ISL matrix.

2. non-Primitives

Basically, non-Primitives are the multiple copies of the parent Primitive Pythagorean Triples — they are reducible — they can be infinitely reproduced as 2x, 3x, 4x, … their Primitive source. They are the children-siblings and they are nearly ubiquitous.

So, if the Primitive PTs are so fundamentally pure, what does that say of the masses — the redundant, reiterative, self-similar copies — the fractal-like non-Primitive Pythagorean Triples (nPPT)?

Both the PPTs and nPPTs have an infinite number of possible forms, the nPPT far, far out-number the PPT simply because they are multiples of the parent form.

3. Distribution

The distribution of the PTs is perhaps the most interesting aspect of their existence. Once we understand how they are all over the BBS-ISL matrix, the real question becomes how do these SIDES and AREAS of the Squares formed become distributed over the grid. Since ALL possible PTs and their proofs exist on the matrix — though not on every Row, Column or Diagonal — what are the patterns of SIDES and AREAS telling us about:

The actual formation of the PPT?
The nature of the BBS-ISL matrix itself?

The BBS-ISL Matrix:

The PD is made of the squares of the Axis numbers;
Every number within the Inner Grid comes from a difference in 2 PD numbers;
The Inner Grid contains NO even numbers not divisible by 4;
The Strict Inner Grid — the Inner Grid minus the 1^st Parallel Diagonal — contains NO Prime numbers;
Every Row (past 3) contains alternating odd and even numbers;
The PD also contains alternating odd and even numbers;
Whenever a Row contains a PD number, it always contains a second PD number as they always occur in pair-sets of two;
A Row can contain more than one pair-set of PD numbers;
A pattern of Rows containing PD numbers is revealed when comparing the BBS-ISL matrix in various BASEs_;
A standard multiplication table overlaid upon the BBS-ISL matrix reveals a deceptively similar distribution of the Pythagorean pattern.

Formation of the Pythagorean Triples as revealed in the BBS-ISL matrix:

The SIDES (values) of both PPT and nPPT are present in parallel and perpendicular Diagonals;
The AREAS (values) of both PPT and nPPT are present on select horizontal Axial Rows;
The AREAS are the Square AREAS of the SIDE values;
These AREAS occur as complete sets — one for each PT — with the two legs or SIDES (a,b) as a pair-set contained in the Row, culminating with the hypotenuse SIDE (c) on the PD;
There are NO partial, incomplete PT sets on other Rows;
A Row may contain more than one PT set;
The difference (∆) between the c=hypotenuse values of every PPT is ALWAYS that of a multiple of 4, as 4,8,12,….;
This is NOT true for the nPPTs.

As one can see, there is a hugh overlap between the Formation of the PTs and the BBS-ISL matrix. In addition, when a standard Multiplication Table is overlaid upon the BBS-ISL matrix, in the IDENTICAL cells on the grid, an identical PT pattern is found but with a difference. That difference is that on the BBS-ISL matrix the PTs found on the Axial Rows are ALL made up of the AREAS while on the standard Multiplication Table these same PT slots are made up of SIDEs. More on this will follow further down in this section. Right now, focus will be on TPISC — The Pythagorean Inverse Square Connection.

Table I. Differences (∆) in the hypotenuse values (“c”) in PRIMITIVE PTs.

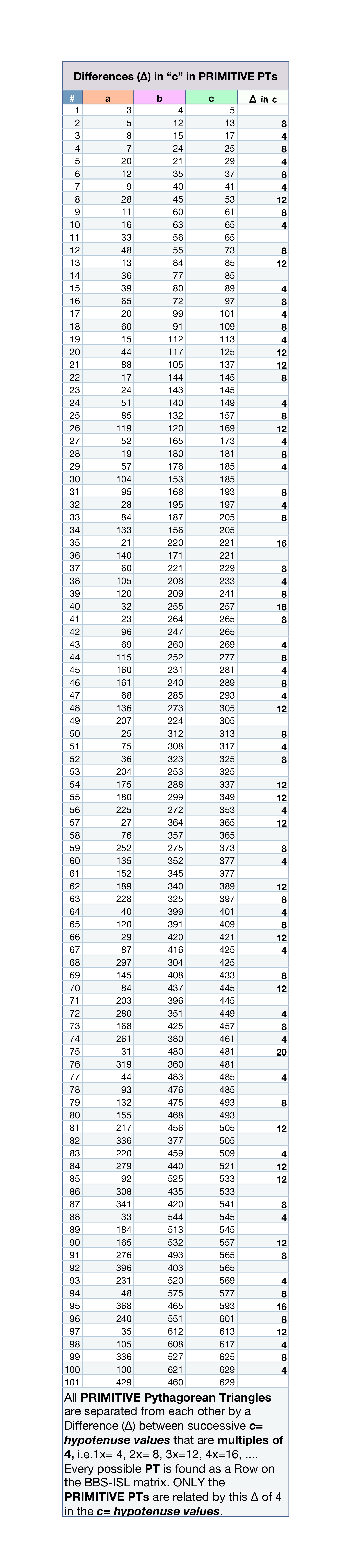Click HERE for a PNG version.

Table II. All Pythagorean Triples from hypotenuse “c” = 5 to 1225. Non-Primitives have their Primitive source shown in parenthesis.Click here to go to original source. Click here for a PDF version, or HERE for a GIF version or HERE for a PNG version.

a. SIDES

SIDES are simply the integer values for the sides (two legs, a and b, + the hypotenuse, c). The PTs are designated by their sides, a-b-c.

SIDES appear within the BBS-ISL as multiple generations, all either parallel or perpendicular to the Prime Diagonal, PD.

The nPPT SIDES have been showcased extensively in Rules 81-86 of the original Brooks (Base) Square and The Inverse Square Law (ISL) work that was to become MathspeedST. Now, one can see that the Primitive SIDES are ALSO displayed Diagonally.

Rule 81

Rule 83

b. AREAS

AREAS are simply the integer values for the squares of the sides (two legs, a and b, + the hypotenuse, c). The PTs are designated by their sides, a-b-c, but a great deal of new information is revealed in studying their AREAS.

AREAS appear within the BBS-ISL as complete AREA sets — a pair-set of the two leg AREAS + the hypotenuse AREA — the former along the Axial Row and culminating in the latter at the PD.

Neither the PPT or the nPPT AREAS have been showcased in the original Brooks (Base) Square and The Inverse Square Law (ISL) work that was to become MathspeedST. This is new, creative-discovery work revealed here for the first time.

The real value in working with the AREAS of the PTs, both individually as PPT or nPPT, and together, is that one gets an absolutely unique, visual look at how both of these PTs are embedded within the BBS-ISL matrix.

As was discovered only very recently, a new and very interesting pattern has emerged when the BBS-ISL matrix is overlaid with a matching standard Multiplication Table. In the identical cells of both grids, the same PTs emerge, only now in the Multiplication Table, it is the SIDEs — well, sort of, as you will see — that are now in the place of the AREAS on the BBS-ISL matrix! This is an important section with some very new information!

c. SIDES In Place of AREAS

On the BBS-ISL matrix:

AREAS appear within the BBS-ISL as complete AREA sets — a pair-set of the two leg AREAS + the hypotenuse AREA — the former along the Axial Row and culminating in the latter at the PD.

On the standard Multiplication Table:

A new and very interesting pattern has emerged when the BBS-ISL matrix is overlaid with a matching standard Multiplication Table. In the identical cells of both grids, the SAME PTs emerge, only now in the Multiplication Table, it is the SIDEs — well, sort of, as you will see — that are now in the place of the AREAS on the BBS-ISL matrix!

SIDES are simply the integer values for the sides (two legs, “a” and “b,” + the hypotenuse, “c”). The PTs are designated by their sides, a-b-c.

SIDES appear within the BBS-ISL along Diagonals as multiple generations, all either parallel or perpendicular to the Prime Diagonal, PD.

SIDES in the Multiplication Table appear in the Axial Rows of the table.

Their location is identical to that of the AREAS for the same PT on the BBS-ISL matrix, only the cell values designate SIDE values — NOT AREA values. The location is the same. Please take your time as this becomes sorted out.

The distribution is the same, the PTs are true PTs, yet all the numbers for the two “legs” are different — the PD numbers for the hypotenuse are the same numbers, but with different meanings.

For one, the table is a Multiplication Table. Each cell is a product of its two Axial numbers. BBS-ISL is NOT a multiplication table.

For two, the actual SIDE number values are different: the 3-4-5 PPT located on Row 5 shows 15-20-25, or 5x the SIDE values.

For three, every PT — PPT and nPPT — is a product of the original PT SIDEs values x it Row number.

Naturally, this means that All these PTs are now multiples and thus non-Primitives.

Every conventional PT found on the BBS-ISL matrix is now — in the exact SAME location — transformed from AREAS to SIDES, and, raised in value by the Row number x the original SIDES value.

Surely, this points to yet another deep connection between the Primitives and their multiple offspring, the non-Primitives in a way that is much more than the latter simply being whole number duplicates of the former. Or does it? Actually, what it shows is the deeper connection between the BBS-ISL and a standard Multiplication Table — more than any new connection to the PTs.

The Multiplication Table can be transformed into the BBS-ISL matrix by:

1. Adding the two Axis numbers that make up that cell, e.i. 15 = 3x5, so 3+5=8;

2. Multiplying that sum by the BBS-ISL sub-matrix 1 cell value, e.i. 2, so 2x8=16 (16 is the cell value on the BBS-ISL).

3. The PD values on BOTH are identical in numerical value and this is the key.

The entire BBS-ISL matrix grid is formed from the PD values. Ultimately, the same is true for the Multiplication Table. The Multiplication Table is less restrictive upfront because it does contain ALL whole integer numbers within its “Inner Grid” borders — including even numbers not divisible by 4 — and, like the BBS-ISL, outside of the single (x1 for the MT and the 1^st Diagonal for the BBS-ISL) it also contains NO PRIMES. Set this part aside.

It may be helpful to look at the connection between the Multiplication Table, BBS-ISL and the PTs by plotting all three on a reduced BBS-ISL matrix and utilize this to reference the Table that follows.

Image Reference 9

Webpage: Animated Gif, Slideshows, Movies and Images

(These 5 links all go to the same webpage)

Image Reference 9

Webpage: Animated Gif, Slideshows, Movies and Images

(These 5 links all go to the same webpage)

Image Reference 9

Webpage: Animated Gif, Slideshows, Movies and Images

(These 5 links all go to the same webpage)

Image Reference 9

Webpage: Animated Gif, Slideshows, Movies and Images

(These 5 links all go to the same webpage)

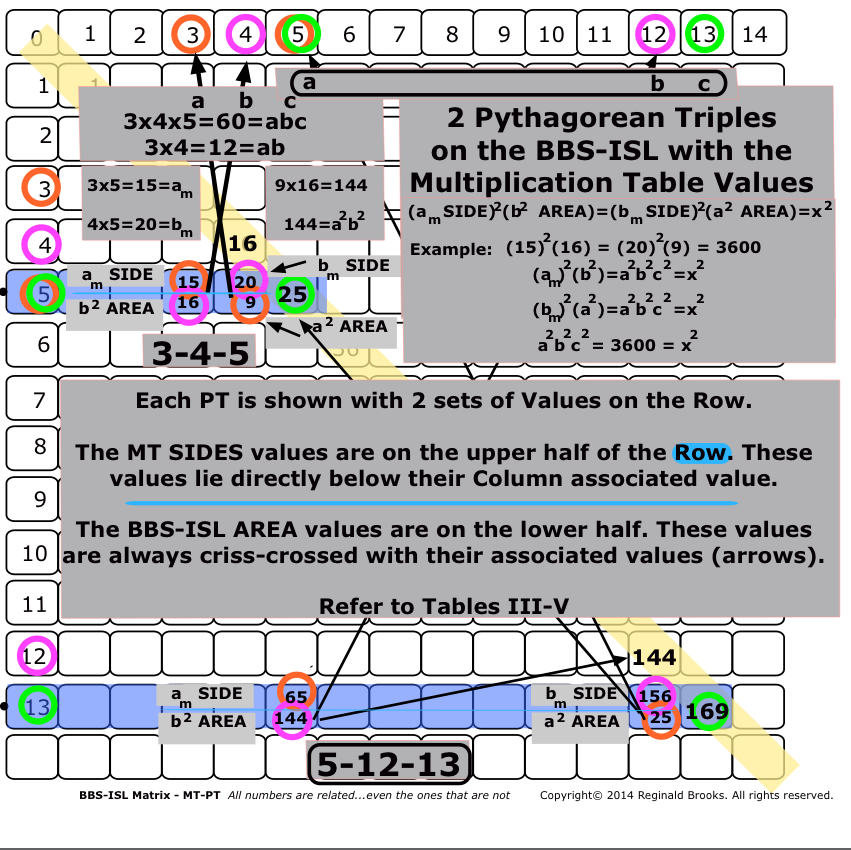
In Tables III-V below, the inter-connections between the standard Multiplication Table presentation of the PTs and that on the BBS-ISL matrix have been charted. Initially, it seemed — and rather confusingly so — that the product of the SIDES of the MT x the AREAS of the BBS-ISL was merely pointing at that deeper connection of the MT to the BBS-ISL. And yet, it looks from the view of Table III that the initial 3-4-5 Primitive PT is actually forming all other PTs, including all other Primitives.

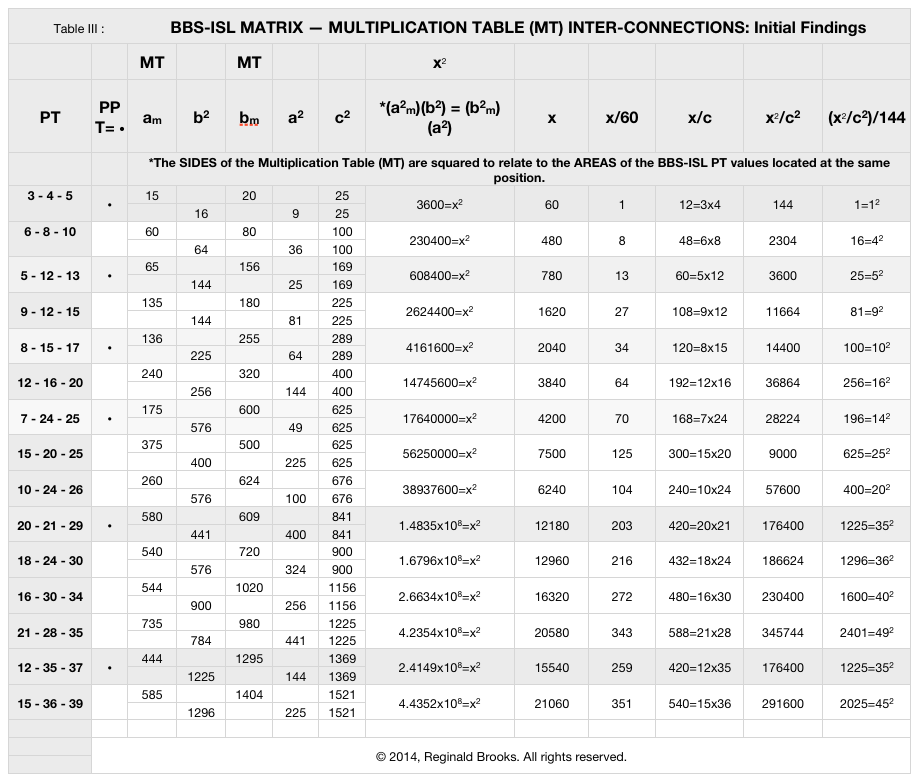
Upon further examination, a clearer view was found. The translations of the column headers in Table IV below show the process.

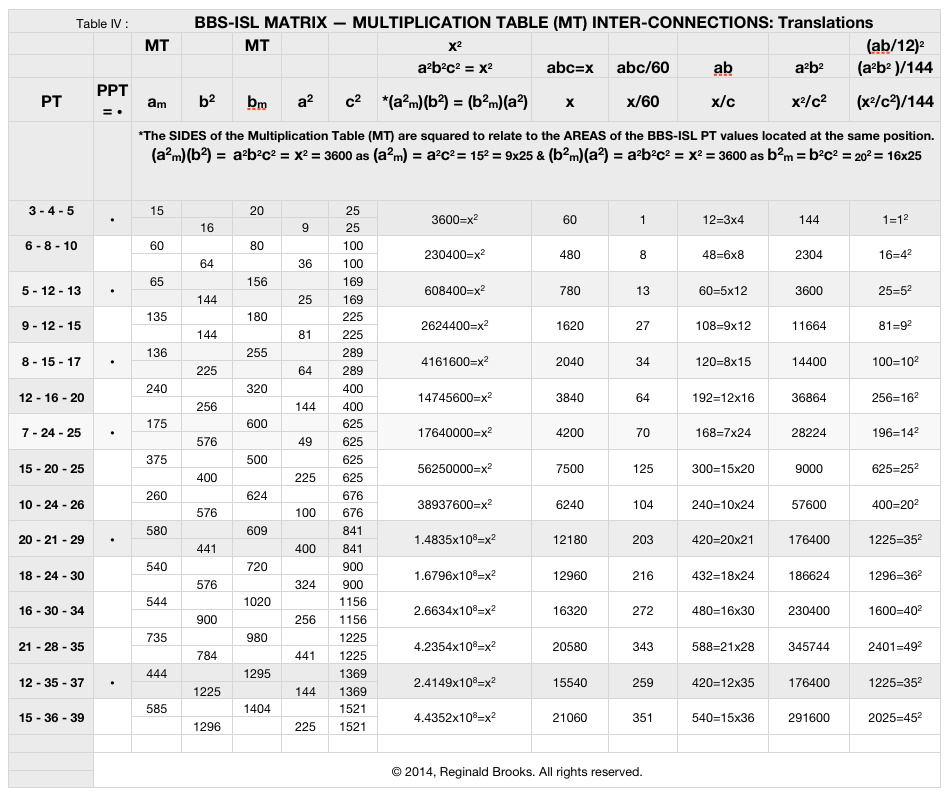
The final simplification of the BBS-ISL Matrix — Multiplication Table (MT) Inter-connections is shown in Table V below.

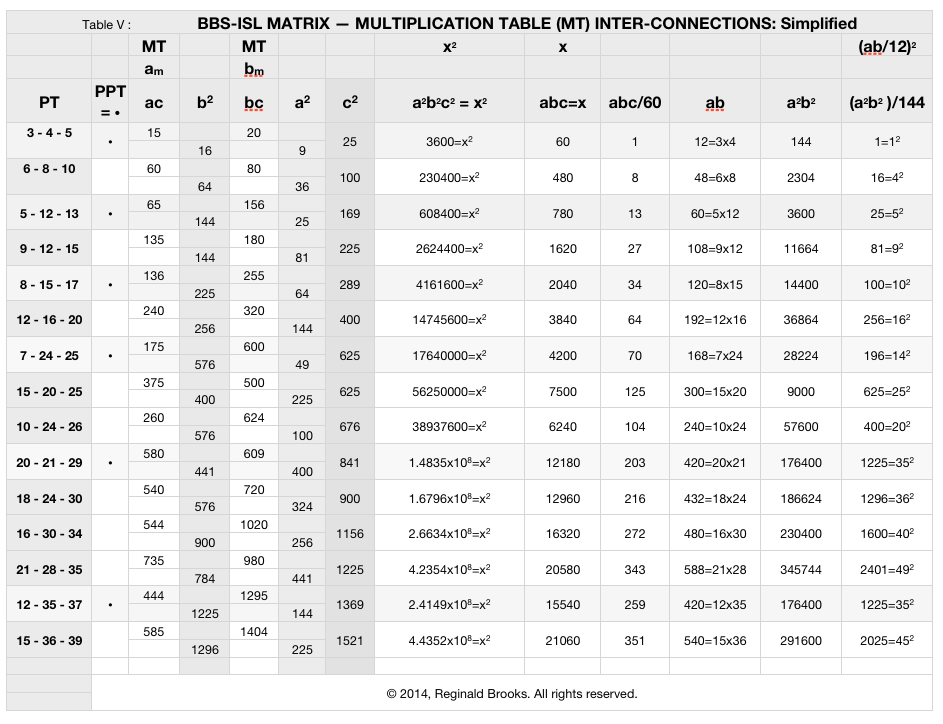
The emphasis now is back onto the BBS-ISL matrix. The related parameters are expressed simply in terms of a-b-c (or “x” when combined).

Clearly, the 3-4-5 Primitive Pythagorean Triangle is the fundamental PT for ALL PTs — Primitive and non-Primitives alike. Every PT is relatable back to the 3-4-5 PPT by a factor of 60 (abc), 144 (a²b²) or 12 (ab), the √ of the latter.

It turns out that those confusing MT values of what was thought to be the SIDES of PTs located at the exact same cell position, and previously referred to in the diagrams and charts above as a_m and b_m, are really the product of the SIDES ac and bc, respectively.

The easiest and most informative way to see the intimate inter-connections between the a-b-c’s of ANY PT is to plot them out following the template shown below in Table VIa.

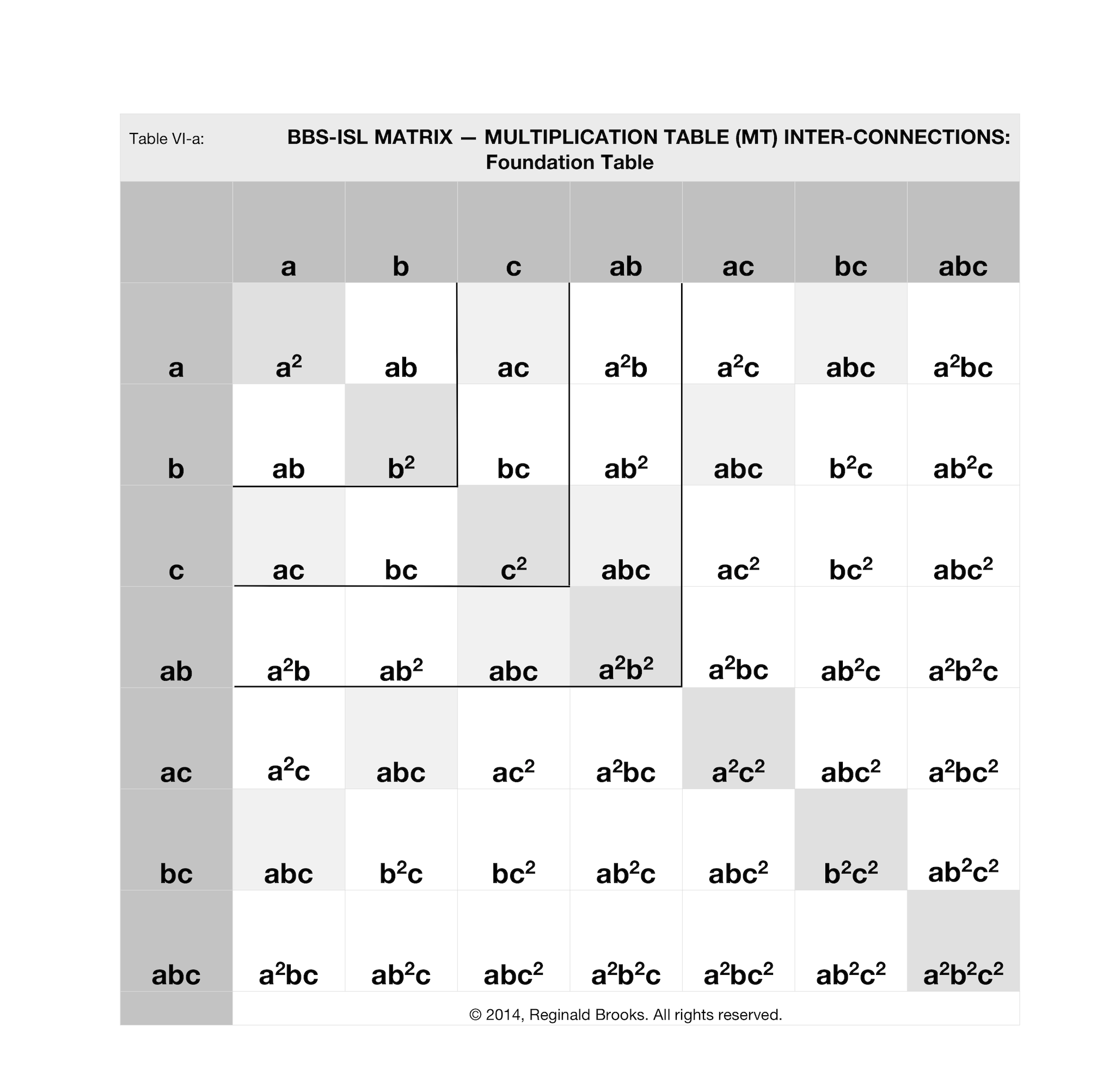
Notice that, like a simple multiplication table grid, the simple combinations of a-b-c are plotted on each axis. The key products have been given some light shading emphasis within the grid.

Below, in Tables VI-X, four PPTs and one nPPT have been laid out on the “Foundation Table.” All PTs can be done exactly the same way following the values given in Table V above.

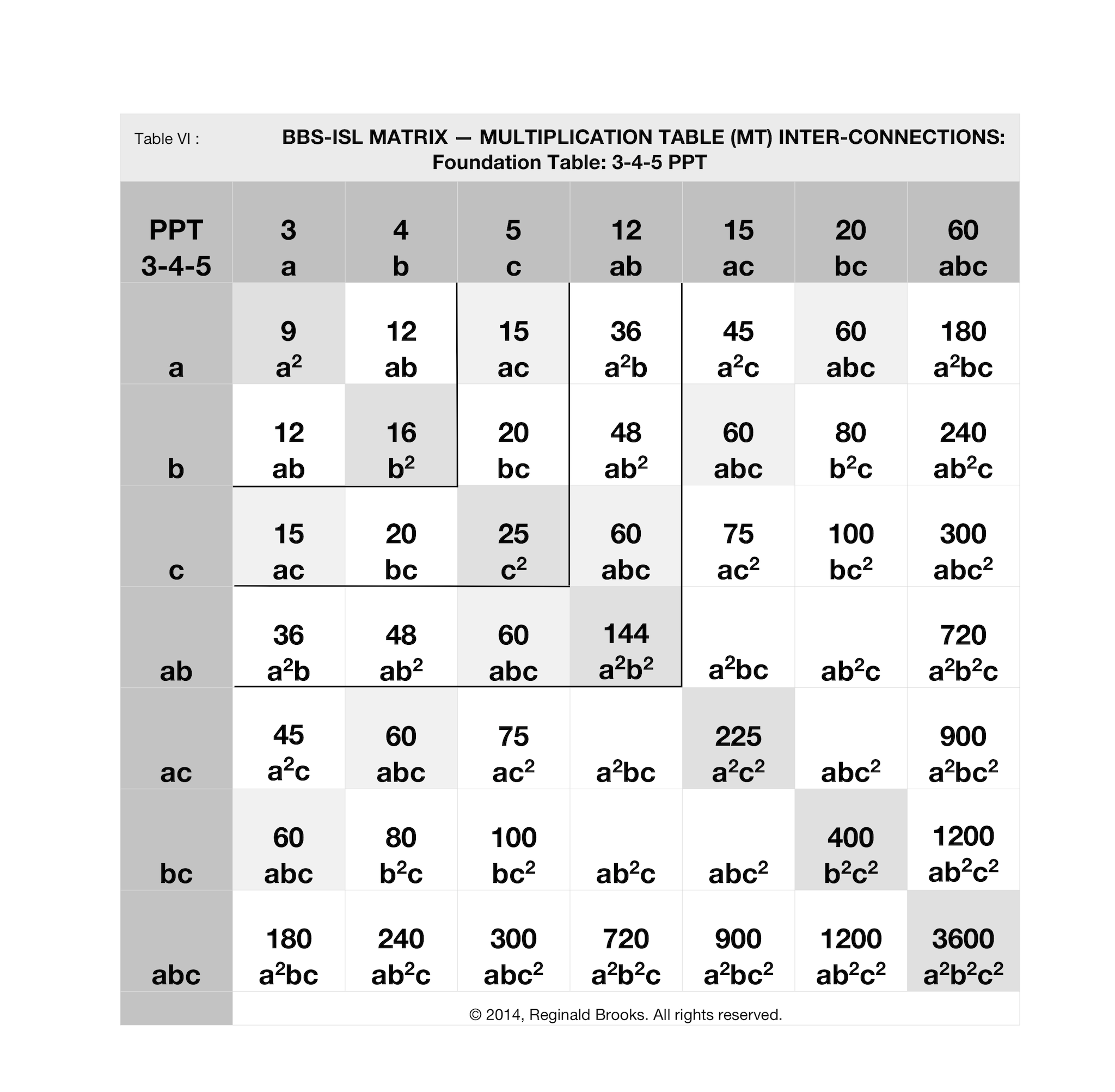
In the 3-4-5 PPT above in Table VI, the key cell values are:

a²=9
b²=16
c²=25
ab=12
ac=15
bc=20
abc=60
a²b²=144
a²c²=225
b²c²=400
a²b²c²=3600

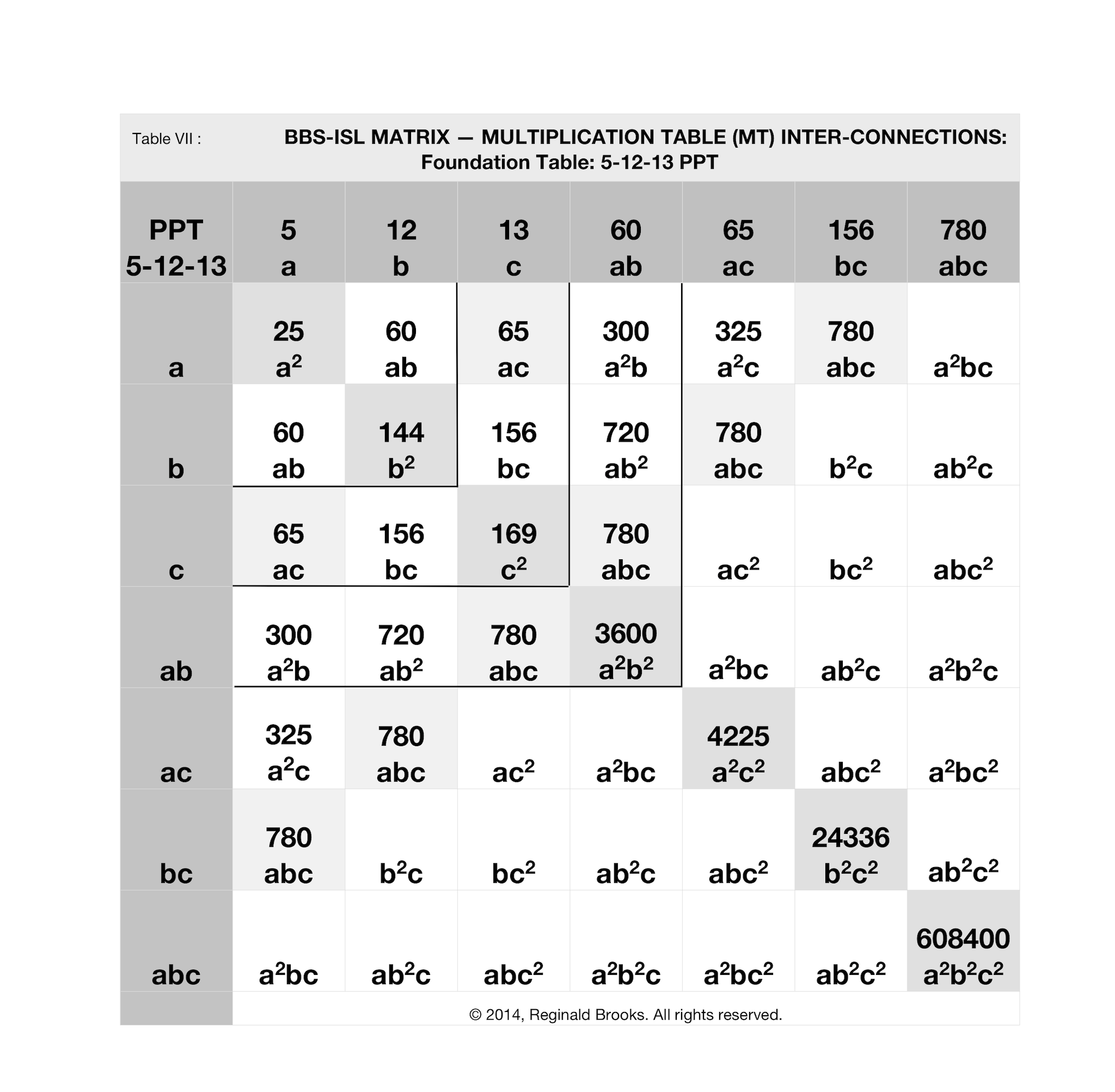
In the 5-12-13 PPT above in Table VII, the key cell values are:

a²=25
b²=144
c²=169
ab=60
ac=65
bc=156
abc=780
a²b²=3600
a²c²=4225
b²c²=24336
a²b²c²=608400

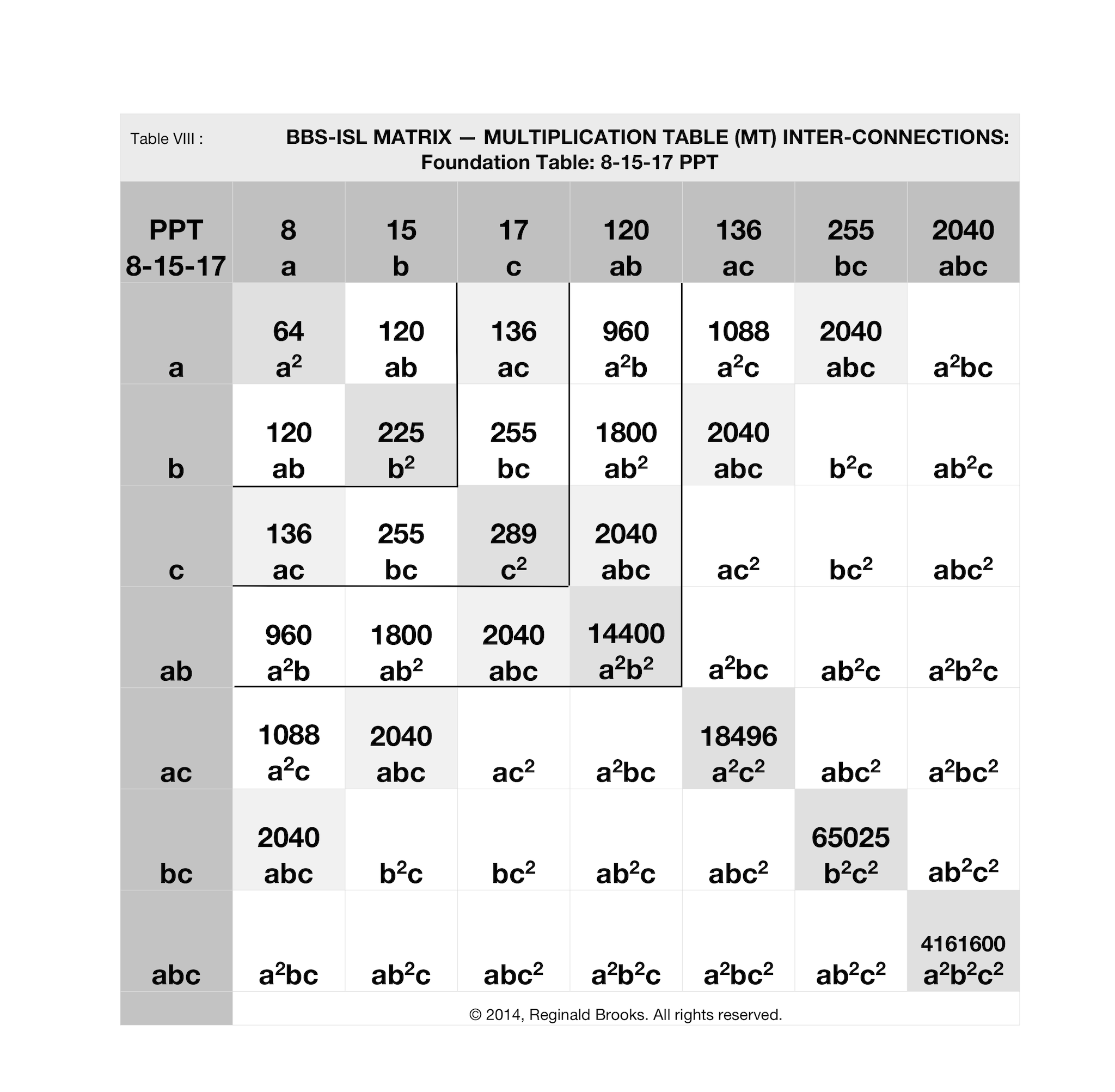
In the 8-15-17 PPT above in Table VIII, the key cell values are:

a²=64
b²=225
c²=289
ab=120
ac=136
bc=255
abc=2040
a²b²=14400
a²c²=18496
b²c²=65025
a²b²c²=4161600

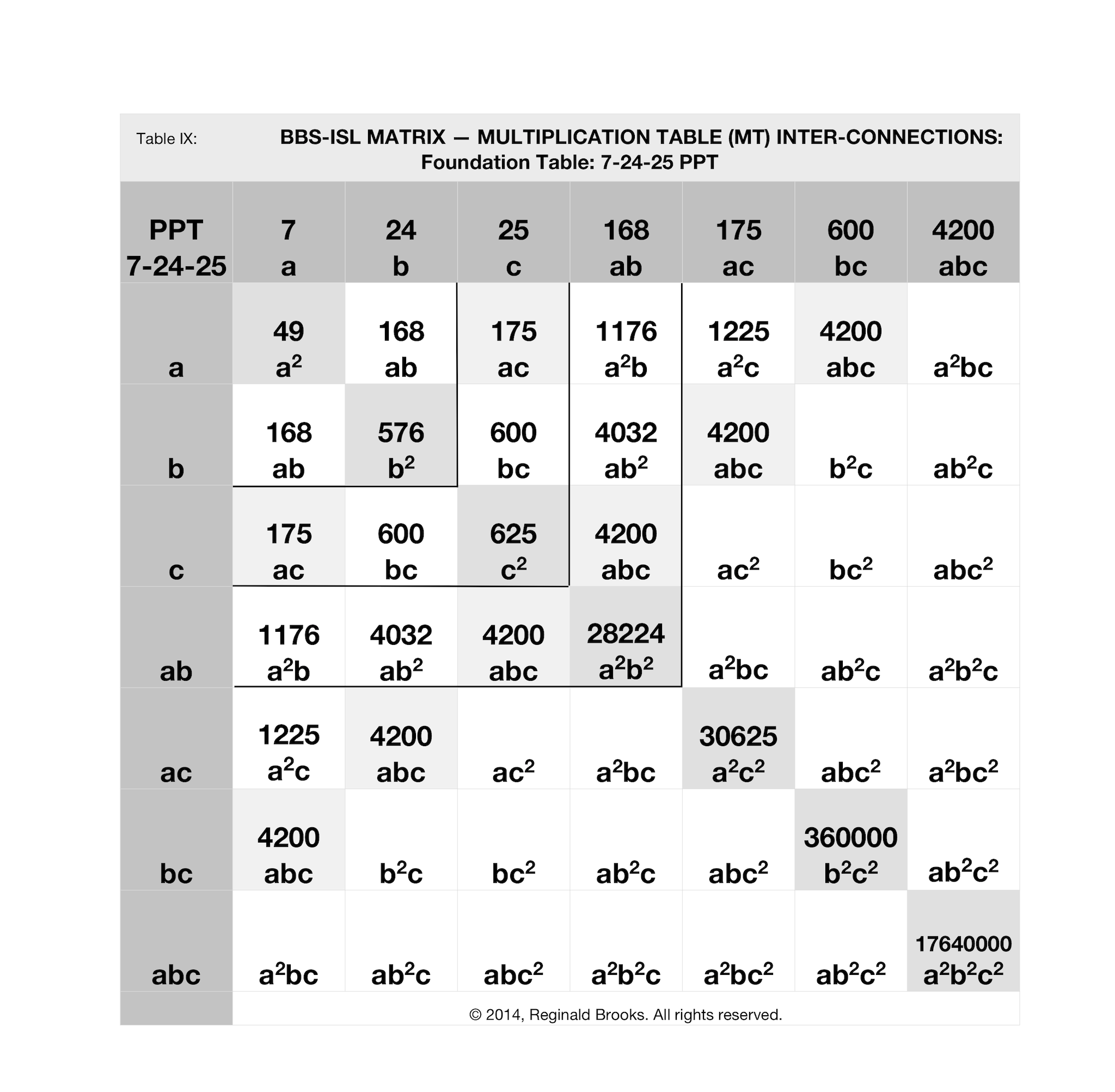
In the 7-24-25 PPT above in Table IX, the key cell values are:

a²=49
b²=576
c²=625
ab=168
ac=1225
bc=600
abc=4200
a²b²=28224
a²c²=30625
b²c²=360000
a²b²c²=17640000

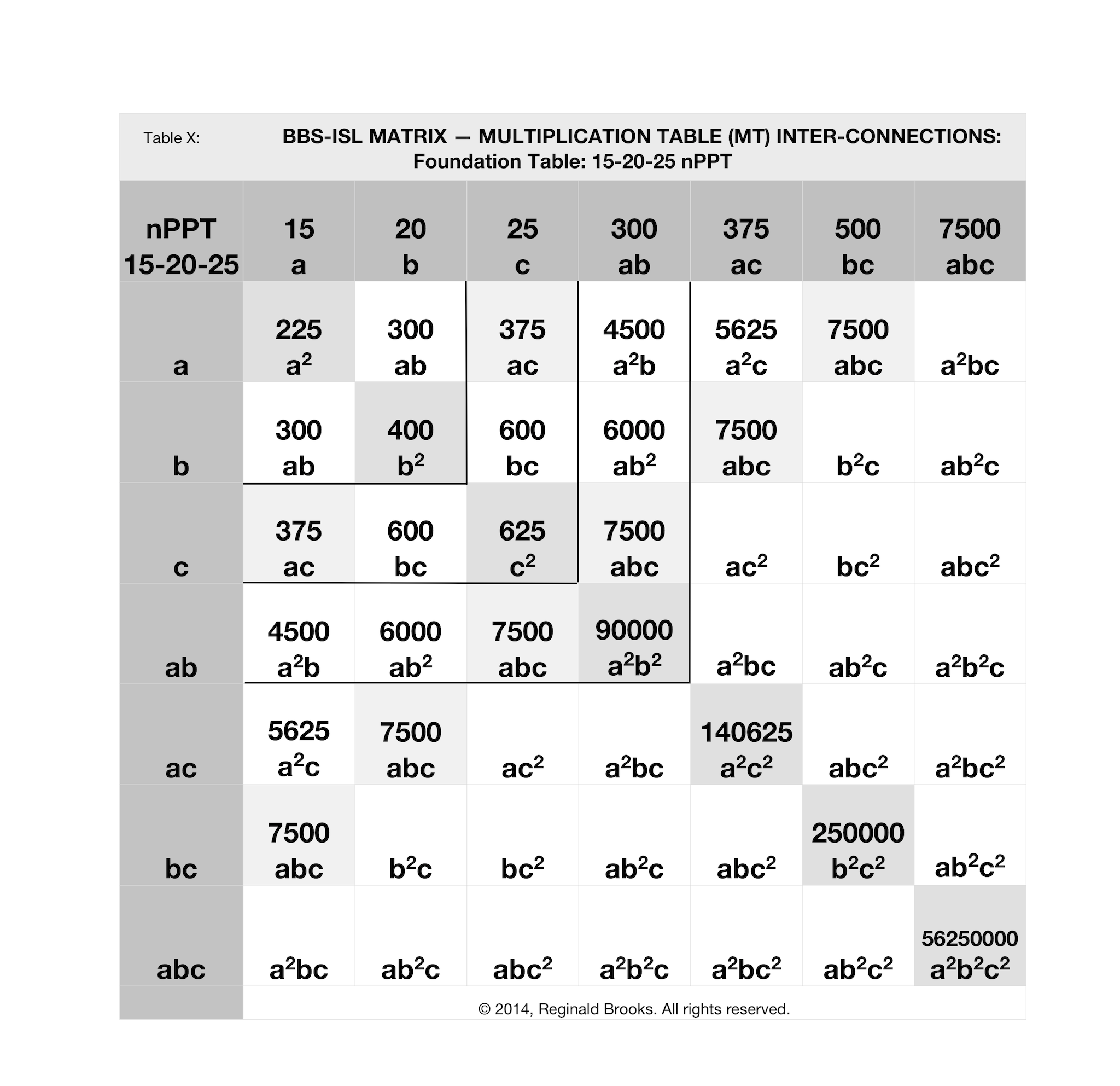
In the 15-20-25 nPPT above in Table X the key cell values are:

a²=225
b²=400
c²=625
ab=300
ac=375
bc=600
abc=7500
a²b²=90000
a²c²=140625
b²c²=250000
a²b²c²=56250000

The cell values for the first 15 PTs — PPT and nPPT — have been compiled again in Table XI below, now with a few “Additions.” These additions are literally taking the sums,∑, of a + b + c. When these sums are divided into the products of a x b x c — abc — yet another bit of interrelated information is acquired.

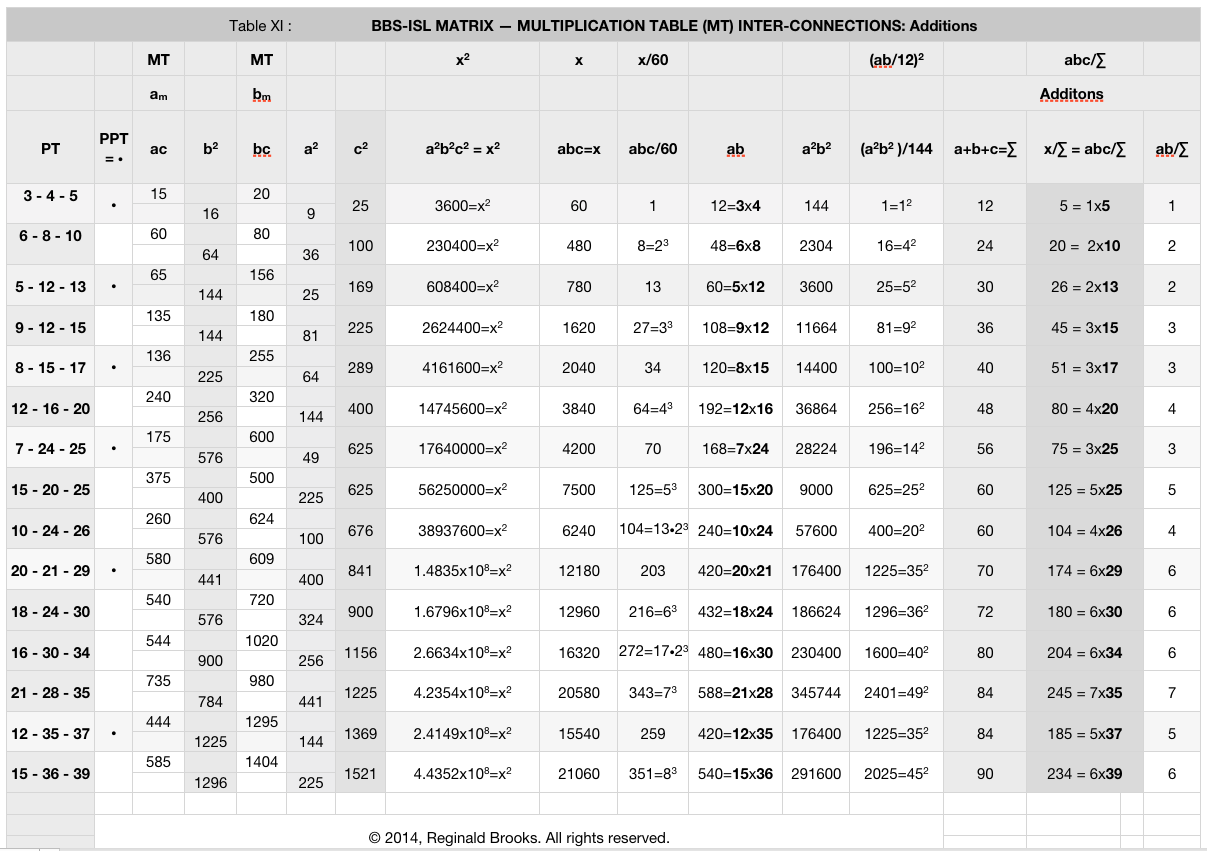
The 3-4-5 PPT is uniquely distinguished in several ways:

It is the smallest PT — PPT or nPPT
It is the only PT whose product of its two shorter SIDES — ab =3 x 4 = 12 equals the sum, ∑, of all three SIDES — a + b + c = 3 + 4 + 5 = 12
It is the only PT whose ∑ of all three SIDES x its hypotenuse, equals the product of three SIDES — ∑c = (a+b+c)(c) = (3+4+5)(5) = 60 = abc
It is the only PT whose a²b² product — (3)²(4)²=144 — equals the square of the ∑ of the three SIDES a+b+c— (3+4+5)²=144
It is the only PT whose (ab)(ac)(bc) product, or a²b²c² — (12)(15)(20)=(9)(16)(25)=3600 — equals c, the hypotenuse, when divided by (a+b+c)² — 3600/(12)²=25.

Yes, some of these findings are the result from simply rearranging the parameters, as one result follows from the other. And yet, this is uniquely true for the 3-4-5 PT.

Yes, dividing a number by itself will always result in 1. This was shown in several columns to spotlight the uniqueness of the 3-4-5 PT. All other PTs — PPT and nPPT — are multiples of the 3-4-5 PT. They can be factored down to the 3-4-5. In the x/60 column, we can see that all subsequent PTs, when divided by 60, are 8, 13, 27, … times that of the 3-4-5 value. All whole integer numbers. Notice, also, that here, the nPPT have an exponential factoring connected to their values, the PPT do not.

Under the column a²b²/144, all subsequent PTs, after the 3-4-5, when divided by 144, are 16=4², 25=5², 81=9²,… times that of the 3-4-5 value. Here, there is no difference between PPT and nPPT as to exponential factoring.

For example, the 5-12-13 PT is 13x the 3-4-5 PT for abc — 780/60=13 for the 5-12-13 and 60/60=1 for the 3-4-5. Its (a²b²⁾/144 value is 25=5² times that of the 3-4-5 PT value of 1. The 5-12-13 PPT, nor any of the other PTs, does NOT enjoy the unique properties of the 3-4-5 (listed above.)

An inter-connection between the products and sums of the 3-4-5 PT and all other PTs has been found. A single, unique 3-4-5 PT informs all other PTs.

What about predictions? Extensive analysis may reveal a pattern leading to predictions of any and all PTs. Right now, the structural pattern of the BBS-ISL matrix itself is the best visual lead we have.

As stated earlier, the even numbers within the Inner Grid of the BBS-ISL matrix are ALL divisible by 4.
Every row that contains pair-sets of squared PD numbers thereby also contains a PT — one PT for each pair-set.
All PTs have c² on the PD.
The hypotenuse values of every PPT — but NOT nPPT — are separated from each other by differences of 4x.
The PD sequence follows a difference, ∆, of 1-3-5-7-9-11… the odd-number sequence that defines the ISL
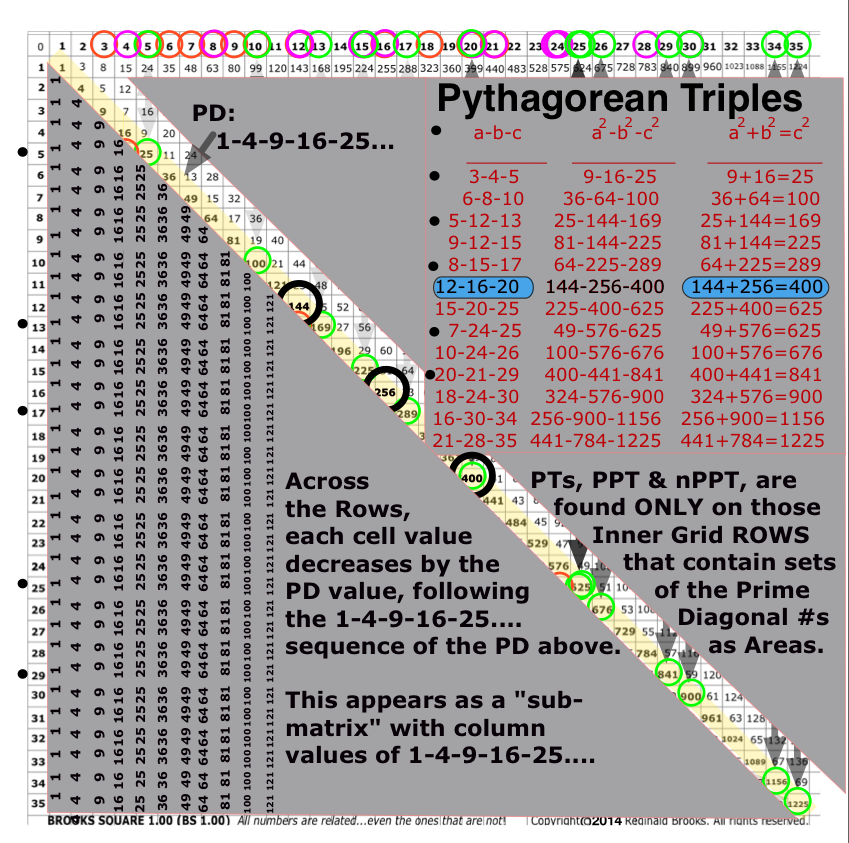
The Row sequence always follows a ∆ of (-1 from PD number), −3, −5, −7, −9, −11,…from the subsequent value.
The ∆ between the PD and each Row sequence number follows 1-4-9-16-25-36-…, or that of the PD sequence itself.

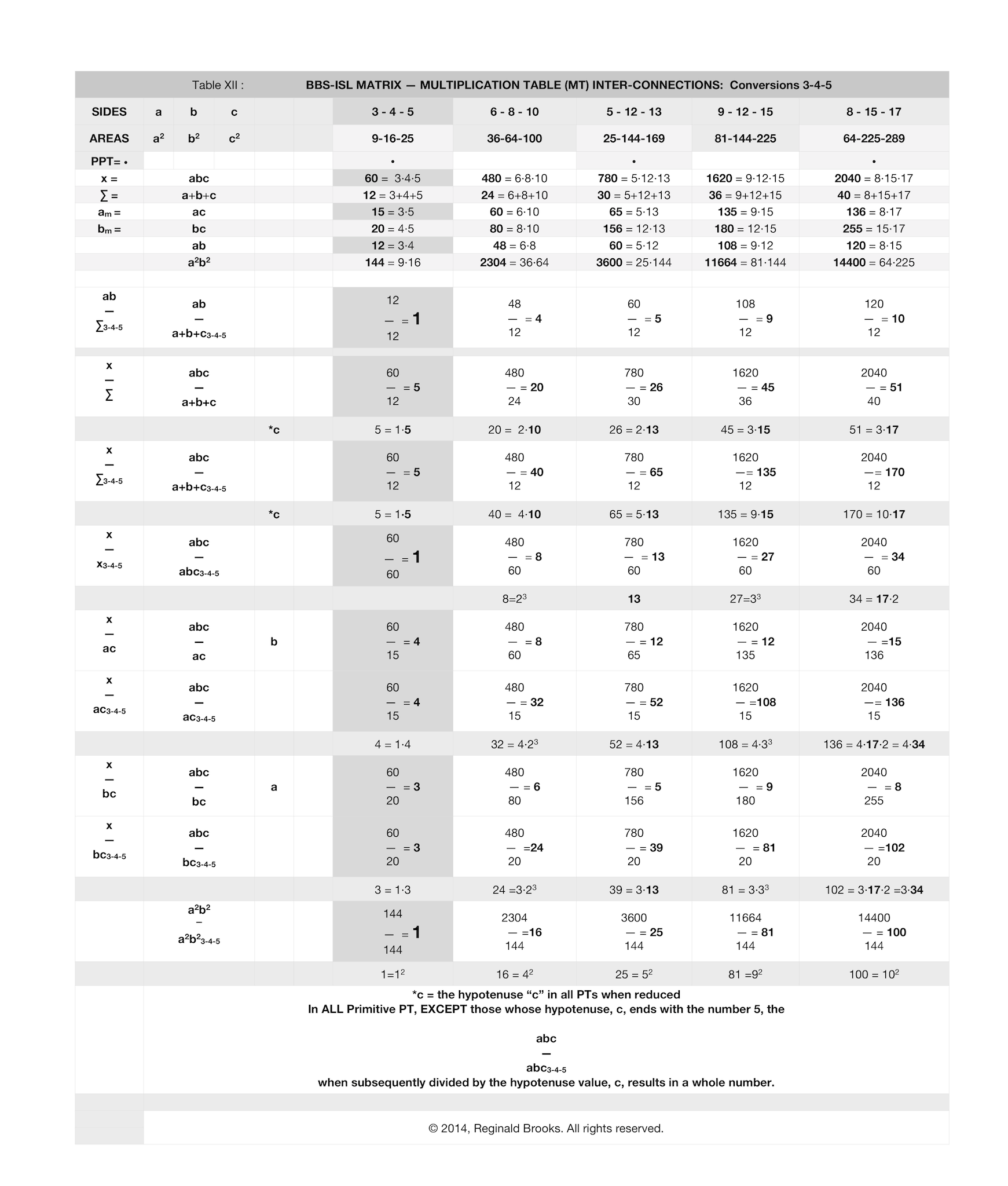
Image Reference 9

Webpage: Animated Gif, Slideshows, Movies and Images

(These 5 links all go to the same webpage)

Table XII summarizes the conversion from the 3-4-5 PPT and the next four larger PTs. The inter-connections between all subsequent PTs and the very fundamental 3-4-5 PPT is explicit. While all PTs — PPT and nPPT alike — are interrelated back to the 3-4-5 PT, some parameters separate out the Primitives from the non-Primitives.

This Image shows the rhythms of the 3-4-5 AREAS. The Orange-SIDE-3, Purple-SIDE-4, and Green-SIDE-5 AREAS are gridded out across the BBS-ISL matrix. The significant numbers of the Foundation Table are in bold.

Both Table and Image will reward some quality study.

Ultimately, these inter-connections lead back to the very basic question: What is the underlying structure of the BBS-ISL matrix that gives rise to these connections?

Well, here it is in a nutshell:

Every Row is defined by the PD sequence.
The PD sequence is defined by the sequential squaring of the whole numbers 1,2,3….
The difference, ∆, in the PD sequence follows the odd number sequence 1,3,5….
The running sums, ∑, of those odd number ∆s in the PD sequence equals the PD number values, e.i. 1+3=4, +5=9, +7=16, +9=25,… giving the 1-4-9-16-25-… sequence.
The number sequence in every Row follows this pattern:
PD# −1, PD# −4, PD# −9, PD#−16, PD# −25, PD# −36, PD# −49, PD# −64,… until it reaches the PD itself.
On certain rows, this constant Row pattern results in some of the numbers so generated being of the same 1-4-9-16-25-36-49-64-… PD series.
These select numbers always occur in pair-sets.
The pair-sets occur because the actual select number is always opposite its 1-4-9-16-25-…series, with the other number in the pair-set being the complement.

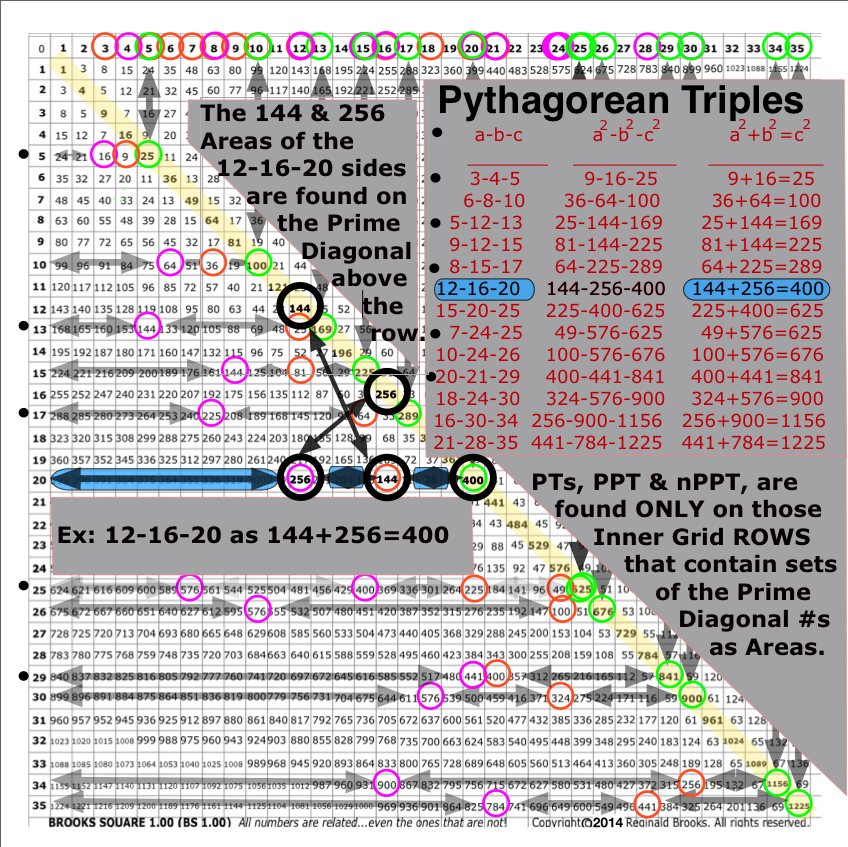
Example: 3-4-5 has:

25-1=24,

25-4=21,

25-9=16*,

25-16=9* Row sequence values. Notice that the last *two values criss-cross in value with the PD sequence values. This is a PT. The Row values of 16 + 9 = 25 is b² + a²=c².

Example: 6-8-10 has:

100-1=99,

100-4=96,

100-9=91,

100-16=84,

100-25=75,

100-36=64*,

100-49=51,

100-64=36*,

100-81=19 Row sequence values. Notice that the *36–64 and *64–36 values criss-cross. The Row values of 64 + 36 = 100 is b² + a²=c².

Example: 5-12-13 has:

169-1=168,

169-4=165,

169-9=160,

169-16=153,

169-25=144*,

169-36=133,

169-49=120,

169-64=105,

169-81=88,

169-100=69,

169-121=48,

169-144=25* Row sequence values. Notice that the *25–144 and *144–25 values criss-cross. The Row values of 144 + 25 = 169 is b² + a²=c².

And so it goes. The PD driven BBS-ISL matrix simply defines the pattern and that pattern simply defines the Pythagorean Triples! If a SQUARE number appears within the matrix, it is always part of Pythagorean Triple.

Image Reference 10

Webpage: Animated Gif, Slideshows, Movies and Images

(These 4 links all go to the same webpage)

Image Reference 10

Webpage: Animated Gif, Slideshows, Movies and Images

(These 4 links all go to the same webpage)

Image Reference 10

Webpage: Animated Gif, Slideshows, Movies and Images

(These 4 links all go to the same webpage)

Image Reference 10

Webpage: Animated Gif, Slideshows, Movies and Images

(These 4 links all go to the same webpage)

Since all PTs are defined this way: what defines the Primitive versus non-Primitives?

All Primitives have one leg SIDE ODD, the other EVEN, and an ODD number hypotenuse.
This results in their AREAS being ODD-EVEN-ODD, as well.
All Primitives, therefore, have their c ending in 1/3/5/7/9 and their c²ending in 1/5/9.
And since the difference, ∆, between any two ODD number is always an even number, divisible by 2, we have the reason the Primitive’s c and c² are always separated by 4x, or really, that is just 2x when reduced.
Non-Primitives can be either ODD-EVEN-ODD or EVEN-EVEN-EVEN and being multiples of the Primitives, this mix results in the non-Primitives NOT following the strict 2x difference between either other Primitives or non-Primitives that the Primitives always do.
All non-Primitives, therefore, have their c ending in 1/2/3/4/5/6/7/8/9/0 and c²ending in 1/4/9/6/5/0 as the PD goes: 1-4-9-16-25-36-49-64-81-100….
There are only 6 ending “ones” column numbers on the PD: 1-4-5-6-9-0 and they follow a symmetrical and repeating pattern: 1-4-9-6-5-6-9-4-1-0-1-4-9-6-5-6-9-4-1-0… numbers that are ALL used by the non-Primitives, but of that, ONLY the 1, 5 or 9 are used by the Primitives as c².
Restated: While the non-Primitives enjoy all six possible ending “ones” column numbers for c², the Primitives exclusively use ONLY 1, 5 or 9. Any SQUARE ending in 4, 6 or 0 is a non-Primitive Pythagorean Triple.
See Rules 191- 200 in the Appendix B of Brooks (Base) Square and The Inverse Square Law
(http://www.brooksdesign-ps.net/Reginald_Brooks/Code/Html/ISL/Brooks_(Base)_Square/VI.Appendix/BS-AppB.htm)
for more…

Lastly, for those wishing to delve deeper, taking a closer look at the role of the PD in defining not only the entire BBS-ISL matrix grid but the whole spectrum of Pythagorean Triples, here is a more detailed look. Herein lies the Rosetta Stone!

Image Reference 11

Webpage: Animated Gif, Slideshows, Movies and Images

The link below spotlights the various documented ways to generate Pythagorean Triples.

Formulas for generating Pythagorean triples

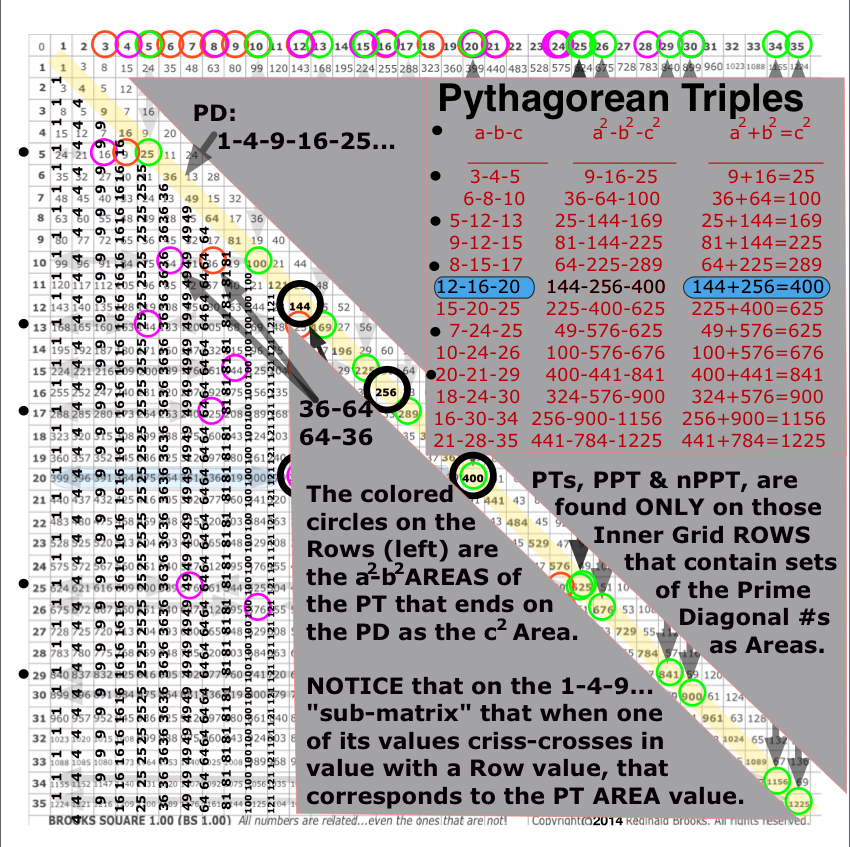
Although the Pythagorean Trees and Fibonacci Boxes are of special interest, it was Dickson’s Method for generating ALL PTs that drew notice — including Josef Rukavicka’s (2013) simple proof. Notice that his s, t values for each PT are in fact equivalent to the number of STEPS from the PD to the a²,b² AREA Squares on the given Row defining that said PT! Again, the AREAS and SIDES criss-cross complement each other as shown in Table XIII.

Dickson’s Method states: “To find integer solutions to , find positive integers r, s, and t such that is a square.

Then:

”

As “ is any even integer and that s and t are factors of .”

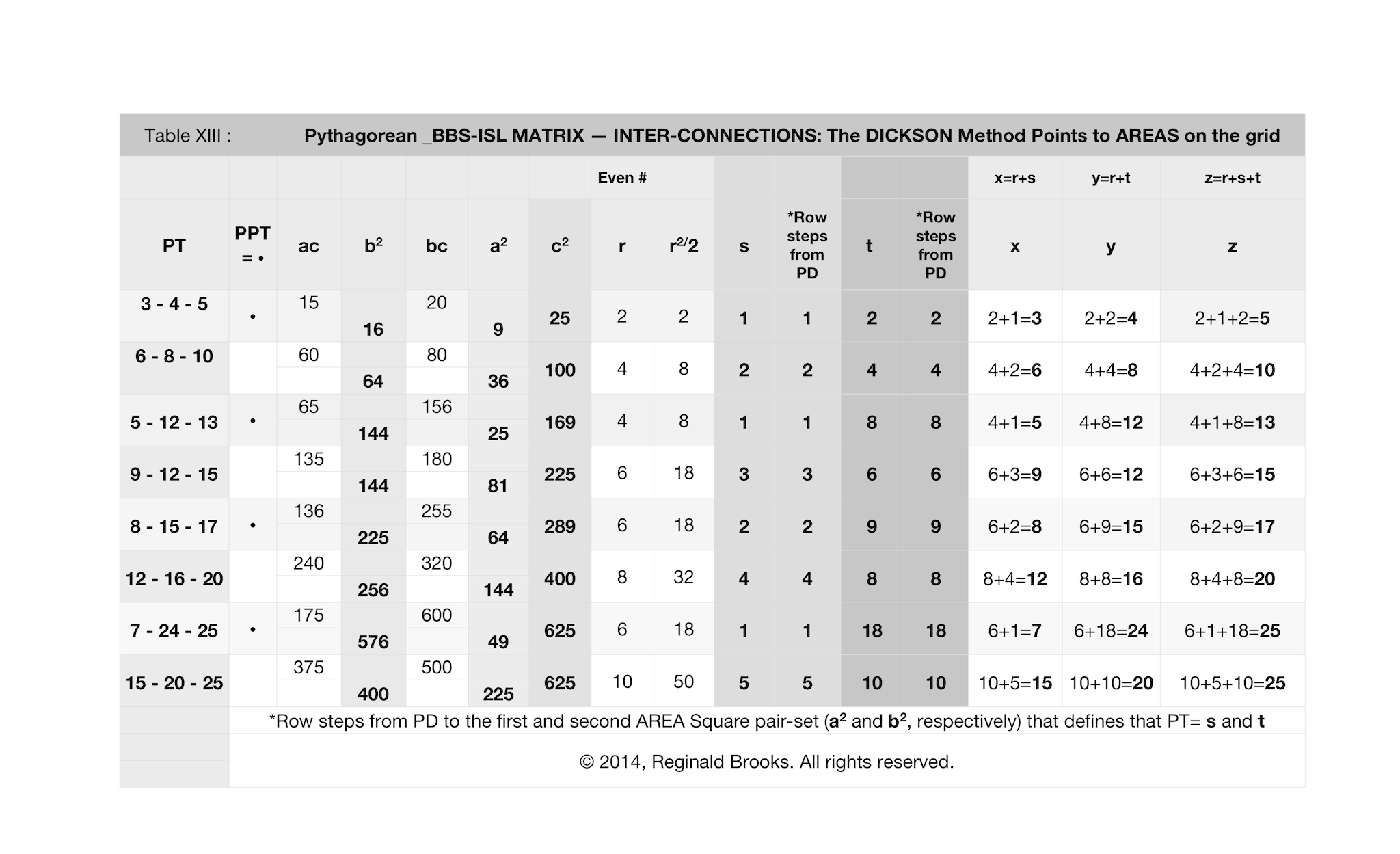
TPISC AREA Proof, Row Distribution and Inter-relationships with the Dickson Method for generating Pythagorean Triples image shown below reveals an intriguing connection.

The r, s, t parameters that his method utilizes refer directly to the SIDES values of a-b-c, yet when plotted out graphically with the usual BBS-ISL matrix AREAs approach, one quickly sees that these r, s, t values point to the number of STEPS along the pathways — pathways along the Row, the Column, and the PD — to reach those same a-b-c values. And, these point not to the SIDES but rather to the AREA values, reversing the “a” with the “b” and the “b” with the “a” parameter. Once again, the uncanny manner in which the BBS-ISL matrix visually reveals the relationships between numbers only begs further research!

Image Reference 0

(Pythagorean_BBS-ISL_Dickson.png)

Simplification!

Knowing that the Dickson Method works, knowing that the BBS-ISL matrix shows ALL PTs, and now knowing that the Dickson Method is pointing to key PT arrangements on the BBS-ISL matrix (as just shown), a true simplification is in order. As the images below shows:

What initially looks confusing is really quite simple once we keep the references straight.
As before, one must always keep in mind whether the reference is to SIDES or to AREAS.
This becomes easier to keep straight on the matrix when one realizes that because the AREAS are made from the SIDES, and, because the grid has number sequences that go logically in one direction or its opposite depending on the parameter — including up and down Columns and Diagonals, and forward and back across Rows.
And now, with the connection with the predictive powers of the Dickson Method, one must distinguish between his r, s, t values as they relate to the Row (and Column) and Diagonal AREA values that translate into a-b-c or a²-b²-c² values delineated as STEPS — and this is key — as STEPS between the AREA values.
The Dickson Method not only generates ALL PTs, it directly provides a roadmap to their disposition on the BBS-ISL matrix.
The s, t directly — and the r, indirectly as the even number that satisfies r²/2=st — gives the factors or STEPS between the PD and the two side AREAS for each and every PT.
This may be seen in either of two ways on the matrix: Along a Row (or Column) and as an AREA change in the manner of the PT Proofs.
In the Row format, the STEPS of s,t go from the PD (c²) back along the Row towards the Axis, picking out a² (as s) and b² (as t).
In the PT AREA Proof format, the STEPS of s,t go from the full 2D AREA of either a²—>c² (for t) or from b²—>c² (for s).
Keep in mind that s,t reference to a-b or b-a change because they are about STEPS and the STEPS counting along the Rows is reverse of that from the PT AREA Proof format — it is simply the STEPS that matter in the matrix grid roadmap.
A pattern of STEPS follows sequentially from each Primitive to each subsequent child sibling as:
3-4-5 is 1,2—2,4—3,6—4,8—… for siblings 6-8-10, 9-12-15, 12-16-20;
5-12-13 is 1,8—2,16—3,24—4,32…for siblings 10-24-26, 15-36-39, 20-48-52;
8-15-17 is 2,9—4,18—6,27—8,36… for siblings 16-30-34, 24-45-51, 32-60-68 and so on.
As r is an even number, taking r²/2 and further dividing by 2 — i.e. r²/4 — brings out the 1-4-9-16-25… PD sequence that the entire BBS-ISL matrix revolves around!
The real beauty of this simplification is that on a simple graphic upon the BBS-ISL matrix one has both formats — Rows and Proofs — built into the grid covering every possible PT!

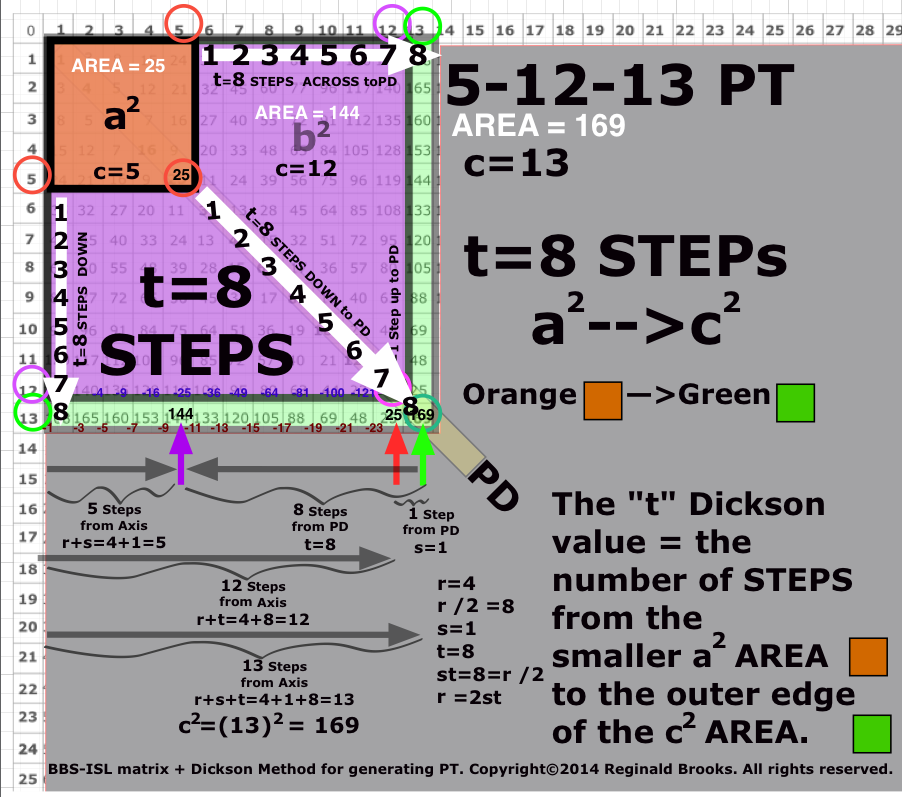
Image Reference 0

((Pythagorean_BBS-ISL_Dickson2.png)

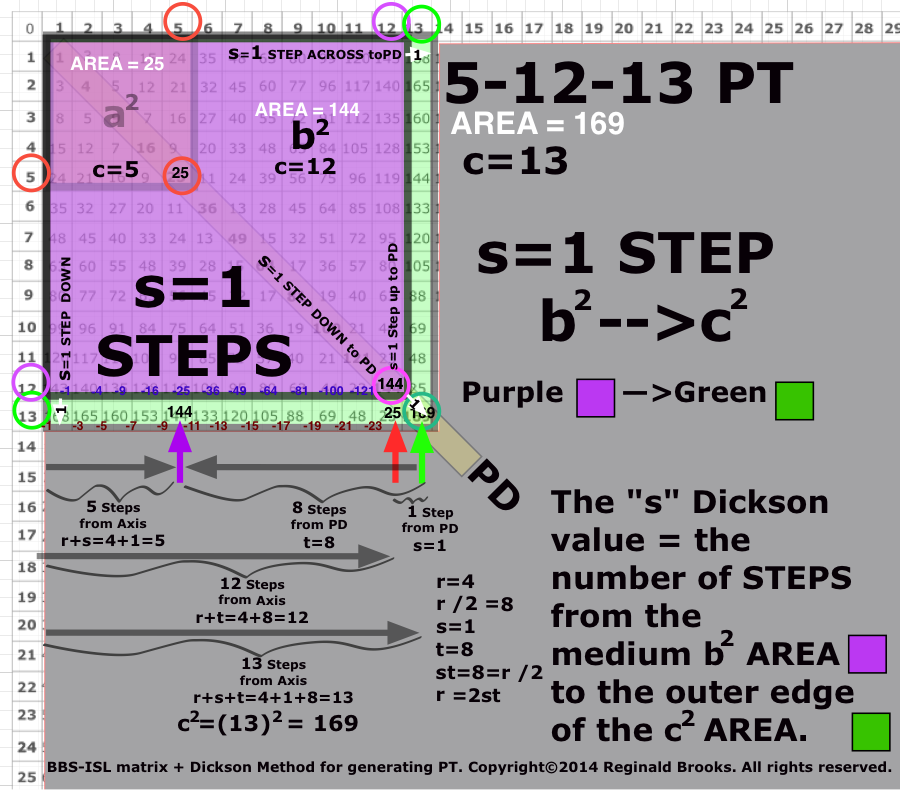
Image Reference 0

(Pythagorean_BBS-ISL_Dickson3.png)

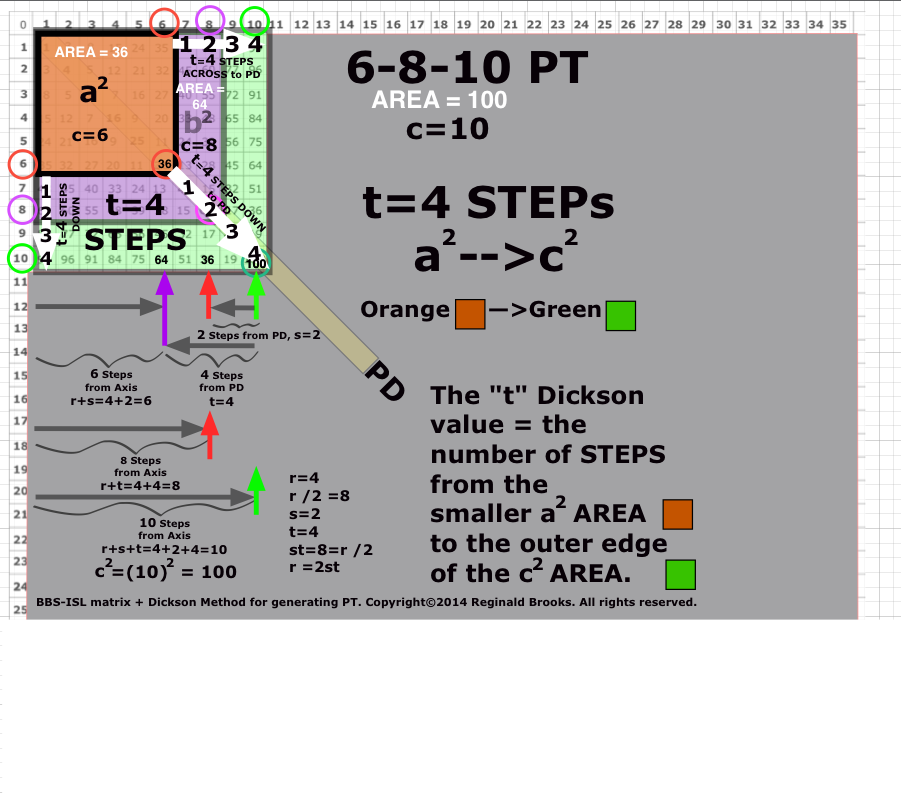
Image Reference 0

(Pythagorean_BBS-ISL_Dickson4.png)

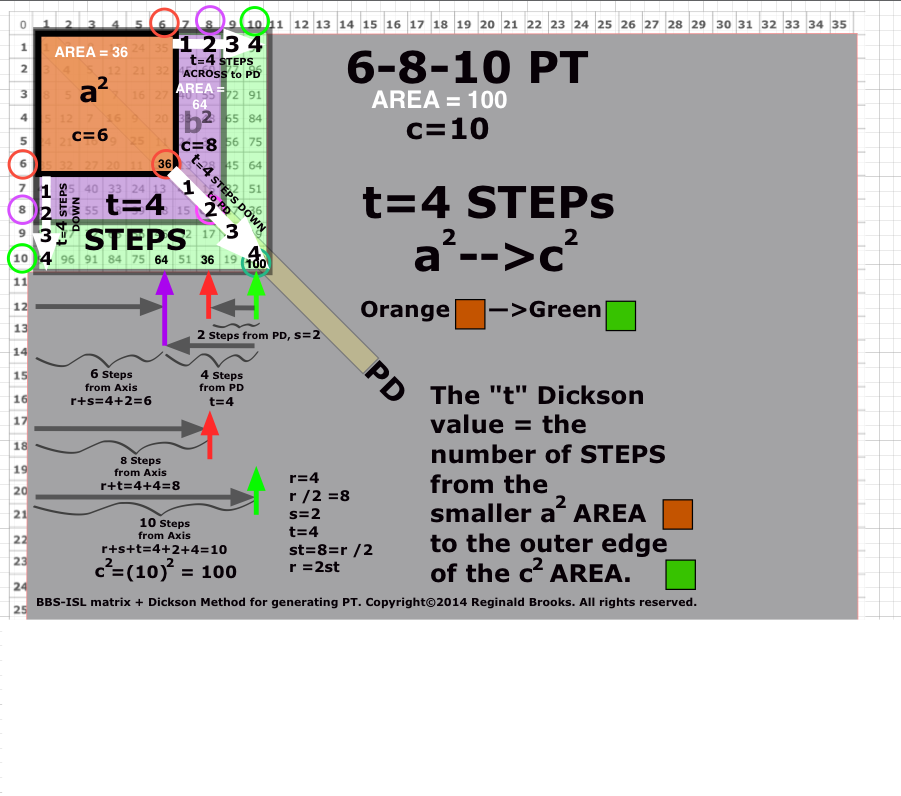
Image Reference 0

(Pythagorean_BBS-ISL_Dickson5.png)

Table XIV. The BBS-ISL matrix - Dickson Method Master Chart summarizes the information presented.

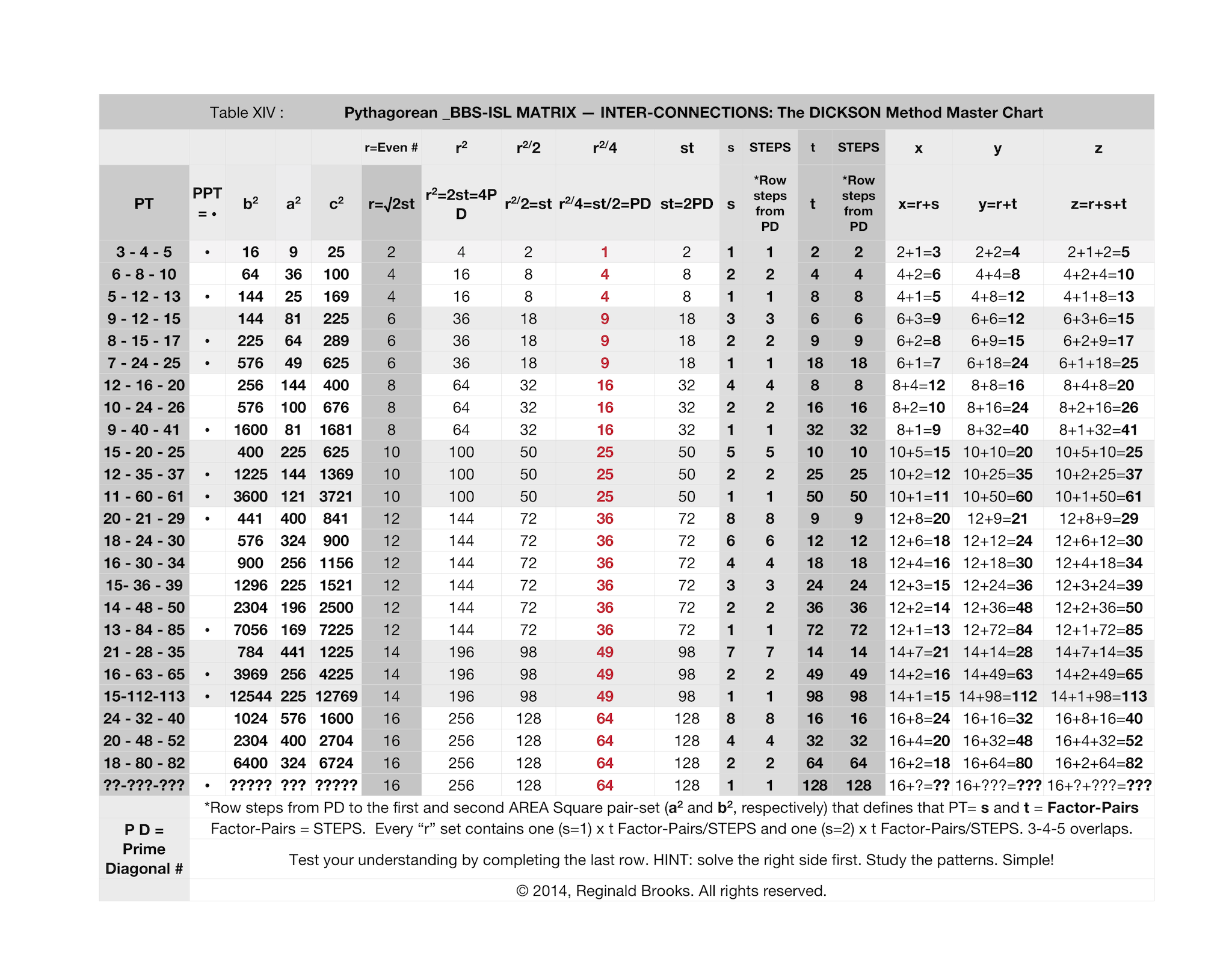
If you start with a blank page, using the Dickson Method, you can calculate All PTs by r= even numbers, such that r²=2st.

If you start with the BBS-ISL matrix, you can find All PTs by picking out the PD pair-sets on the Rows (or Columns).

The BBS-ISL geometric presentation of All PTs appears in three forms:

As Row (or Column) listings of the AREAs of All PTs.
As Row x Column actual AREA Proofs of All PTs.
Above a minimum size, All PT SIDES are shown Diagonally.

Overlapping the two methods — algebraic and geometric — one sees that they end with the same PT. The Dickson Method’s s,t values pointing to the STEPS or Factor-Pairs between the Legs and Hypotenuse of a given PT.

Whereas without the Dickson Method, one found the PTs by scanning all the Rows (and Columns), now with the Dickson Method, one has the added benefit of the s,t Factor-Pairs informing which Rows (and Columns) will contain them. The pair-sets of the BBS-ISL matrix format are just the Dickson Factor-Pairs/STEPS that are contained — and numerically allowed — in any active PT Row (or Column) leading up to its PD as c² value.

Notice in Table 14, how the Dickson Method of r²/2=st, when further divided by two, as in r²/4= a PD number. The natural sequence progression of the r=an even number falls into sets of 1-4-9-16-25-36-49-64… relating directly to the very structure of the BBS-ISL matrix.

Notice that every such set, with the exception of the first, always has a minimum of two Factor-Pairs: A base of s=1 and s=2. The first set, the r=2 that forms the 3-4-5 PPT contains both the 1 and 2 factors in its one Factor-Pair. This overlap precludes it having any more Factor-Pairs.

For example, pick a random even number, say 6 (r=6), and apply r²/2=st to get (6)²/2=18. Factor-Pair this and you get:

18=3x6
18=2x9
18=1x18

Now you know that there are 3 PTs in this set. Scan the grid visually, or, place straight lines *up the Inner Grid between 1, 2 and 3, and separately between 18, 9 and 6 STEPS in from the PD. The two straight lines will tend to converge at the top. Your 3 PT Rows will cross these lines. The difference between Factor-Pairs is, of course, the difference in STEPS between the two AREA Squares of a²-b² of that PT.

Remember that while the s,t sets are Multiplication Factor-Pairs of Dickson’s r²=2st, they translate to Addition STEPS, additional STEPS between PD and the leg-AREA Squares. Those AREA Squares are Added together to form the PD AREA Square of the hypotenuse. Dickson’s Method ultimately rejoins the r,s,t values by addition, as well, to reach the same spot.

This all becomes incredibly simple once one gets familiar with the process!

*Start with the 1-18 first and work back up the grid. Lines will ultimately converge.

Image Reference 0

(Pythagorean_BBS-ISL_Dickson6.png)

Inter-Connections

In this brief section, a quick look at TPSIC and the BBS-ISL matrix in different BASEs_ will reveal an even deeper connection.

As the previous section on the Distribution of the PTs has shown, there is a very deep connection — an inter-connection, if you will — between the PTs and the very structure of the BBS-ISL matrix. There are no coincidences.

And while the earlier section on the visualization and proof of any PT directly on the BBS-ISL matrix was shown to be simple, direct and even intuitively obvious — that is, easily discoverable — once one brought the PT idea to the matrix table, digging deeper into the mechanics of distribution certainly added some mystery back.

Sure, one can state and easily see that (*most) every PT is presented on the BBS-ISL matrix in one of two ways.

First as SIDES, the a-b-c values of ALL nPPTs are shown as diagonally linked arrays of triple sets. Because the matrix Strict Inner Grid contains NO prime numbers, nor any even numbers not divisible by four, only the multiple siblings of the Primitives are revealed. Parallel and perpendicular to the PD, these SIDES are nearly ubiquitously patterned over much of the entire matrix grid.

Second, as AREAS, the a²-b²-c² —as b² + a² = c² — absolutely ALL PTs are revealed on select Rows (and Columns) of the grid, with b² and a² on the Row culminating with c² on the PD. This AREA presence is both simple, direct and intimately tied to the underlying mechanics of the BBS-ISL matrix .

A. BASE_2_3_4_5_6_8_10_PT

What about other inter-connections? Can they shed some new light on how to think about the distribution — and, ultimately the inter-connection — between the PTs and the BBS-ISL matrix?

The ISL, the foundation of the BBS-ISL matrix, is fundamentally based on distribution — the distribution of quantity. That quantity may be a composite parameter like force, energy or other influence, or it may be the measuring mechanism itself like the area or volume geometry.

The BBS-ISL enumerates the ISL-base quantities as whole number integers within an ever-expanding matrix grid.

That matrix is enumerated in our common BASE_10 system: 0-1-2-3-4-5-6-7-8-9.

What about enumerating in other BASEs_ like BASE_2_3_4_5_6_8? Does the BBS-ISL matrix in other BASEs_ still hold up?

The answer is YES. The quantity relationship inter-connections that form the basis of the matrix remain intact regardless of the counting system.

Does the examination of the PT AREA distribution in the BBS-ISL matrix in other BASE_ counting systems reveal any clues as to the distribution of the PTs — PPT and nPPT?

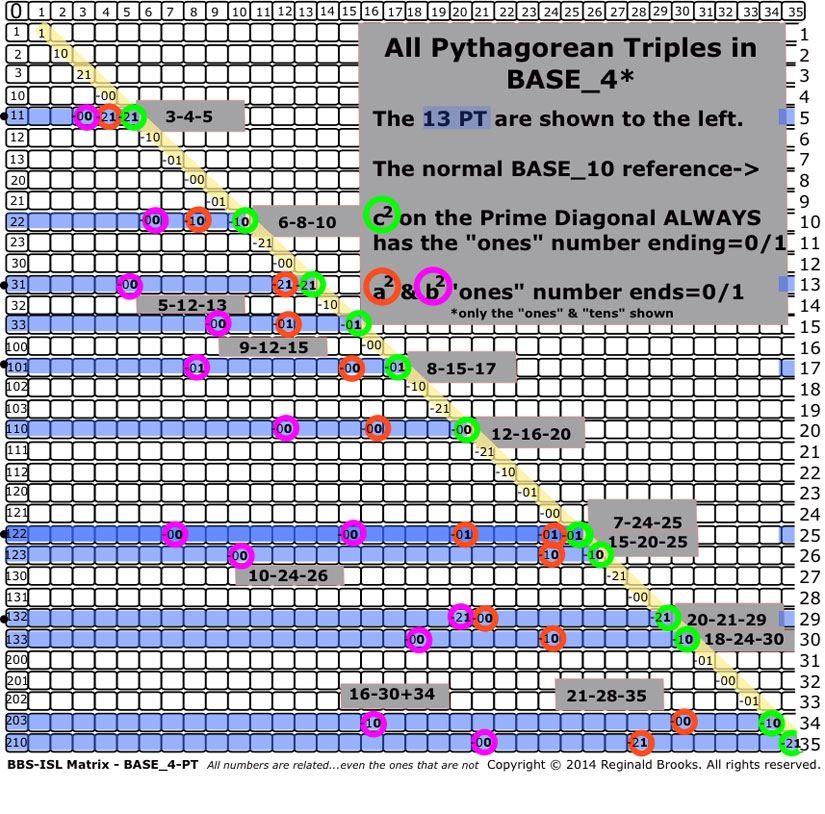
The answer is YES. Examination of the PTs across BASE_2_3_4_5_6_8_10 reveals select pointers to the PTs in general and to specific pointers exclusive to the PPTs. BASE_5 tended to be more mixed, as in BASE_10.

As presented above, the PPT AREAS value c² only ends with 1/5/9 in BASE_10. It only ends in 1 in BASE_2_3_4_6_8 as examined in all PTs with c² up to 10,000. Looking at the c=hypotenuse SIDE values, Primitives always end with 1 in BASE_2_4; end in either 1/2 in BASE_3, and end in either 1/5 in BASE_6_8.

It would appear that in order for a Primitive Pythagorean Triple to form, both of two requirements must be met:

1. Based on c = hypotenuse (SIDE)

BASE_2=1

BASE_3=1/2

BASE_4=1

BASE_6=1/5

BASE_8=1/5

2. Based on c² = hypotenuse² (AREA)

BASE_2=1

BASE_3=1

BASE_4=1

BASE_6=1

BASE_8=1

The non-Primitive Pythagorean Triples overlap these specific pointers but do NOT satisfy both conditions.

*Since the PT SIDES contain even numbers not divisible by 4 and/or prime numbers, and, the BBS-ISL matrix grid contains neither, only multiple siblings appear.

B. BASE_3

~BASE_3~

Image Reference 12

Webpage: Animated Gif, Slideshows, Movies and Images

C. BASE_4

~BASE_4~

Image Reference 8

Webpage: Animated Gif, Slideshows, Movies and Images

D. BASE_5

~BASE_5~

Image Reference 13

Webpage: Animated Gif, Slideshows, Movies and Images

E. Circle-Pentagon Displays

~Circle-Pentagon Displays~

Image Reference 14

Webpage: Animated Gif, Slideshows, Movies and Images

The interesting — and, perhaps, not so interesting — thing about the Circle Displays is how completely untuned they are to any specific meaning.

Take any long enough sequence of random whole number integers in BASE_10 (0-1-2-3-4-5-6-7-8-9), which is what we are using, and it will naturally form the double pentagram/pentagon (decagram/decagon) pattern. If that starting random sequence is reduced to just 5 of the 10 numbers — as in 1-3-5-7-9 (ODDS) or 0-2-4-6-8 (EVENS) as in the 1^st number “ones” of the various Diagonals parallel to the PD in the BBS-ISL matrix — only the single pentagram/pentagon forms. The same occurs visually, if the 6 numbers of the PD/Row/Column are used, in that the two ends of this symmetrically repeating pattern are separated by only one number. Visually, this is masked in the composite view.

Nevertheless, the extraordinary beauty of the decagram is witness to the beauty of Nature first hand. First the triangle, then the circle, the square…and then the quantum jump…the pentagon/pentagram. As Nature replicates, so does her geometry. The double-pentagon provides the perfect form containing the Golden Mean/Section/Ratio, as well as all of the geometric jewels of the simpler forms below it — π, √2, etc.. No wonder it is the blueprint for DNA.

Conclusion

A lot of ground has been covered here. This might be expected when a new lens, such that the BBS-ISL matrix certainly is, comes to bear on an ancient, universal theme — the Pythagorean Triples (PT).

More than adequately covered in the literature, writings, songs and art of all cultures, it has been an attempt here to present an entirely new manner of looking at the Pythagorean Triples, their proofs, distribution and ultimately their inter-connections. As it turns out, the inter-connections with the BBS-ISL matrix are what has become the main theme. As the Inverse Square Law (ISL) upon which the BBS-ISL matrix is formed is, in many respects, one of if not the main “laws” or relationship informing principles in all of science — most especially physics and mathematics. That the PT should be so intimately born, described and proved within that matrix is not without great introspection. If the ISL is fundamentally about how influence is distributed — spread out and diluted — over SpaceTime (ST), then the Pythagorean Theorem is a natural, built-in measure of that.

Like many pivotal relationships, that of The Pythagorean - Inverse Square Connection (TPISC), one must not let the initial simplicity blind us to the deeper attributes offered. To keep things straight, one must keep in mind the distinctions between how the PTs are presented on the BBS-ISL matrix.

Typically, the a-b-c SIDES are presented Diagonally as sets of triples within the Inner Grid of the matrix.

The a²-b²-c² AREAS are presented horizontally as Rows (or vertically as Columns when looking at the upper half of the symmetrical matrix) but with a difference. The b² and a² values are on a Row (or Column) within the Inner Grid, but the c² resides on the Prime Diagonal (PD) at the end of that Row, and that is key.

While the SIDES values represent the multiple siblings of both Primitives (PPT) and non-Primitives (nPPT) and are nearly ubiquitously patterned over the entire expanding matrix grid, the AREAS values, while also representing all PTs, both PPT and nPPT, are more uniquely presented. They are presented only once upon a given Row. Even their multiple sibling nPPTs are presented, as AREAS, only once on the entire grid, at their designated Row (or Column).

It is this singular representation — or call it presentation — upon a Row (or Column) that both defines the PT and sheds light on the wheres and whys of their distribution. As the BBS-ISL matrix is defined by the odd number summation series 1-3-5-7-9… that when added sequentially become 1-4-9-16-25… (PD numbers) which is none other than the Squares of the whole number integers 1-2-3-4-5…, every PT is ultimately defined by this same propagator. As every Row (or Column) is itself defined by the PD sequence 1-4-9-16-25… — or its propagator 1-3-5-7-9… — the PTs are defined by the same. Since not every Row (or Column) has a PT, the quest becomes to determine what built-in relationships or inter-connections within the BBS-ISL matrix itself determine when a Row is hot, active, sparkling with the PT that is onboard!

For one thing, only select Rows (or Columns) contain a Squared number. When they do they always come in pairs or pair-sets. In every instance, one of these pair-sets is a PT. Once a Row is hot, duplicates occur like clockwork patterns further out on the grid.

Another clue, all Squares on the PD, and therefore all Squares on any Row (or Column) end in one of the 6 possible values 1/4/9/6/5/0, as do the nPPTs, but the PPT ONLY end in 1/5/9. Any SQUARE ending in 4, 6 or 0 is a non-Primitive Pythagorean Triple.

Detailed in the latter part of the Distribution section is a detailed look at the Dickson Method for generating ALL PTs. The a-b-c and a²-b²-c² values of PT are deconstructed down to Factor-Pair sets — sets of two factors (s,t) that when multiplied together equal r²/2, where r=an even number. The additions of the r, s, an t values for each Factor-Pair set, in combinations, will give the PT values.

Further deconstruction and overlapping with the BBS-ISL matrix has shown that the Dickson Method acts like a Rosetta Stone in that the very same Factor-Pair sets are equivalent to the STEPS separating the AREA squares of the PT on the grid.

Both the Dickson algebraic method and the BBS-ISL geometric matrix method reveal exactly the same PT. The Factor-Pairs = STEPS pair sets.

The BBS-ISL matrix method has the added advantage in that it presents ALL PTs in an AREA Proofs visual manner as well as in listing the AREAS of each PT on the Row (or Columns). Additionally, All PT SIDES (above a minimum size) are presented Diagonally over the entire matrix.

The inter-connections between these two methods are so tight that little daylight has any chance of separating the two.

Yet more clues are had when comparing the distribution of PTs in BASE_ systems other than our common BASE_10. That the Primitives once again are filtered out across the BASEs_2_3_4_6_8 further validates the true intimacy of TPISC.

Perhaps the most the most profound finding is that when the a-b-c components are broken down individually and re-examined within a multiplication grid — showing new combinations of a, b and c — that ALL PTs — PPT and nPPT — can be shown to be related to and derived from the one single 3-4-5 Primitive.

Summary: The BBS-ISL matrix reveals ALL PTs.

1. The BBS-ISL matrix displays ALL PTs and their proofs. (And it can be shown that All PTs ultimately relate back to the 1^st PPT: 3-4-5.)

2. The Dickson Method generates ALL PTs.

3. The Dickson Method decodes the BBS-ISL matrix into classes by default:

a. "Have" (Rows/Columns that "have")

b. "Have Nots" (Rows/Columns that "have not."

4. The Dickson Method only reveals the "Haves."

5. The "Haves" are Rows/Columns of the BBS-ISL matrix that have pair-sets of PD Square numbers — these are the PTs.

6. The "Have Nots" are Rows/Columns that do NOT have PD Square numbers.

7. The "r=even number" in the Dickson Method effectively factors all Square numbers for Factor-Pairs (i.e. pair-sets) and this shows on the BBS-ISL matrix as "Haves" Rows/Columns.

8. The "r²=2st=4PD" in the Dickson Method is the pathway to finding the Factor-Pairs/pair-sets for any even number=r.

9. The resulting "s,t" values equal the the Factor-Pairs in the Dickson Method, AND, the pair-sets within the Rows/Columns of the BBS-ISL matrix.

10. All PTs occupy a "Haves" Row/Column on the BBS-ISL matrix, with their distance in grid cell-STEPS from the PD being the "s,t" values of the Dickson Method marking the actual location (and thus cell value) of the two short Leg AREAS (a²+b²), whose sum = the hypotenuse AREA (c²).

~~~~~

It is ultimately the nature of how dimensions — line, area, volume —numerically interact with scaling that defines the geometry of the Universe. The addition of time dimensions, as well as additional space dimensions, via rotation, movement, scaling, included in the mix adds to the mysterious richness and complexity that issues forth. It belies us to examine the central, fundamental role that line, area, and volume play in all realizations of spacetime (ST).

The journey has been long, yet revealing. The formidable numerical relationships embedded within the BBS-ISL matrix through TPISC, The Pythagorean — Inverse Square Connection, only re-affirms the fundamental nature of the Inverse Square Law in defining the very Nature within which we exist!

Quick Links to Image Reference Pages:

References

All references are valuable. Unordered list.

Appendix A

art theory 101 / database index

titles and topics:

Page 1: The FARNIE art classification scheme.
(Formalism, Abstraction, Representation, Naturalism, Idealism, Expressionism)

Page 2: PIN: Pattern in Number...from primes to DNA.
A brief primer on visual patterns found in simple, well known number systems leading into the remarkable number magic and esthetic beauty of the DNA double helix (axial view) found in Page 3. GoDNA and continued in Page 4. SCoDNA below.

Page 2b: Butterfly Primes...let the beauty seep in.
The lure and elusiveness of prime numbers, those very same numbers which all the other natural whole numbers can be reduced to, is thousands of years in the making, captivating the minds of anyone...perhaps everyone...who has ever contemplated their beauty and mystery. Can this beauty reveal a visual and mathematical pattern? First online: 12-09-05

Page 2c: Butterfly Prime Directive...metamorphosis.
This paper provides further insight into the foundation of the "Butterfly Primes" pattern and in doing so further substantiates the proof of Riemann's Hypothesis. First online: 01-05-06

Page 2d: Butterfly Prime Determinant Number Array (DNA) ~conspicuous abstinence~.
The role of the highly ordered positive space pattern of the odd non-primes in revealing the reverse, negative space pattern of the primes as a determined number array is revealed. First online: 02-15-06

Page 3: GoDNA: the Geometry of DNA (axial view) revealed.
Which came first? The self replicating underlying geometry or the form itself with its dependence on enzymes, hydrogen bonding and a matching code of bases?

Page 4: SCoDNA: the Structure and Chemistry of DNA (axial view).
Extending GoDNA into the realm of structural detail and chemistry forming the composite design. All DNA works online: 2001.

Page 5a: Dark-Dark-Light: Dark Matter = Dark Energy (the inverse of) .
Conservation of SpaceTime as moderated by the Conservation of Force and Energy. The LUFE Matrix is introduced. The relationship between the Higgs, photon and graviton gauge bosons as the gatekeepers between spacetime and matter is examined. Date first published: 05-08-03; link to LUFE Matrix added 05-30-03.

Page 5b: The History of the Universe in Scalar Graphics .
(Simultaneous Birth of Black Holes and the Inflationary Universe at the onset of the Big Bang) A mostly graphical supplement to "Dark Matter = Dark Energy (the inverse of): The Conservation of Spacetime by The Conservation of Force". Date online: 11-28-04

Page 5c: The History of the Universe - update- "The Big Void" .
A short supplement to "Dark Matter = Dark Energy (the inverse of): The Conservation of Spacetime by The Conservation of Force" and "The History of the Universe in Scalar Graphics." Date online: 09-05-07

Page 6: The LUFE Matrix.
Here is a fully digitized and interactive version of The LUFE Matrix The LUFE Matrix: the distillation of SI units into more fundamentally base units of space and time dimensions (Short Title: The Multi-dimensional LUFE Matrix). Date first published: 1985 (LUFE); Date first published by itself: 1991. Date online: 05-30-03. Preview-Review Slide Show added 08-05-03

Page 7: The LUFE Matrix Supplement.
The supplement, first published along with the The LUFE Matrix in 1991, contains over 200 examples and proofs covering a wide range of classical and modern physics and cosmology. The paper version is 97 pages long. The digital version is now completed. Date first published: 1985 (LUFE); Date first published by itself: 1991. Date online: partial 06-30-03. Completed:07-27-03

Page 8: The LUFE Matrix: Infinite Dimensions.
~a room with a view...within a room with a view...within a room with a view~
A new, speculative journey to account for the multiple dimensions that have informed The LUFE Matrix since its introduction in 1985. Date online: partial 03-10-04. Completed: 03-14-04

Page 9: The LUFE Matrix: E=mc²
~and then some~
The focus is on energy. From Einstein's initial insight into the transformation between mass and energy, we now have a large number of similar transformations between energy and the other fundamental parameters of matter...i.e., charge and spin...and their activities within their space-time environments such as velocity and acceleration, frequency and temperature, momentum, pressure and force, potential difference, heat and work, etc. The original Preview-Review Slide Show "Can you say energy 10 different ways?" (see above), included here, is now further enhanced with a showcase of select LUFE Matrix Supplement examples all focused on the various forms that energy can take. Date online: partial 08-05-03. Completed: 10-17-05

Page10: Quantum Gravity..by the book
~merging of Quantum Mechanics with Gravity ~
How do the mechanics of a written language explain quantum mechanics and general relativity (gravity)...the merging of the very small and the very large. Could it be that the same evolutionary neural development that allowed us the creation and development of our language...and more than just mimicking the results thereof...actually was developed in the same nursery of elemental space-time physics that form our understanding of the cosmos. Simple elemental combinations produce the greatest richness and diversity within a harmonious whole. Date online: 04-10-08. Completed (Table added): 04-29-08

Page11: Conservation of SpaceTime
~The role of the Higgs, graviton and photon bosons in defining Dark Matter = Dark Energy (the inverse of) ~
In this paper, we will bring together important concepts laid out in more detail in earlier works. Specifically, we will be providing some simple visual portraits of the elementary particles. These diagrammatic illustrations will allow us to "see" how the concepts might in fact play out. Of course, what we are doing is illustrating the invisible… namely spacetime (SpaceTime=ST) itself and the matter and fields which are to populate it. As it will hopefully be clear, ST, and the matter and fields, are integrally interrelated... one defining the other and it is in the ultimate conservation of ST that results in and from the individual conservations of energy, force, and momentum. Any successful merging of the very large (general relativity) and the very small (quantum mechanics) into a theory of Quantum Gravity will have to address these fundamentals of ST. Date online: 12-31-08.

Page 12a: LUFE: The Layman's Unified Field Expose`
~Introduction-Contents-List of Figures~
A textural, visual and mathematical work that presents a clear vision of our Universe(s). More relevant today, than ever. The SpaceTime (ST) continuum ...the matter and fields that are intimately derived from ...singularities, the Planck Event Horizon, pulse generation ...the expression of mass, charge and spin and other fundamental constants ...the role of symmetry and asymmetry in the expression of ST units like the fermions and the force-mediating vector bosons ...is explored from the visible to the hidden through the interface of the photon, graviton and Higgs bosons ...the source of the fractal Universe. Date first published by itself: 1985. Date online: 11-26-08.

Page 12b: LUFE: The Layman's Unified Field Expose`
~Chapter I: Symmetry of Design (Fields) ~sonata form~~
Date first published by itself: 1985. Date online: 11-26-08.

Page 12c: LUFE: The Layman's Unified Field Expose`
~Chapter II: Introduction to the Geometry Of Interactions ~rhythms and melodies~~
Date first published by itself: 1985. Date online: 11-26-08.

Page 12d: LUFE: The Layman's Unified Field Expose`
~Chapter III: The Geometry of Elemental Forms ~scales~~
Date first published by itself: 1985. Date online: 11-26-08.

Page 12e: LUFE: The Layman's Unified Field Expose`
~Chapter IV: The Geometry of Universal Constants ~obstinate bass~~
Date first published by itself: 1985. Date online: 12-08-08.

Page 12f: LUFE: The Layman's Unified Field Expose`
~Chapter V: The Geometry of Intermediate Forms ~chords~~
Date first published by itself: 1985. Date online: 12-08-08.

Page 12g: LUFE: The Layman's Unified Field Expose`
~Chapter VI: The Geometry of Change ~polyrhythms and polyphony~~
Date first published by itself: 1985. Date online: 12-08-08.

Page12h: LUFE: The Layman's Unified Field Expose`
~Chapter VII: The Geometry of Paradox ~counterpoint~~
Date first published by itself: 1985. Date online: 12-08-08.

Page12i: LUFE: The Layman's Unified Field Expose`
~Chapter VIII: The Geometry of Large Forms ~harmony~~
Date first published by itself: 1985. Date online: 12-08-08.

Page12j: LUFE: The Layman's Unified Field Expose`
~Appendix Set I:~
Date first published by itself: 1985. Date online: 12-08-08.

Page12k: LUFE: The Layman's Unified Field Expose`
~Appendix Set II:~Fundamental Constants
These five follow-up supplemental papers, collectively called "Fundamental Constants," are very important works that present key themes which run through LUFE. For some readers, reading these shorter, self-contained works first, in reverse order, will provide the benefit of a spotlight on those key themes that will then more fully resonate with the complete LUFE read. The works are now included, in the original unaltered state from 1985-07, as part of LUFE under this Appendix Set II. Date first published by itself: 1985-87. Date online: 12-08-08.

Page12k: LUFE: The Layman's Unified Field Expose`
~Appendix Set II:~Fundamental Constant ~1. Mass
Mass expression. Date first published by itself: 1985-87. Date online: 12-08-08.

Page12l: LUFE: The Layman's Unified Field Expose`
~Appendix Set II:~Fundamental Constant ~2. Ratios
Ratios of the Electron and the Proton. Date first published by itself: 1985-87. Date online: 12-08-08.

Page12m: LUFE: The Layman's Unified Field Expose`
~Appendix Set II:~Fundamental Constant ~3. Charge
Charge expression. There are particles (ST units) with mass and no charge, but never with charge without mass! Date first published by itself: 1985-87. Date online: 12-08-08.

Page12n: LUFE: The Layman's Unified Field Expose`
~Appendix Set II:~Fundamental Constant ~4. The LUFE Matrix
Common units and The LUFE Matrix. Date first published by itself: 1985-87. Date online: 12-08-08.

Page12o: LUFE: The Layman's Unified Field Expose`
~Appendix Set II:~Fundamental Constant ~5. The Atom
Mass variation in the electron by photon absorption, and, The Inverse Square Law. Date first published by itself: 1985-87. Date online: 12-08-08.

Page12p: LUFE: The Layman's Unified Field Expose`
~Acknowledgements and Bibliography~
Date first published by itself: 1985. Date online: 12-08-08.

Page 13: GoMAS: The Geometry of Music, Art and Structure ...linking science, art and esthetics
That simple geometric principles can be responsible for the manifestation of the multitudes of beauty, diversity and richness of Nature is further supported here in this paper. The Inverse-Square-Law (ISL), a simple geometric principle, is shown to be the common link between physics, chemistry, biology, and the science and esthetics of music and art. Nature has incorporated the ISL as the major game rule to building the cosmos. Our perception of pleasing form, color and sound is prophetically built into our sensory being, our biologic evolution, and our structural past. Key to our understanding of the geometry of the ISL is the interference of complementary waveforms. Date first published by itself: 1987, 1996 (updated), and 1998 (condensed). Date online (new, expanded): 03-09-09. New Graphic link added: 10-28-09

Page 14: GoMAC: The Geometry of Music And Color, Parts II and III. How the natural, geometric divisions of the musical monochord and the color spectrum are inherently derived from the same universal law that informs how light, sound, electromagnetism, gravity...indeed, "The Architecture of SpaceTime" itself...behaves. That law is the Inverse Square Law (ISL) and it has a specific relationship to all the quantitative, whole integer numbers as shown in the Brooks (Base) Square matrix (BBS).

Part II of the three-part Geometry of Music And Art (GoMAC) series focuses on a visual journey of how the musical spectrum...and specifically the chromatic and diatonic scales...is based on the ISL.

A visual walk-through and summary of key concepts relating the ISL-derived Brooks (Base) Square, BBS, matrix with a geometrically derived division of both the musical monochord...resulting in the chromatic and diatonic major scale...and the color spectrum (as seen in GoMAC part III). Modulations around the Circle of Fifths and the Golden Rectangle are...key.

Based on "The Geometry of Music, Art and Structure...linking science, art and esthetics" white paper, "Geometry of Music And Color, I" new media net.art project, and the BBS matrix. Original soundtracks (A and B).

Part III focuses on a visual journey of how the color spectrum...and specifically the complementary colors of each hue, is based on the ISL.

A visual walk-through and summary of key concepts relating the ISL-derived Brooks (Base) Square, BBS, matrix with a geometrically derived division of both the musical monochord...resulting in the chromatic and diatonic major scale (part II)...and the color spectrum, in which color complements inside and outside of the 400-750 nm visible spectrum dictate the colors that we perceive.

Based on "The Geometry of Music, Art and Structure...linking science, art and esthetics" white paper, "Geometry of Music And Color, I" new media net.art project, and the BBS matrix. Original soundtracks (C and D).Date on line: 05-25-12

Page 15: Brooks (Base) Square (BS): The Architecture of Space-Time (TAOST) and The Conspicuous Absence of Primes (TCAOP) -the complete work (Rules 1-177)

The table of numbers that, while excluding the *prime numbers ... and only the *prime numbers ... reveals the number patterns that are primary ... primordial ... to the structure of the Universe.

This primordial matrix defines the Inverse Square Law (ISL) that informs gravity, light (electromagnetism) and atomic structure ... the underpinnings of that which we see as the observable Universe.

It is the architecture of space-time itself ... that which ultimately informs ... that is, reveals its disposition that in turn presents the physical laws, and their expression, of light, gravity and the structure of matter ... that fundamentally defines the true structure of the Universe ... seen and unseen ... encompassing all matter (light and dark) and all energy (light and dark).

The ISL is a key relationship describing the interplay of space and time.

It is postulated here that the true underpinnings of space-time itself are inherently defined by numerical relationships ... numbers ... the numbers of Brooks (Base) Square (BS). Date online (Intro) : 12-31-09; Date on line (full version): 05-09-10. Appendix added: 06-01-10. Appendix updated (Rules 178-181) 08-10-10. Appendix B added 11-7-11. Appendix B updated (Rules 182-200) 01-08-12.

Page 16: Brooks (Base) Square interactive (BBSi) matrix: Part I: BASICS
This "BASIC" introduction to the matrix grid and the simplest, most fundamental pattern of the numbers that are formed from the main, Prime Diagonal are presented in a step by step fashion in five different interactive, multimedia formats. The Prime Diagonal is none other than square of the axial numbers (1,2,3,...) forming the core of the Inverse Square Law sequence (1,4, 9,...).

All the numbers...and their many exquisite patterns...are derived directly from the Prime Diagonal numbers. This is Part I. Part II will follow and will present some of the more interesting patterns.

The Inverse Square Law defines how a force or influence (like energy or light) falls off in strength as the distance is increased. It is one of the fundamental relationship laws of the universe effecting everything from gravity to electromagnetism. It can not but help to also be part of the spacetime fabric. It's part of "The Architecture Of SpaceTime" (TAOST). Date online (Intro): 11-05-11. Appendix B added: 11-07-11. Hands-0n Interactive BBS-ISL grids added 10-14-13. Six more instructional MOVIES added 12-18-13.

Page 17: The Architecture Of SpaceTime (TAOST) as defined by the Brooks (Base) Square matrix and the Inverse Square Law (ISL)
"The single most important concept to take from here is that not only is ST not rigid and static...indeed it is more like a fluid made of light, each quanta of which flashes on and off...pulse-propagates into and out of existence...at a frequency (and wavelength) according to its energy...and this fluid light ST unit resonates off a wave of energy at the peak of each pulse-flash...that wave, like a pond ripple, fans out to infinity (or the edge of the Universe...which ever comes first) where it is absorbed back into the sub-Planck event horizon (Singularity) to fuel the next round...communicating...passing on information...as to the location source and energy density...the amount and degree of its presence...its curvature...to every other ST unit throughout the Universe(s), BUT that the ST formation and curvature information propagation is informed, dictated and quantified by the matrix of BBS and the ISL...the bean counters par excellence!" Date online: 12-10-11.

Page 18: Numbers Of Inevitability ~ Let's do a number on that!
Number relationships are like the best and worst...the highest highs, lowest lows...of the most significant human relationships you have ever.... (Read more) Date online: 01-13-12.

Page 19: AFPOP: A Fresh Piece of Pi(e)...and the √2, too...Fractal - Fractal - Fractal
"Circles and squares...as well as other geometric forms...have always been inter-related. Inherent in their geometry is the relationship of their linear elements to their areas...forming the basis of the Inverse Square Law (ISL), as formally presented in the Brooks Base Square (BBS) matrix. At their core, these geometric forms are based on three irrational, infinity-based numbers of proportion...π, √2 and ϕ...pi, the square root of two, and the golden mean. These core proportion-based relationships suggest that they may be acting as fractals in the formation of The Architecture Of SpaceTime (TAOST). Fractals of infinity.!" Date online: 09-01-12.

Pages 20-27: LightspeedST: 0. The Ultimate Question
The Ultimate Question Intro to this 5+-part series examining the fundamental nature of SpaceTime (ST) and the role the constant "the speed of light" plays. Is there a connection? Date online: 03-23-13.

Page 20: LightspeedST: 1. 20 Questions
Part 1 of the 5-part series. Twenty plus question examining the fundamental nature of SpaceTime (ST) and the role the constant "the speed of light" plays. Is there a connection? Date online: 12-13-12.

Page 21: LightspeedST: 2. 20 Answers
Part 2 of the 5-part series. Twenty plus answers to the 20+ questions, framed in bite-sized chunks...the better to swallow and digest these tender new morsels. Lightspeed=ST suggests a new view of our Universe(s). Date online: 12-13-12.

Page 22: LightspeedST: 3. The Mechanics of SpaceTime (ST)
Part 3 of the 5-part series. Actually, this "Portrait of SpaceTime" was written first. (Actually...really...this is all based on L.U.F.E., the Layman's Unified Field Expose´ from 1985. See Links.) The goal: in the most concise and succinct manner...and always with an eye on simplification...lay out the case for tying together the quantum nature of light with the gravitational dependence of spacetime. LightspeedST Parts 1,2,4,and 5 quickly followed as the antidote. Date online: 12-13-12.

Page 23: LightspeedST: 4. The Movie Script
Part 4 of the 5-part series. All text and no play doesn't mean anything more than the notion that every one's individua imagination will play out differently...because that is a good thing! And yet, there is something especially apropos about seeing the original intent...the roadmap to infinity. Don't miss this one! Date text online: 12-13-12. Movies: 02-27-13.

Page 24: LightspeedST: 5. The Movie
Part 5 of the 5-part series. As a visual journey, "LightspeedST: 5. The Movie" will quickly swoosh you...through moving images and text...up and over, down and through, the highlights of LightspeedST...leapfrogging @ the speed of light. Date text online: 12-13-12. Movies: 02-27-13.

Page 25: LightspeedST: 6. Links & References
A quick References and Links page. Date online: 12-13-12.

Page 26: LightspeedST: 7. Quark Portraits
A quick reference to the I- and L-quarks and the composite particles that they make. Includes reference charts, a quick look at L.U.F.E. and The LUFE Matrix, and a whole section on Spinor Rotation. Date online: 01-23-13.

Page 27: LightspeedST: 8. Triad
The triad of velocity, space and time...ruminations. Date online: 03-05-13.

Page 28: LightspeedST: The eBook

This interactive book aims to be useful and valuable to both those who know little about the grand description of our physical world and those who know a lot.

For the new student, let this guide be like a story — really, more like a storyboard — for making a movie about the physical laws of Nature.

You start with the ultimate question: Why is the speed of light constant?

Wow! That's a big question! You break it down to a series of 20 or so smaller questions and answers. How might these go together?

With that preview-overview in mind, you now tell your story with an imaginative mix of words and hundreds of images, with some 50 short videos, all organized around The Players, The Rules, The Subplot, The Plot, and The Conclusion. This is followed up with The Movie (review summary), a substantial Appendix, Links and References, and interactive sketching and note taking widgets embedded throughout.

Without memorizing a single fact, you can experience and gain insight into the workings of Nature.

For the seasoned veteran student immersed in the Standard Model of Quantum Mechanics — matter, fields and exchange quanta; gluons, photons, gravitons, Higgs Bosons, W⁺W⁻Z°; fermions, bosons, leptons, baryons, hadrons; charge, mass and spin vectors; the strong, residual nuclear, weak, electromagnetic and gravitational interactions; the Planck Event Horizon, spinor rotation and much more — and searching to reconcile with General Relativity, this book is exactly what you want to bring fresh insights to that Ultimate Question: Why is the speed of light constant?

This question is so important because it goes directly to the heart of the matter — all matter, all energy — including Dark Matter and Dark Energy.

A unified and harmonious vision of the cosmos awaits you. Date online: 06-05-13.

Page 29: MathspeedST: The eBook

Introducing MathspeedST, an interactive ebook. MathspeedST is the complement to LightspeedST (published in June, 2013).

While LightspeedST addressed the ultimate question: “Why is the speed of light constant?”MathspeedST addresses the fundamental, underlying question: “How can information be ubiquitous, effectively traveling FASTER than the speed of light?”

LightspeedST describes how the formation of spacetime (ST) is intimately tied to the speed of light—all within the Observable Universe.

In the Observable Universe, nothing can travel faster than the speed of light—and this includes any information contained within a tangible form.

In order to satisfy a higher rule, The Conservation of Energy—you know, energy (along with its progeny: momentum, charge, spin, etc.) can neither be net created nor destroyed—clearly a mechanism must be in place to account for the distribution of said energy. Not only that, but such mechanism must do the accounting before—not after—the fact. Enter MathspeedST.

MathspeedST: Leapfrogging Lightspeed FASTER than The Speed of Light” provides the fundamental mathematical basis—lying hidden below—for the accounting and distribution of all spacetime and its subsequent expression as energy, matter and fields in the Observable Universe above.

This freely available interactive ebook brings together under one publication the Brooks (Base) Square-Inverse Square Law, or BBS-ISL matrix for short, under the title MathspeedST. It includes hundreds of images, a number of videos and lots of test-yourself, interactive widgets in presenting the derivation, layout, rules, patterns and ISL-derived mathematical basis of the matrix. Ages 8-10 and up.

A new paradigm in the visualization of basic mathematics is presented!.
Date online: 11-26-13.

Page 30: MathspeedST: The Ubiquitous Information of Numbers (or, How Fractals Exceed the Speed Limit of Light)

The General Ubiquity Rule (GUR) in effect, asserts that if you have a fixed numerical pattern that is ubiquitously present across all space and time (spacetime, ST), that information is present across the same, passing any need to actually travel or transports said information at or above the speed of light.

The Ubiquitous Information of Numbers new media net.art project presents a summary of this idea in a somewhat playful form. The gist of the argument is as stated in the GUR above. A more local example of a checkered tablecloth is used to demonstrate the point. No matter how folded (or not), of whatever size, once you know the pattern of the cloth in any one grid square you know the the pattern of grids at any other spot on the cloth. Substituting the BBS-ISL (Brooks Base Square-Inverse Square Law) matrix, with its fixed numerical pattern that expands across any and all sizes, spaces, and times of distribution, gives us exactly that: The Ubiquitous Information of Numbers.

Based on MathspeedST, an interactive ebook. MathspeedST is the complement to LightspeedST (published in June, 2013).

While LightspeedST addressed the ultimate question: “Why is the speed of light constant?”MathspeedST addresses the fundamental, underlying question: “How can information be ubiquitous, effectively traveling FASTER than the speed of light?”

MathspeedST: Leapfrogging Lightspeed FASTER than The Speed of Light” provides the fundamental mathematical basis—lying hidden below—for the accounting and distribution of all spacetime and its subsequent expression as energy, matter and fields in the Observable Universe above.

This freely available interactive ebook brings together under one publication the Brooks (Base) Square-Inverse Square Law, or BBS-ISL matrix for short, under the title MathspeedST. It includes hundreds of images, a number of videos and lots of test-yourself, interactive widgets in presenting the derivation, layout, rules, patterns and ISL-derived mathematical basis of the matrix. Ages 8-10 and up.

A new paradigm in the visualization of basic mathematics is presented!
Date online: 03-13-14.

A NEW short TPISC: INTRO has been added to ease into this paper!

KEYWORDS TAGS: TPISC, The Pythagorean — Inverse Square Connection, MathspeedST, LightspeedST, BBS-ISL matrix, Brooks (Base) Square, Inverse Square Law (ISL), Pythagorean Triangle, Pythagorean Triple, Pythagorean Primitives, Pythagorean non-primitives, hypotenuse, Dickson Method, Pythagoras Proofs, BASE_3, BASE_5,BASE_4, Teachers, Educators and Students (TES), number theory, ubiquitous informations, FASTER than the speed of light, primes, prime numbers, Pythagorean Theorem,fractals, mathematics, Universe, cosmos, patterns in number.

Art Theory 101 / White Papers Index

PIN: Pattern in Number...from primes to DNA. \| PIN: Butterfly Primes...let the beauty seep in. \| PIN: Butterfly Prime Directive...metamorphosis. \| PIN: Butterfly Prime Determinant Number Array (DNA) ~conspicuous abstinence~. \| GoDNA: the Geometry of DNA (axial view) revealed. \| SCoDNA: the Structure and Chemistry of DNA (axial view). \| The LUFE Matrix \| The LUFE Matrix Supplement \| The LUFE Matrix: Infinite Dimensions \| The LUFE Matrix: E=mc² \| Dark Matter=Dark Energy \| The History of the Universe in Scalar Graphics \| The History of the Universe_update: The Big Void \| Quantum Gravity ...by the book \| The Conservation of SpaceTime \| LUFE: The Layman's Unified Field Expose` \| GoMAS: The Geometry of Music, Art and Structure ...linking science, art and esthetics. Part I \| Brooks (Base) Square (BBS): The Architecture of Space-Time (TAOST) and The Conspicuous Absence of Primes (TCAOP) - a brief introduction to the series

net.art index \| netart01: RealSurReal...aClone, 2001 \| netart02: Hey!Ufunk'n with my DNA? \| netart03: 9-11_remembered \| netart04: Naughty Physics (a.k.a. The LUFE Matrix) \| netart05: Your sFace or Mine? \| netart06: Butterfly Primes \| netart07: Music-Color-ISL \| netart08: BBS-ISL matrix \| netart09: BBS-interactive (I) \| netart10: Sunspots and Solar Flares \| netart11: Music-Color-ISL (II-III) \| Art Theory 101: PIN, DNA, LUFE Matrix, GoMAS, BBS index \| home

Copyright 2014, Reginald Brooks, Brooks Design. All rights reserved.

iTunes, iTunes Store, iBook, iBooks, iBooks Store, iBookstore, iBooks Author, Mac OS are registered® trademarks of Apple Inc. and their use on this webpage does not reflect endorsement by Apple Inc.