Numbers of Inevitability

Let’s do a number on that!

Number relationships are like the best and worst...the highest highs, lowest lows...of the most significant human relationships you have ever known.

When they are really wrong it really shows and pretty much everyone can see it.

And, when they are right...really right...they seem, well, almost inevitable.

Take the squares of any numbers, say, 1, 2, 3, 4, 5, ...

1 squared =1²=  1

2 squared =2²=  4

3 squared =3²=  9

4 squared =4²=16

5 squared =5²=25,...

It’s almost like taking two identical twins and multiplying them together. What do you get? What does 1, 4, 9, 16, 25,... have to do with 1, 2, 3, 4, 5,...? Really?

Isn’t multiplication just a shorthand version of addition?

2²=  4=2+2   yes

3²=  9=3+3   NO

4²=16=4+4   NO

But, wait, think of it a little differently:

Yes, there is this overlap with “2” (Actually, as you purists know, the integers 0, 1, 2 are completely weird in the number universe.).

Is not:Similarly:

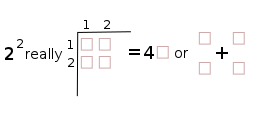
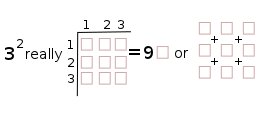
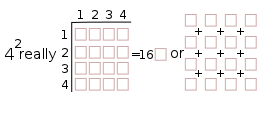
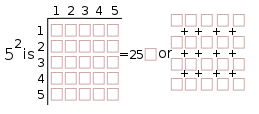
And, now, if we substitute the square (or cube) symbol in the Prime Diagonal with 1, 4, 9, 16, 25,..., we get:

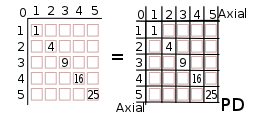
We can graphically see one example of an inevitable relationship of numbers. The squares of the Axial numbers are found on the main (Prime) Diagonal on a multiplication table of the numbers 1, 2, 3, 4, 5, .... This became the initial starting point for the Brooks Base Square (BBS) matrix that reveals...and defines...the Inverse Square Law (ISL).But, things changed...at least for the BBS matrix.

It’s called a matrix (“Mathematics a rectangular array of quantities or expressions in rows and columns that is treated as a single entity and manipulated according to particular rules. “ )...and not a multiplication table...because once the 1, 4, 9, 16, 25, ...squared Axis numbers are plotted on the main (Prime) Diagonal, all the remaining numbers inside the matrix are not derived from multiplying the Axial numbers. The follow a series of rules.

These Inner Grid (IG) numbers are, instead, derived from the Prime Diagonal (PD) numbers...by subtraction! Yes, that’s right, subtraction...or as we all know, addition in reverse gear.

The IG numbers are all derived by subtracting the 1, 4, 9, 16, 25, ...PD numbers from each other! (This was the main pattern revealed in BBSinteractive: BASICS.)

Ok...so what?

Well, these IG numbers are fully numbers of inevitability. They, along with the Axial and PD numbers that together form the infinitely expandable BBS matrix, describe...indeed, inform...much of the Universe. The Universe...the ultimate relationship-based phenomenon...a reiterative, self-similar, holographic-like projection of an underlying, fractal expression of the intimate, inevitable relationship of numbers.

Well, now.... Let’s get on to a simple example as recently presented in the very new APPENDIX B addition to the BBS matrix white paper: EXPONENTIALS.

If the twins of the Axial numbers 1, 2, 3, 4, 5, ...i.e. 1², 2², 3², 4², 5², ...give us the PD numbers, what say of the triples, quadruples, etc.?

This is amazing!

If you take the triples, i.e.  2³, 3³, 4³, 5³,..their product (or sums addition) always is to be found along the 45° diagonal (parallel to the PD) from the Axis number that generated it.

(Note: Since the two IG sections of the BBS matrix are mirror triangular images of each other, it simplifies the view to look at just one of the sections.)

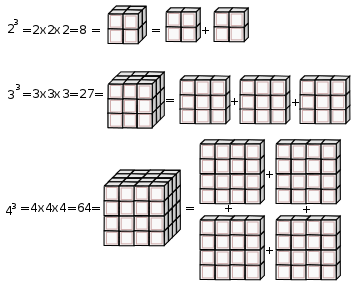
Now here is where it gets really interesting. The 45° diagonal from any Axial number not only contains all the products of any exponential power, i.e. 2³, 2⁴, 2⁵, ..., but the spacing of the steps between successive exponential power products forms a pattern.

This pattern mimics that of the exponential Axial number that formed it. In the example of 2³, 2⁴, 2⁵, 2⁶, 2⁷...this step-spacing pattern grows as 1, 2¹, 2², 2³, 2⁴,... (See Rule 190 in Appendix B.) 

Now, that is truly an example of numbers of inevitability! 

There is much more to come, including:

• Fixed number patterns
• Pythagorean Theorem numbers
• “Penta” 5-based number patterns
• Geometric shapes and their number relationships
• Primes
• Conservation of SpaceTime
• Symmetries
• Operations.

LINKS:

Original BBS matrix & the Inverse Square Law (ISL)

BBSinteractive matrix

Table of Contents

A Brief Introduction

I. TAOST - the network

   A. Geometrics -lines                                       1-50

   B. Geometrics -shapes                                    51-80

   C. Geometrics - relationships

          1. Pythagorean                                       81-99

          2. Parallelogram                                     100-107

          3. Penta                                                108-153

II. TCAOP - everything minus the network

      A. Review of the "Butterfly Primes"

      B. Brooks Square (BS)= the new ISL table matrix

      C. TCAOP=BS-network                                     154

         1. Prime Locator - addition                       155-157

         2. Prime Locator - subtraction                   158-159

         3. Prime Locator - diagonal addition           160         

III. Interconnectedness                   161-175

Conclusion

References

Appendix A                   176-181

Appendix B                   182-200

BBS interactive