Chapter 2C1 - TCAOP - Prime Locator by Addition in Brooks (Base) Square (BS): The Architecture of Space-Time (TAOST) and The Conspicuous Absence of Primes (TCAOP) ~copyright 2010, Reginald Brooks. All rights reserved.

Rules 155-157 will show how the addition of number values from the vertical or diagonal axis to numbers within the Strict Inner Grid result in prime numbers.

~click to enlarge image

155

BS Rule 155: Within the Strict Inner Grid (SIG), there are no prime numbers. However, adding a number from Column A (the vertical axis) to corresponding row number under Column B, D, F, H, J, L, and so on (all from the odd PD numbers), very often results in a prime number. This never happens in Columns C, E, G, I, K, M, and so on (the even PD numbers). In this section, Column Z will refer to the last row number before the PD. They are the numbers in the 1^st diagonal. Plotting the number values in Column A, B and Z, their sums, ∑, and primes, and the differences as one progresses down the column examining each row reveals a strict pattern:

The sums, ∑, of Column A + Z are separated by a difference, ∆, of 3, and the primes located within ... being every other one ... are separated by a ∆ of 6. The sums, ∑, of Column A+B are separated by a difference, ∆, of 6 initially, and thereafter increased by +2 for each row down the column run. The same holds true for the primes.

Note: Column headings for the chart:

Col A: all whole integer numbers
Primes
Out #s: the even numbers “out” of the SIG (not divisible by 4)
PD Out #s: the squares of the primes on the PD (4,9,25,49,...)
In #s: the even numbers “in” the SIG (even #s divisible by 4)
Col Z: the last row number value before the PD
∑ A+Z: the sum of row values from Column A+Z
∆: difference in ∑ values
Primes with ∑: primes found in the ∑ Col A+Z
∆: difference in prime values
Col B: number values from Column B
∑ A+B: the sum of row values from Column A+B
∆: difference in ∑ values
Primes with ∑: primes found in the ∑ Col A+B
∆: difference in prime values

Column A + Z Example
Col A (0,1)	Primes	Out #s	PD Out #s	In #s	Col Z	∑ A+Z	∆	Primes *	∆
2	2				3	5		5
3	3				5	8	3		6
4			4		7	11	3	11
5	5				9	14	3		6
6		6			11	17	3	17
7	7				13	20	3		6
8				8	15	23	3	23
9			9		17	26	3		6
10		10			19	29	3	29
11	11				21	32	3		6
12				12	23	35	3	5x7
13	13				25	38	3		6
14		14			27	41	3	41
15				15	29	44	3		6
16				16	31	47	3	47
17	17				33	50	3		6
18		18			35	53	3	53
19	19				37	56	3		6
20				20	39	59	3	59
21				21	41	62	3		6
22		22			43	65	3	5x13
23	23				45	68	3		6
24				24	47	71	3	71
25			25		49	74	3		6
26		26			51	77	3	7x11
27				27	53	80	3		6
28				28	55	83	3	83
29	29				57	86	3		6
30		30			59	89	3	89
31	31				61	92	3		6
32				32	63	95	3	5x19
33				33	65	98	3		6
34		34			67	101	3	101
35				35	69	104	3		6
36				36	71	107	3	107
37	37				73	110	3		6
38		38			75	113	3	113
39				39	77	116	3		6
40				40	79	119	3	7x17
41	41				81	122	3		6
42		42			83	125	3	5x5x5
43	43				85	128	3		6
44				44	87	131	3	131
45				45	89	134	3		6
46		46			91	137	3	137
47	47				93	140	3		6
48				48	95	143	3	11x13
49			49		97	146	3		6
50		50			99	149	3	149
51				51	101	152	3		6
52				52	103	155	3	5x31
53	53				105	158	3		6
54		54			107	161	3	7x23
55				55	109	164	3		6
56				56	111	167	3	167
57				57	113	170	3		6
58		58			115	173	3	173
59	59				117	176	3		6
60				60	119	179	3	179
61	61				121	182	3		6
62		62			123	185	3	5x37
63				63	125	188	3		6
64				64	127	191	3	191
65				65	129	194	3		6
66		66			131	197	3	197
67	67				133	200	3		6
68				68	135	203	3	7x29
69				69	137	206	3		6
70		70			139	209	3	11x19
71	71				141	212	3		6
72				72	143	215	3	5x43
73	73				145	218	3		6
74		74			147	221	3	13x17
75				75	149	224	3		6
76				76	151	227	3	227
77				77	153	230	3		6
78		78			155	233	3	233
79	79				157	236	3		6
80				80	159	239	3	239
81				81	161	242	3		6
82		82			163	245	3	5x7x7
83	83				165	248	3		6
84				84	167	251	3	251
85				85	169	254	3		6
86		86			171	257	3	257
87				87	173	260	3		6
88				88	175	263	3	263
89	89				177	266	3		6
90		90			179	269	3	269
91				91	181	272	3		6
92				92	183	275	3	5x5x11
93				93	185	278	3		6
94		94			187	281	3	281
95				95	189	284	3		6
96				96	191	287	3	7x41
97	97				193	290	3		6
98		98			195	293	3	293
99				99	197	296	3		6
100				100	199	299	3	13x23
*multiple of two or more primes

Column A + B Example
Col A (0,1)	Primes	Out #s	PD Out #s	In #s	Col B	∑ A+B	∆	Primes	∆
2	2				3	5		5
3	3				8	11	6	11	6
4			4		15	19	8	19	8
5	5				24	29	10	29	10
6		6			35	41	12	41	12
7	7				48	55	14	5x11	14
8				8	63	71	16	71	16
9			9		80	89	18	89	18
10		10			99	109	20	109	20
11	11				120	131	22	131	22
12				12	143	155	24	5x31	24
13	13				168	181	26	181	26
14		14			195	209	28	11x19	28
15				15	224	239	30	239	30
16				16	255	271	32	271	32
17	17				288	305	34	5x61	34
18		18			323	341	36	11x31	36
19	19				360	379	38	379	38
20				20	399	419	40	419	40
21				21	440	461	42	461	42
22		22			483	505	44	5x101	44
23	23				528	551	46	19x29	46
24				24	575	599	48	599	48
25			25		624	649	50	11x59	50
26		26			675	701	52	701	52
27				27	728	755	54	5x151	54
28				28	783	811	56	811	56
29	29				840	869	58	11x79	58
30		30			899	929	60	929	60
31	31				960	991	62	991	62
32				32	1023	1055	64	5x211	64
33				33	1088	1121	66	19x59	66
34		34			1155	1189	68	29x41	68
35				35	1224	1259	70	1259	70
36				36	1295	1331	72	11x121	72
37	37				1368	1405	74	5x281	74
38		38			1443	1481	76	1481	76
39				39	1520	1559	78	1559	78
40				40	1599	1639	80	11x149	80
41	41				1680	1721	82	1721	82
42		42			1763	1805	84	5x361	84
43	43				1848	1891	86	31x61	86
44				44	1935	1979	88	1979	88
45				45	2024	2069	90	5x413	90
*multiple of two or more primes


~click to enlarge image
156	BS Rule 156: The sum, ∑, of the addition of the number values in Column A plus that of each number value in the SIG forms prime #s only under the PD columns with odd #s. All the non-prime odd #s in these ∑ columns are multiples of primes.
Note: Including the numbers of the 1^st Diagonal from the PD ... the numbers 1, 3, 5, 7,... naturally includes primes (underlined) before addition to Column A. The addition of Column A + Z generates additional primes only when the row value under Column A is even or the ∑ of A+Z is divisible by 5 or another prime (e.g. 12+23=35, 22+43=65, 26+51=77, 32+63=95).

[ TOP ]


~click to enlarge image
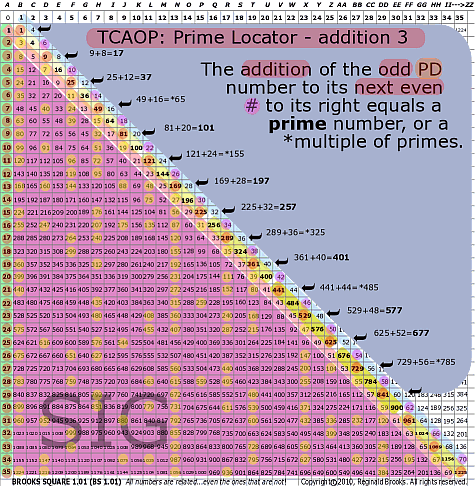
157	BS Rule 157: The addition of the odd PD number to its next even # to its right equals a prime number, or a multiple of primes.

[ TOP ]

Page 2d- PIN: Butterfly Prime Determinant Number Array (DNA) ~conspicuous abstinence~.

Page 7- The LUFE Matrix Supplement: Examples and Proofs: Introduction-Layout & Rules

Page 13- GoMAS: The Geometry of Music, Art and Structure ...linking science, art and esthetics. Part I

Page 14- GoMAS: The Geometry of Music, Art and Structure ...linking science, art and esthetics. Part II

Page 15- Brooks (Base) Square (BS): The Architecture of Space-Time (TAOST) and The Conspicuous Absence of Primes (TCAOP) - a brief introduction to the series

Page 16- Brooks (Base) Square interactive (BBSi) matrix: Part I "BASICS"- a step by step, multi-media interactive

Page 17- The Architecture Of SpaceTime (TAOST) as defined by the Brooks (Base) Square matrix and the Inverse Square Law (ISL).

The LUFE Matrix \| The LUFE Matrix Supplement \| The LUFE Matrix: Infinite Dimensions \| The LUFE Matrix: E=mc² \| Dark Matter=Dark Energy \| The History of the Universe in Scalar Graphics \| The History of the Universe_update: The Big Void \| Quantum Gravity ...by the book \| The Conservation of SpaceTime \| LUFE: The Layman's Unified Field Expose`

net.art index \| netart01: RealSurReal...aClone \| netart02: funk'n DNA/Creation GoDNA \| netart03: 9-11_remembered \| netart04: Naughty Physics (a.k.a. The LUFE Matrix) \| netart05: Your sFace or Mine? \| netart06: Butterfly Primes \| netart07: Geometry of Music Color \| net.games \| Art Theory 101 / White Papers Index