|
| ~click to enlarge image |
|
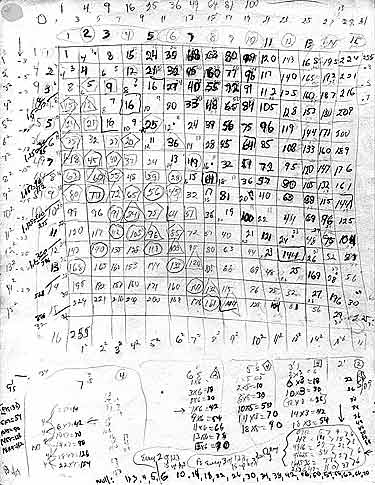
Fig B. The scanned image of the original grid matrix with the inner grid numbers now in place. A number of new relationships involving geometric shapes are shown. |
Brooks (Base) Square (BS) 101
~ The Architecture of Space-Time (TAOST)
&
The Conspicuous Absence of Primes (TCAOP) ~
I. TAOST / A. Geometrics - lines
I. TAOST - the network
A. Geometrics – lines <---
II. TCAOP - everything minus the network
|
TAOST: Rules 1-50 | Rules 51-80 | Rules 81-99 | Rules 100-107 | Rules 108-153 | TCAOP: Rule 154 | Rules 155-157 | Rules 158-159 | Rule 160 | Interconnectedness: Rules 161-175 | Appendix A: Rules 176-181 | Appendix B: Rules 182-200 | |
IA. Geometrics-Basic Lines
In this section, we will be looking at the numerical relationships along the horizontal, vertical and diagonal lines of Brooks Square (BS). In the Brief Introduction, the Base Square (BS) was laid out as two symmetrical triangles joined at the center Prime Diagonal (PD). This is the original, pure form of the new Inverse Square Law (ISL). Table matrix. The matrix which starts out like a typical multiplication table with 0, 1, 2, 3, … along the horizontal and vertical axis and their squares along the PD. There it ends as a typical multiplication table for the numbers in between the axes and PD are anything but the simple product of multiplication of the numbers from the two axes. Here … as in from this point forward … is where the magical mystery tour begins. Here Nature reveals her true harmony of the parts to the whole.
While the Base Square (BS 1.00) remains the pure, unadulterated version of the matrix, Brooks Square (BS 1.01+) was born by breaking one diagonal line of symmetry between the two mirror-identical triangles forming the matrix square. And in doing so, opened up and exposed some of the hidden beauty within the grid. Consequently, Brooks Square (BS 1.01+), my personal version … or variation, if you will … of Nature’s pure Base Square (BS 1.00) has been the working version of the most part throughout this paper. When accounting for all of the whole, non-imaginary integers, the Brooks Square (BS 1.01+) version affords a great advantage. Here, have a look.
Note: In order to keep the “Rules” of the matrix and their corresponding images in sync throughout this series, they will be given the same matching reference numbers. All other images, for example the introductory images below, will be referenced as Fig A, Fig B, Fig C, ….
In the two scanned images, Fig A and Fig B, my first attempts … back in May of 2009 … to reveal new relationships between the axis numbers and their squares on the PD of the “bare bones” skeletal ISL grid.

|
| ~click to enlarge image |
|
Fig B. The scanned image of the original grid matrix with the inner grid numbers now in place. A number of new relationships involving geometric shapes are shown. |
The numbers 1, 3, 5, … are the odd-number summation series numbers that inform the ISL, the intensity of the source varies as 1/r2.
As the distance doubles, the force/influence is diluted (inversely decreased) by one fourth. As the distance is tripled, the decrease is by one ninth. As the distance is quadrupled, the decrease is by one sixteenth, and so on. Let, r=distance as radius from the source:
|
r |
r2 |
1/r2 |
|
1 |
1 |
1/1 |
|
2 |
4 |
1/4 |
|
3 |
9 |
1/9 |
|
4 |
16 |
1/16 |
|
5 |
25 |
1/25 |
The odd-number summation series, 1, 3, 5, … , are the numbers between the distance squared … here as r2. They are the difference, ∆, as:
|
r2 |
∆ |
|
0 1 4 9 16 25 |
>1 >3 >5 >7 >9 |
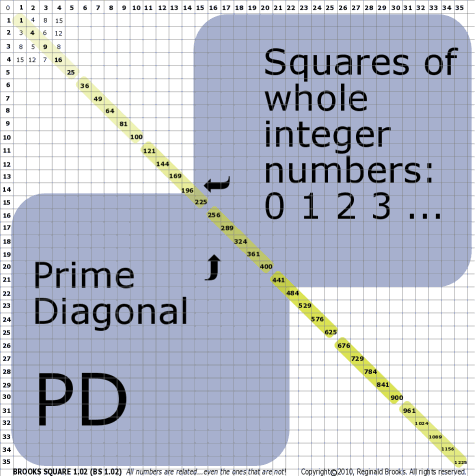
And, when you add them up, they become the numbers of the ISL Prime Diagonal (PD).
0+1=1
1+3=4
4+5=9
9+7=16
16+9=25, and so on, Fig C.
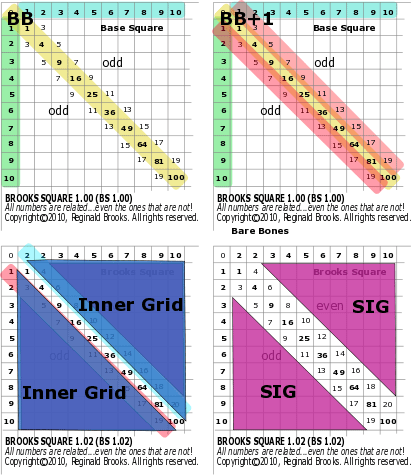
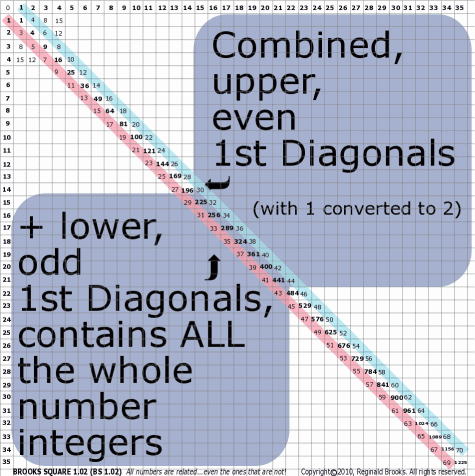
Now for the change in the personal version: On the 1st Diagonal above the PD, the numbers 1, 3, 5, … (from the 1st diagonal below the PD) were changed to their “even” counterparts, 2, 4, 6,… as shown in Fig D.
Enough said, the two versions are the same except for the one simple difference. In most … but not all … cases, the Brooks Square (BS 1.01+) version is used as the example in the rules that follow.
Note: to keep things clear, let’s map out the organization of the grid for future reference. Brooks (Base) Square encompasses both versions of the table matrix: the generic Base and the variation Brooks. The axes + the Prime Diagonal (PD)=Bare Bones (BB). The axes + PD + 1st Diagonals=Bare Bones+1 (BB+1). The grid spots within the BB will simply be called the Inner Grid. When the Inner Grid excludes the 1st Diagonals as well, we will call it the Strict Inner Grid (SIG).
So when we want to refer to the whole matrix square, we will call it just that … the matrix, the grid, the square, Brooks Square, etc.
When we want to refer to only the numbers inside the BB, we will call it the Inner Grid (Grid-BB=Inner Grid).
And, very importantly, when we want to refer to only the numbers inside the BB+1, we will call it the Strict Inner Grid (SIG=Grid-BB+1).
This is a very important distinction because while the grid contains all the numbers, the Strict Inner Grid (SIG) contains NO PRIME NUMBERS (The topic of section II.TCAOP-The Conspicuous Absence of Primes. ).
|
| ~click to enlarge image |
|
Fig E. Brooks (Base) Square grid table matrix reference. A simple reference guide that is useful in mapping out key parts of the square. |
Now, back to the line number relationships within the square.
Ok, now that we have established the number values for the 1st lower diagonal as 1, 3, 5, … (the odd-number summation series), and the 1st upper diagonal as 1, 4, 6, … we can see several relationships right off.
Let’s look at the relationships between the elements of the BB+1 on Brooks Square (BS 1.01+).

|
|
| ~click to enlarge image | |
| 1 | BS Rule 1: Both axis contain all the numbers. |
|
|
| ~click to enlarge image | |
| 2 | BS Rule 2: The Prime Diagonal (PD) contains the square of all the numbers. |
[ TOP ]
|
|
| ~click to enlarge image | |
| 3 | BS Rule 3: Combined, the 1st Diagonals contain all the numbers, except 0 and 2. |

|
|
| ~click to enlarge image | |
| 4 | BS Rule 4: The upper 1st diagonal is simply the same numbers as the lower 1st in Base Square (BS 1.00) converted to their even counterparts in Brooks Square (BS 1.01+). |
[ TOP ]

|
|
| ~click to enlarge image | |
| 5 | BS Rule 5: In both 1st Diagonals, the number 1 is actually on the axis and, therefore, is really an axis number. Zero is the origin. |
[ TOP ]
|
TAOST: Rules 1-50 | Rules 51-80 | Rules 81-99 | Rules 100-107 | Rules 108-153 | TCAOP: Rule 154 | Rules 155-157 | Rules 158-159 | Rule 160 | Interconnectedness: Rules 161-175 | Appendix A: Rules 176-181 | Appendix B: Rules 182-200 | |

|
|
| ~click to enlarge image | |
| 6 | BS Rule 6: The odd-number summation numbers can be acquired by simply adding the two adjacent numbers from the axis. |
Note: 1+2=3, 2+3=5, 3+4=5, …. |
|

|
|
| ~click to enlarge image | |
| 7 | BS Rule 7: The even version of the 1st diagonal (upper) can be acquired by simply adding every 2nd number from the axis. |
Note: 1+3=4, 2+4=6, 3+5=8, … |
|
[ TOP ]

|
|
| ~click to enlarge image | |
| 8 | BS Rule 8: Adding every 3rd axis number gives the odd-number summation series. |
Note: 1+4=5, 2+5=7, 3+6=9, … |
|

|
|
| ~click to enlarge image | |
| 9 | BS Rule 9: Adding every 4th axial number gives the numbers of the upper 1st diagonal. |
[ TOP ]
[ TOP ]
|
TAOST: Rules 1-50 | Rules 51-80 | Rules 81-99 | Rules 100-107 | Rules 108-153 | TCAOP: Rule 154 | Rules 155-157 | Rules 158-159 | Rule 160 | Interconnectedness: Rules 161-175 | Appendix A: Rules 176-181 | Appendix B: Rules 182-200 | |

|
|
| ~click to enlarge image | |
| 11 | BS Rule 11: The difference, ∆, between the numbers of the PD are the odd-number summation numbers in the 1st diagonal (lower). |
Note: 4-1=3, 9-4=5, 16-9=7, … |
|

|
|
| ~click to enlarge image | |
| 12 | BS Rule 12: Adding the 1st number below a PD number gives the next number in the PD sequence. |
Note: This is the inverse corollary of BS Rule 11. |
|
[ TOP ]

|
|
| ~click to enlarge image | |
| 13 | BS Rule 13: Adding the 2nd number below a PD number gives the next 2nd subsequent number in the PD sequence. |

|
|
| ~click to enlarge image | |
| 14 | BS Rule 14: Adding the 3rd number below a PD number gives the next 3rd subsequent number in the PD sequence, and so on.
|
[ TOP ]

|
|||||
| ~click to enlarge image | |||||
| 15 | BS Rule 15: The sum, ∑, of adding every axis number to its next axis number increases by 2. |
||||
|
|||||
[ TOP ]
|
TAOST: Rules 1-50 | Rules 51-80 | Rules 81-99 | Rules 100-107 | Rules 108-153 | TCAOP: Rule 154 | Rules 155-157 | Rules 158-159 | Rule 160 | Interconnectedness: Rules 161-175 | Appendix A: Rules 176-181 | Appendix B: Rules 182-200 | |

|
|||||
| ~click to enlarge image | |||||
| 16 | BS Rule 16: The sum, ∑, of adding every axis number to its 2nd subsequent number increases by 2.
|
||||
|
|||||

|
|||||
| ~click to enlarge image | |||||
| 17 | BS Rule 17: The sum, ∑, of adding every axis number to its 3rd subsequent number increases by 2, and so on. |
||||
|
|||||
[ TOP ]

|
|||||
| ~click to enlarge image | |||||
| 18 | BS Rule 18: The sum, ∑, of adding every 3rd axis number sequentially together increases by 3. |
||||
|
|||||

|
|||||
| ~click to enlarge image | |||||
| 19 | BS Rule 19: The sum, ∑, of adding every 4th axis number sequentially together increases by 4. |
||||
|
|||||
[ TOP ]

|
|||||
| ~click to enlarge image | |||||
| 20 | BS Rule 20: The sum,∑, of adding every 5th axis number sequentially together increases by 5, and so on. |
||||
|
|||||
[ TOP ]
|
TAOST: Rules 1-50 | Rules 51-80 | Rules 81-99 | Rules 100-107 | Rules 108-153 | TCAOP: Rule 154 | Rules 155-157 | Rules 158-159 | Rule 160 | Interconnectedness: Rules 161-175 | Appendix A: Rules 176-181 | Appendix B: Rules 182-200 | |

|
|||||||||
| ~click to enlarge image | |||||||||
| 22 | BS Rule 22: The sum, ∑, of adding every 3rd subsequent 1st diagonal numbers together increases by 6. |
||||||||
|
|||||||||
[ TOP ]

|
|||||||||
| ~click to enlarge image | |||||||||
| 23 | BS Rule 23: The sum, ∑, of adding every 4th subsequent 1st diagonal numbers together increases by 8, and so on. |
||||||||
|
|||||||||
|
|||||||
| ~click to enlarge image | |||||||
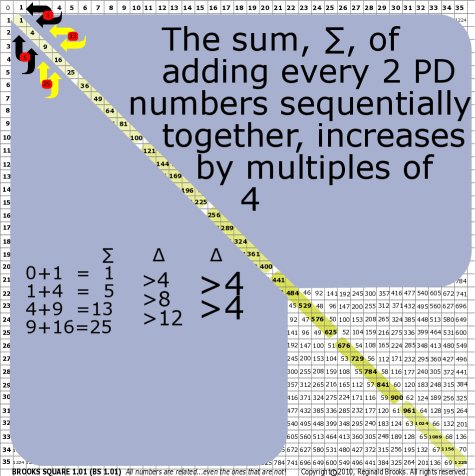
| 24 | BS Rule 24: The sum, ∑, of adding every 2nd PD sequential number together increases by multiples of 4. |
||||||
|
|
|||||||
[ TOP ]
|
|||||||
| ~click to enlarge image | |||||||
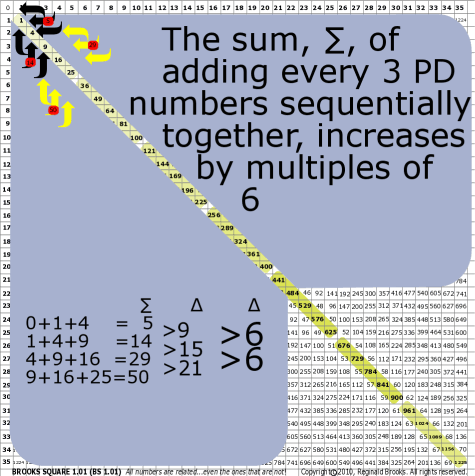
| 25 | BS Rule 25: The sum, ∑, of adding every 3rd PD sequential number together increases by multiples of 6. |
||||||
|
|
|||||||
[ TOP ]
|
TAOST: Rules 1-50 | Rules 51-80 | Rules 81-99 | Rules 100-107 | Rules 108-153 | TCAOP: Rule 154 | Rules 155-157 | Rules 158-159 | Rule 160 | Interconnectedness: Rules 161-175 | Appendix A: Rules 176-181 | Appendix B: Rules 182-200 | |
|
|||||||
| ~click to enlarge image | |||||||
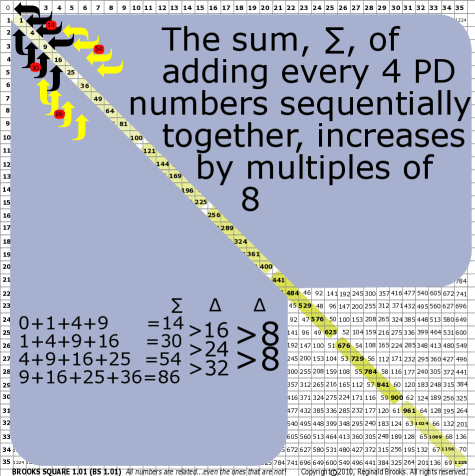
| 26 | BS Rule 26: The sum, ∑, of adding every 4th PD sequential number together increases by multiples of 8, and so on. |
||||||
|
|
|||||||

|
|
| ~click to enlarge image | |
| 27 | BS Rule 27: The PD has a symmetry subset of the 1st number value of each PD diagonal centered around each PD number that is a product of the 5’s (5-based) axis numbers, or multiples of. (see section IC.) |
Note: 1 4 9 16 25 36 49 64 81 100 121 144 169 196 225 256 < ------- ------><----- ---------><--------- -----> |
|
[ TOP ]

|
|
| ~click to enlarge image | |
| 28 | BS Rule 28: The sum, ∑, of the 1st number values between every 5-based PD number is the same, 20. |
Note: 1+4+9+6=20 and, 6+9+4+1=20 |
|

|
|
| ~click to enlarge image | |
| 29 | BS Rule 29: By definition, there are NO PRIME NUMBERS in the PD. |
[ TOP ]

|
|
| ~click to enlarge image | |
| 30 | BS Rule 30: Because the axes and 1st diagonal numbers include ALL the numbers, they of course also include all the prime numbers. |
[ TOP ]
Now that a few trivial number relationships in the Bare Bones + 1st Diagonals (BB+1) have been described, let’s proceed on and into the interior of the matrix. This is where all the really juicy stuff lies … or should we say, hides.
By implementing BS Rules 11-14, we can now complete the grid, Fig F and Fig G.

|
| ~click to enlarge image |
|
Fig F. Brooks Square (BS 1.01+) This is the standard working version of the original Base Square (BS 1.00) with converted 1st diagonal. |

|
| ~click to enlarge image |
|
Fig G. Remembering that the upper and lower triangle of the grid are symmetrically equal (except for the 1st diagonal even modification), comments about the grid apply to both. Typically, the lower triangle will be used to demonstrate the number relationships unless the needs of both are required. |
|
TAOST: Rules 1-50 | Rules 51-80 | Rules 81-99 | Rules 100-107 | Rules 108-153 | TCAOP: Rule 154 | Rules 155-157 | Rules 158-159 | Rule 160 | Interconnectedness: Rules 161-175 | Appendix A: Rules 176-181 | Appendix B: Rules 182-200 | |
|
|
| ~click to enlarge image | |
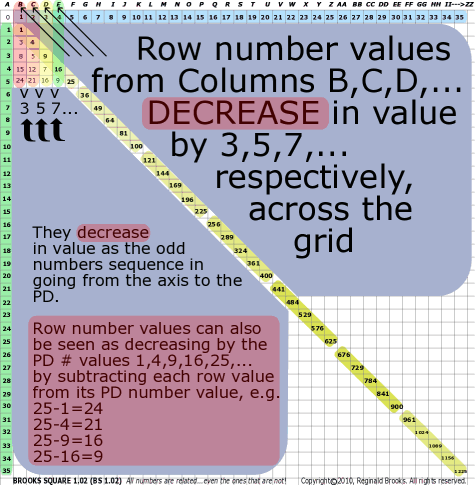
| 31 | BS Rule 31: Row numbers from Columns B, C, D, … decrease in value by 3, 5, 7, …, respectively. |
Note: The row ∆’s are the odd-numbers |
|

|
|
| ~click to enlarge image | |
| 32 | BS Rule 32: Column numbers from Rows 2, 3, 4, … increase by 5, 7, 9, …, respectively. |
Note: The column ∆’s are odd-numbers |
|
[ TOP ]

|
|
| ~click to enlarge image | |
| 33 | BS Rule 33: Diagonal numbers from the 1st, 2nd, 3rd, … diagonal from the PD increase their difference, ∆, in value by 2, 4, 6, …, respectively. |
Note: The diagonal ∆’s are even-numbers. |
|

|
|
| ~click to enlarge image | |
| 34 | BS Rule 34: The difference, ∆, in value of the numbers sequentially in a given 1st, 2nd, 3rd, … diagonal from the PD is simply double the horizontal/vertical axis number that starts that diagonal. |
Note: The ∆ in values follows as 2, 4, 6, …, respectively. |
|
[ TOP ]

|
|
| ~click to enlarge image | |
| 35 | BS Rule 35: Diagonal numbers perpendicular to the PD increase their difference, ∆, in value by 10, 12, 14, …, respectively. |
Note: The diagonal ∆’s are even-numbers. |
|
[ TOP ]
|
TAOST: Rules 1-50 | Rules 51-80 | Rules 81-99 | Rules 100-107 | Rules 108-153 | TCAOP: Rule 154 | Rules 155-157 | Rules 158-159 | Rule 160 | Interconnectedness: Rules 161-175 | Appendix A: Rules 176-181 | Appendix B: Rules 182-200 | |

|
|
| ~click to enlarge image | |
| 36 | BS Rule 36: In perpendicular diagonals, the number closest to the PD (part of the 1, 3, 5, … 1st Diagonal) is ½ the value of the difference, ∆, between the subsequent values in that diagonal sequence. |
| Note: The ∆ in values follows as 5x2, 7x2, 9x2, …, respectively.
|
|

|
|
| ~click to enlarge image | |
| 37 | BS Rule 37: In perpendicular diagonals, the closest number to the PD, starting with the numbers from the 2nd diagonal, is the difference, ∆, in values between subsequent values in that diagonal sequence. |
Note: The ∆ in values follows as 12, 16, 20, …, respectively. |
|
[ TOP ]

|
|
| ~click to enlarge image | |
| 38 | BS Rule 38: Numbers within a diagonal, in either direction, are all odd or all even … never a mixture of both. |

|
|
| ~click to enlarge image | |
| 39 | BS Rule 39: Odd diagonals alternate with even diagonals. |
[ TOP ]

|
|
| ~click to enlarge image | |
| 40 | BS Rule 40: Odd diagonals begin with an odd axis number. |
[ TOP ]
|
TAOST: Rules 1-50 | Rules 51-80 | Rules 81-99 | Rules 100-107 | Rules 108-153 | TCAOP: Rule 154 | Rules 155-157 | Rules 158-159 | Rule 160 | Interconnectedness: Rules 161-175 | Appendix A: Rules 176-181 | Appendix B: Rules 182-200 | |

|
|
| ~click to enlarge image | |
| 41 | BS Rule 41: Even diagonals begin with an even axis number. |
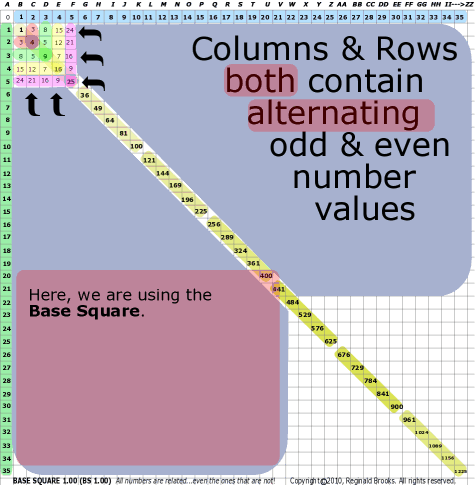
|
|
| ~click to enlarge image | |
| 42 | BS Rule 42: Columns and rows, both, contain alternating odd-even number values. |
[ TOP ]

|
|
| ~click to enlarge image | |
| 43 | BS Rule 43: Odd columns and rows, both, start with even axis number values. |

|
|
| ~click to enlarge image | |
| 44 | BS Rule 44: Even columns and rows, both, start with odd axis number values. |
[ TOP ]

|
|
| ~click to enlarge image | |
| 45 | BS Rule 45: The number of numbers in a given row … including the axis number, excluding the PD number … equals the respective axis number. |
[ TOP ]
|
TAOST: Rules 1-50 | Rules 51-80 | Rules 81-99 | Rules 100-107 | Rules 108-153 | TCAOP: Rule 154 | Rules 155-157 | Rules 158-159 | Rule 160 | Interconnectedness: Rules 161-175 | Appendix A: Rules 176-181 | Appendix B: Rules 182-200 | |

|
|
| ~click to enlarge image | |
| 46 | BS Rule 46: There are NO PRIME NUMBERS in the Strict Inner Grid, SIG. |
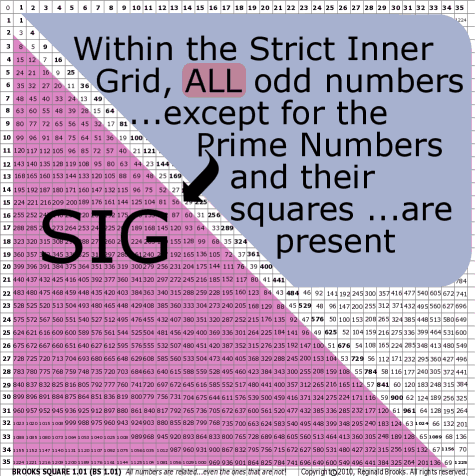
|
|
| ~click to enlarge image | |
| 47 | BS Rule 47: Within the Strict Inner Grid, all odd numbers … except for primes or squares of primes … are present. |
[ TOP ]

|
|
| ~click to enlarge image | |
| 48 | BS Rule 48: Within the Strict Inner Grid (SIG), the even numbers present begin with 8, and include all subsequent even numbers whose value is a multiple of 4, and follows as 8, 12, 16, 20, 24, …. |
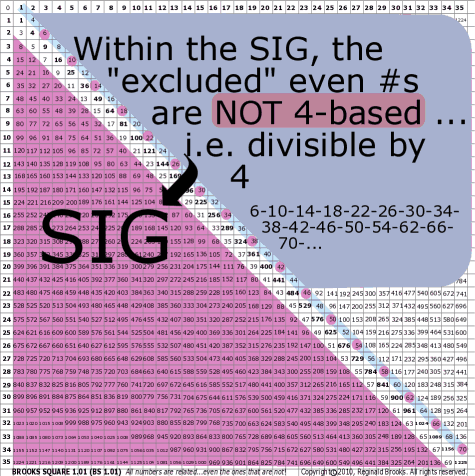
|
|
| ~click to enlarge image | |
| 49 | BS Rule 49: Within the Strict Inner Grid (SIG), the even numbers that are absent are those, starting with 2, whose value is not evenly divisible by 4 … that is, they are the even numbers (past 2), in between the sequence in BS Rule 48 above and when divided by 2 equals the odd-number sequence, as 2, 6, 10, 14, 18, … and divided by 2 equals 1, 3, 5, 7, 9, …. |
[ TOP ]
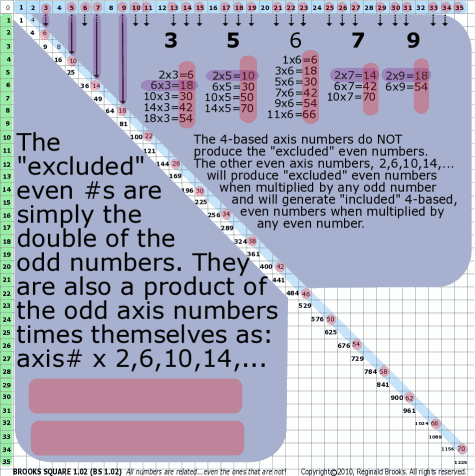
|
|
| ~click to enlarge image | |
| 50 | BS Rule 50: The even numbers absent from the Strict Inner Grid (SIG) are the product of the axis number … except those that are multiples of 4 … times 2, 6, 10, 14, 18, …, respectively. |
[ TOP ]
Each subsequent page in this series will examine new and more dazzling numerical patterns and relationships. So stay onboard, this magical mystery tour is just getting started. Now that the basic lines have been laid out, onto the shapes, and then away we go!
|
TAOST: Rules 1-50 | Rules 51-80 | Rules 81-99 | Rules 100-107 | Rules 108-153 | TCAOP: Rule 154 | Rules 155-157 | Rules 158-159 | Rule 160 | Interconnectedness: Rules 161-175 | Appendix A: Rules 176-181 | Appendix B: Rules 182-200 | |
NEXT: On to
I. TAOST>IB. Geometrics-shapes - Brooks (Base) Square
Back to I. TAOST- the network - Brooks (Base) Square
Page 2a- PIN: Pattern in Number...from primes to DNA.
Page 2b- PIN: Butterfly Primes...let the beauty seep in..
Page 2c- PIN: Butterfly Prime Directive...metamorphosis.
Page 2d- PIN: Butterfly Prime Determinant Number Array (DNA) ~conspicuous abstinence~.
Page 3- GoDNA: the Geometry of DNA (axial view) revealed.
Page 4- SCoDNA: the Structure and Chemistry of DNA (axial view).
Page 5a- Dark-Dark-Light: Dark Matter = Dark Energy
Page 5b- The History of the Universe in Scalar Graphics
Page 5c- The History of the Universe_update: The Big Void
Page 6a- Geometry- Layout
Page 6b- Geometry- Space Or Time Area (SOTA)
Page 6c- Geometry- Space-Time Interactional Dimensions(STID)
Page 6d- Distillation of SI units into ST dimensions
Page 6e- Distillation of SI quantities into ST dimensions
Page 7- The LUFE Matrix Supplement: Examples and Proofs: Introduction-Layout & Rules
Page 7c- The LUFE Matrix Supplement: References
Page 8a- The LUFE Matrix: Infinite Dimensions
Page 9- The LUFE Matrix:E=mc2
Page 10- Quantum Gravity ...by the book
Page 11- Conservation of SpaceTime
Page 12- LUFE: The Layman's Unified Field Expose`
Page 13- GoMAS: The Geometry of Music, Art and Structure ...linking science, art and esthetics. Part I
Page 14- GoMAS: The Geometry of Music, Art and Structure ...linking science, art and esthetics. Part II
Page 15- Brooks (Base) Square (BS): The Architecture of Space-Time (TAOST) and The Conspicuous Absence of Primes (TCAOP) - a brief introduction to the series
Page 16- Brooks (Base) Square interactive (BBSi) matrix: Part I "BASICS"- a step by step, multi-media interactive
Page 17- The Architecture Of SpaceTime (TAOST) as defined by the Brooks (Base) Square matrix and the Inverse Square Law (ISL).
| The LUFE Matrix | The LUFE Matrix Supplement | The LUFE Matrix: Infinite Dimensions | The LUFE Matrix: E=mc2 | Dark Matter=Dark Energy | The History of the Universe in Scalar Graphics | The History of the Universe_update: The Big Void | Quantum Gravity ...by the book | The Conservation of SpaceTime | LUFE: The Layman's Unified Field Expose` | |||||
| net.art index | netart01: RealSurReal...aClone | netart02: funk'n DNA/Creation GoDNA | netart03: 9-11_remembered | netart04: Naughty Physics (a.k.a. The LUFE Matrix) | netart05: Your sFace or Mine? | netart06: Butterfly Primes | netart07: Geometry of Music Color | net.games | Art Theory 101 / White Papers Index | |||||