|
|
| ~click to enlarge image | |
| BP | Fig 3b: A compressed image from "Butterfly Primes" white paper cited above. |
Brooks (Base) Square (BS) 101
~ The Architecture of Space-Time (TAOST)
&
The Conspicuous Absence of Primes (TCAOP) ~
II. TCAOP / A. Review of the “Butterfly Primes”
A Brief Introduction
I. TAOST - the network
II. TCAOP - everything minus the network
A. Review of the "Butterfly Primes" <---
B. Brooks Square (BS)= the new ISL table matrix
2. Prime Locator - subtraction
3. Prime Locator - diagonal addition
|
TAOST: Rules 1-50 | Rules 51-80 | Rules 81-99 | Rules 100-107 | Rules 108-153 | TCAOP: Rule 154 | Rules 155-157 | Rules 158-159 | Rule 160 | Interconnectedness: Rules 161-175 | Appendix A: Rules 176-181 | Appendix B: Rules 182-200 | |
IIA. Review of the “Butterfly Primes”
This is a brief review and reference to earlier work by the author.
Butterfly Primes
~let the beauty seep in~
Copyright© 2005, Reginald Brooks. All rights reserved.
Date completed: 12-07-05
"Introduction
The lure and elusiveness of prime numbers, those very same numbers which all the other natural whole numbers can be reduced to, is thousands of years in the making, captivating the minds of anyone...perhaps everyone...who has ever contemplated their beauty and mystery. Can this beauty reveal a visual and mathematical pattern?
"Given Prime Definition
A prime number ( P ) is any natural whole number ( N ), greater than one, which is reducible only by itself and one.”
“Commentary
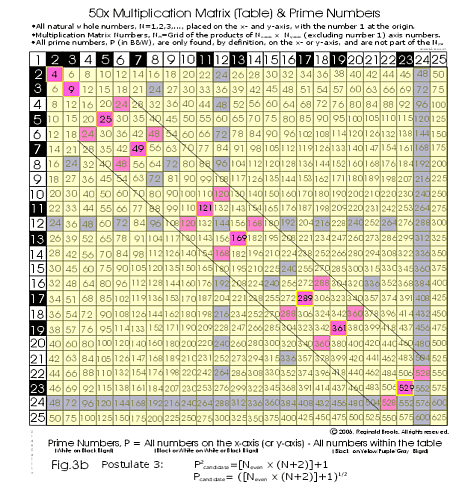
Within the Multiplication Matrix (Table) there are any number of patterns found by delineating the occurrences of a particular number multiple. Here, the concern is with the number 24.
A basic, modular repeating visual pattern is found by highlighting all instances of n24 within the matrix numbers formed from the products of the 1-24 x- and y-axis numbers. This pattern is mirrored in the other three quadrants of an expanded 48 x 48 matrix, and so on...very much a fractal pattern encompassing the products of all numbers.
The original 24 x 24 fractal base pattern is itself composed of four quadrants formed by the crossings of n24s at the product lines of the 12 x- and y-axis. Because the squares of the primes all fall symmetrically on the diagonal drawn from the origin, the focus will be solely on those two quadrants hereafter...though it is to be remembered that the n24 pattern is mirrored in all quadrants as a pattern of eight internal n24s highlights. What remains in this simplification is the "Butterfly Primes" pattern...two diagonally symmetrical quadrant patterns whose eight internal, and 10 axial, n24s highlights radiate out from the center (12 x 12 =144 in this module). This pattern extends diagonally to infinity. In between each and every n24 pair which lies along side the strict diagonal "squares" line (always off the diagonal number by 1), there exists a squared prime number candidate. The pattern is of n24s shepherding the squared primes along the diagonal processional. This pattern defines and predicts all primes when the spurious candidates are eliminated by applying the principles of Postulates 1 and 2.
Twin primes ( P, P+2 ), Prime Triples ( P, P+2, P+6 or P, P+4, P+6 ) and Prime Quadruples ( P, P+2, P+6, P+8 or P, P+2, P+4, P+8 ) and other prime patterns can be seen to result from the logical beauty and order of the "Butterfly" pattern. Fig.3.”
“Conjecture: "Proof of Riemann's Hypothesis"
Taken together, these three postulates prove the order within the prime numbers necessary to establish a non-variance factor (n24)...the landscape at sea level (Riemann's zero points of the zeta function)...the critical line...and it is not "noisy", random or fluctuating, but constant, predictable and straight...and thus proves Riemann's Hypothesis. Each and every prime number square is shepherded along the "squares" diagonal by a series of constant, ordered and symmetrical n24s confirming the larger order of the primes within this "Butterfly" of n24s.”
“New Prime Definition = new "Prime Number Theorem"
A prime number is any natural whole number, greater than one, which is reducible only by itself and one, and, is always separated from the square of all other primes (except P2,3,5 ) by multiplies of 24. The infinity of primes can not exceed the infinity of n24.”
“Conjecture: Primes and the Inverse Square Law
The Inverse Square Law, 1/r2, so fundamental to our physical world...witness gravity and electromagnetism, light and sound, energy, etc...is built on the "odd number summation series", that is, as r, the radius (or distance) increases as 1,2,3,4,5,... the sequential difference between the squares, as r2, follows as 3,5,7,9,11,.... As the distance, r, is doubled, the influence diminishes by 1/4. When r is tripled the influence is reduced by 1/9, when r is quadrupled, the influence drops to 1/16 of the original, and so on. The odd numbers: 1...3...5...7...9... and so on, when added to each other form the sums: 1...4...9...16...25... and so on, forming the "odd number summation series"...the square roots of which form the series: 1,2,3,4,5 and so on.
The "odd number summation series can easily be seen as the diagonal "squares" line on any of the above figures. The odd numbers which form it (when squared), are made of prime and non-prime numbers. The non-prime numbers can be shown to be made of the product of two or more prime numbers. Table IV.
It follows that all odd natural whole numbers, greater than one, are either prime or composed of the product of two or more prime numbers.”
“Conclusion
By using an expanded Multiplication Matrix (Table) and plotting the patterns of the prime numbers on the axis and their squares in the matrix, a strict order based on a factor of 24 was found which is both numerically and visually logical. The difference in squared primes of multiples of 24 allows for the validation of all primes past and the prediction and calculation of all new primes to be easily accomplished. Three Postulates and a new Prime Number Theorem have been offered to summarize and codify these findings...and taken together they define a beautiful ordered pattern within the primes revealing the proof of Riemann's Hypothesis.”
Butterfly Prime Directive
~metamorphosis~
Copyright© 2006, Reginald Brooks. All rights reserved.
Date completed: 01-05-06
“Introduction
This work is based on the "Butterfly Primes...~let the beauty seep in~" (2005), the author's original introduction to the wonderful, butterfly-like pattern of n24s shepherding the prime squares. Three postulates outlined the now formidable characteristics, behavior, predictability and confirmation of all prime numbers.
The conjectures, which naturally follows, is that Riemann's Hypothesis, which ultimately is about proving an ordered pattern for the primes, has been resolved with this work. A new Prime Number Theorem was offered: "A prime number is any natural whole number, greater than one, which is reducible only by itself and one, and, is always separated from the squares of all other primes (except P2,3,5) by multiples of 24. The infinity of primes can not exceed the infinity of n24".
A thorough read of the original paper is a prerequisite to this work.
This paper, "The Prime Number Directive...~metamorphosis~", provides further insight into the foundation of the "Butterfly Primes" pattern and in doing so further substantiates the proof of Riemann's Hypothesis.”
Butterfly Prime Determinate Number Array (DNA)
~conspicuous abstinence~
Copyright© 2006, Reginald Brooks. All rights reserved.
Date completed: 02-15-06
“Introduction
This work is based on the two original papers: "Butterfly Primes...~let the beauty seep in~" (2005), the author's original introduction to the wonderful, butterfly-like pattern of n24s shepherding the prime squares; and, "The Prime Number Directive...~metamorphosis~" (2006), providing further insight into the foundation of the "Butterfly Primes" pattern and the role of the odd non-prime numbers in establishing the primes.
A thorough read of the original two papers is a prerequisite to this work.
In "Butterfly Primes", three postulates and a new Prime Number Theorem were offered to summarize and codify the "Butterfly Primes" pattern. Taken together they define a beautiful ordered pattern within the primes. These postulates were based on a simple multiplication matrix (table).
Postulate 1 essentially defines the primes...and does so by elimination of all the other numbers, which are composites...composed of components other than or in addition to one and themselves.
Postulate 2 revealed the role of multiples of 24 (as n24) as the defining difference in the squares of any and all primes...including the next or any future primes.
Postulate 3, a restatement and refinement of Postulate 2 in visual...as well as mathematical... terms, presented the "Butterfly Primes" pattern as a modular, repeating, fractal-like pattern which both defines and predicts all prime number candidates.
The new Prime Number Theorem proposed: "A prime number is any natural whole number, greater than one, which is reducible only by itself and one, and, is always separated from the squares of all other primes (except P2,3,5) by multiples of 24. The infinity of primes can not exceed the infinity of n24".
"The Butterfly Prime Directive" took a harder look at all the odd numbers as seen through the filter of the n24 lens. The conclusion drawn was that all odd numbers fall into one of three groups:
“Plan
In this paper, a further refinement presents the same information in a new clarifying light. Once again looking at the distinct patterns of the non-primes reveals the primes, and their pattern that emerges, to be that which is left over...a determinate number array. It is like finding a positive space pattern in the odd non-primes, only to reveal in the ensuing negative space so formed...the primes. The challenge is to present the patterns of both the positive and negative space...for one cannot see the one without the other...in clear and precise form!”
“Conclusion
History has shown that often when looking for the trees the forest is not seen, and conversely, when looking for the forest, who knew there were trees. The pattern of the primes, while under the glare of the mathematical lights, has been elusive...yet tantalizingly close at hand. No doubt the primes were given the status of the trees and the other numbers, the rest of the forest, was little more than brush and saplings.
A more visual, less linear, approach to looking at the primes resulted in the "Butterfly Primes" pattern emerging from the common multiplication matrix (table). The pattern was striking, repetitive and largely predictable as formed from multiplies of an even number, 24, and referred to as n24. While giving an undeniably visual and mathematical presentation to the pattern of the primes it still left the motivation of this pattern unanswered. The notion of what is the forest...really?...was nevertheless raised.
The investigation continued. What is the relationship of any and all of the odd numbers to this n24? "The Butterfly Prime Directive" revealed a forest...a true forest...of big and little trees of at least several species, some of which were prime, some were "prime-like" (but not actually prime) and some of which were not prime or "prime-like" in any way. And these were just the trees of odd numbers. What about the trees of even numbers? Gradually, a picture of the forest...the true forest...of numbers began to emerge. The most striking finding was that most of the forest indeed did demonstrate a very strong resonating pattern throughout...but most especially on those trees of odd numbers that are not prime and when these were accounted for (including the even numbered trees), what remained was the prime number trees.
It has been the goal of this paper to focus and sharpen that new vision...that the definite, determinate number array pattern of the primes is formed from and best seen as the reverse pattern of the non-primes. The metaphor was changed. Instead of trees amongst the forest, it has been changed to terminology more appropriate to the technical descriptions of optics, vision and pictorial space...that of positive and negative space. Each defines the other and is equally dependent on the other. By refocusing on all the numbers, a distinct, orderly, repetitive and utterly predictable pattern that becomes the positive form pattern of the odd non-prime numbers emerges...and the reverse, background negative space pattern that remains is that of the primes...a numbered array determined by the pattern of the positive space odd non-primes.”
These papers help place all investigations into the nature of the ISL and Prime Numbers into a larger context. The work that follows does not require any specific familiarity with the above works. They do complement each other. Now onto the current work: Brooks Square.

|
|
| ~click to enlarge image | |
| BP | Fig 3b: A compressed image from "Butterfly Primes" white paper cited above. |
|
TAOST: Rules 1-50 | Rules 51-80 | Rules 81-99 | Rules 100-107 | Rules 108-153 | TCAOP: Rule 154 | Rules 155-157 | Rules 158-159 | Rule 160 | Interconnectedness: Rules 161-175 | Appendix A: Rules 176-181 | Appendix B: Rules 182-200 | |
NEXT: On to
II. TCAOP>IIB. Brooks Square=the new ISL table matrix - Brooks (Base) Square
Back to II. TCAOP - Brooks (Base) Square
Page 2a- PIN: Pattern in Number...from primes to DNA.
Page 2b- PIN: Butterfly Primes...let the beauty seep in..
Page 2c- PIN: Butterfly Prime Directive...metamorphosis.
Page 2d- PIN: Butterfly Prime Determinant Number Array (DNA) ~conspicuous abstinence~.
Page 3- GoDNA: the Geometry of DNA (axial view) revealed.
Page 4- SCoDNA: the Structure and Chemistry of DNA (axial view).
Page 5a- Dark-Dark-Light: Dark Matter = Dark Energy
Page 5b- The History of the Universe in Scalar Graphics
Page 5c- The History of the Universe_update: The Big Void
Page 6a- Geometry- Layout
Page 6b- Geometry- Space Or Time Area (SOTA)
Page 6c- Geometry- Space-Time Interactional Dimensions(STID)
Page 6d- Distillation of SI units into ST dimensions
Page 6e- Distillation of SI quantities into ST dimensions
Page 7- The LUFE Matrix Supplement: Examples and Proofs: Introduction-Layout & Rules
Page 7c- The LUFE Matrix Supplement: References
Page 8a- The LUFE Matrix: Infinite Dimensions
Page 9- The LUFE Matrix:E=mc2
Page 10- Quantum Gravity ...by the book
Page 11- Conservation of SpaceTime
Page 12- LUFE: The Layman's Unified Field Expose`
Page 13- GoMAS: The Geometry of Music, Art and Structure ...linking science, art and esthetics. Part I
Page 14- GoMAS: The Geometry of Music, Art and Structure ...linking science, art and esthetics. Part II
Page 15- Brooks (Base) Square (BS): The Architecture of Space-Time (TAOST) and The Conspicuous Absence of Primes (TCAOP) - a brief introduction to the series
Page 16- Brooks (Base) Square interactive (BBSi) matrix: Part I "BASICS"- a step by step, multi-media interactive
Page 17- The Architecture Of SpaceTime (TAOST) as defined by the Brooks (Base) Square matrix and the Inverse Square Law (ISL).