|
Reginald Brooks Brooks Design www.brooksdesign-ps.net |
Safari browsers may prefer this page---click here
AFPOP:
A Fresh Piece Of Pi(e)
…and the √2, too…
Fractal - Fractal - Fractal
by Reginald Brooks
©2012, Reginald Brooks. All rights reserved.
Abstract
How does taking a fresh look at pi (π)…and the simple geometry surrounding it…help us see how it relates to the Brooks Base Square (BBS) matrix and the Inverse Square Law (ISL)? Infinite fractals?…fractals of infinity?…how do the irrational numbers π and the √2 become the ambassadors of infinity via the concept of the fractal?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~sidebar: You are Nature…you are infinity. Within your infinite symmetry everything is neat and tidy. Nothing is out of place. Nothing is amiss. Trouble is…and since you are all knowing you know this…it’s boring. Excitement comes from the simple act of breaking one of your symmetries. And that’s because havoc quickly follows this break unless you break another symmetry to balance the first. But the new symmetry of two balancing asymmetries amongst the overall symmetry is hardly worth getting out of bed for. The alarm rings. You wake up with a new resolve to break another symmetry…your third, now…and, of course, another balancing symmetry…your fourth. Hum. The next day, and then the day after that, and the day after that…you do the same so that after one week’s worth of your days you’ve got quite a little mix going. It’s getting a little more exciting. And you are getting excited…but hold on…you have to keep a grip on it…your emotions, that is…because all these asymmetries…and the number keeps growing…are forcing you to keep tract. You’re turning into a frick’n accountant. Quantities! Changes in quantities! How the frock are you going to keep track? After all, if too much of your core symmetries become broken and/or disengaged, you will end up like the other deranged infinities, disappearing into the vapor museum…a.k.a. asylum…of unfulfilled promise. So what do you do? Well, you said you’ve become an accountant, so you do what accountants do, you account…you account for things. Well, hell, there are getting to be an awful lot of things…what, with all theses breaks in the symmetries…to account for. And what do you mean “account for,” anyway? Are we talking specifics; like qualities, like the who, what, when, where, how and why? And for each asymmetry? Hey, remember, while you may b formally known as “infinity,” the name itself drives from “infinite simplicity” which got transformed to “infinitely simple” along the way to “infinity,” while your nickname “beautiful” never fails to get your metaphorical blood running whenever you metaphorically hear it from a metaphorical admirer…”hey, beautiful!” Back to reality. Your simple answer is to quantitate all change…all flux. Be it beans, sprouts, spins, energy densities…you will count…and account for…it all. They call it enumeration…assigning a number, as a symbol…to represent the quantity. The quantity is real. The change in quantity is real. The symbol…the number…is in its strict 1-to-1 correspondence to the quantity…equally as real. Others can change the symbol, manipulate the symbol, or even believe and/or lay claims they are responsible for creating the symbol, but underlying it all, at the root of enumerating quantity…the original symbol-quantity abstraction…the number…remains real. It is part of Nature. Wow! The excitement continues…especially now that the recognition of numbers…that had been there all along…is giving you a fantastic power. A little of this, a little of that…and before you know it, the symphony of all your well-calculated symmetry breaks has given birth…birth! Who’s the father?…to a new form…a new, expressive form of you. It’s like a dream. A reoccurring dream. It’s there when you sleep, gone when you awake, there when you sleep, gone when you awake. Pulsing in and out, on and off, there and not there. The rhythm is not only intoxicating…and it’s very alive…it’s also extremely important…for your dreams while asleep are but manifestations of the symmetries/asymmetries that you have allowed…by counting the numbers…while awake. Cool! But within this new field of energy…manifested during the pulse wave of dream sleep…you want more. More, more, more! You know that manipulating the numbers…the quantities…of the symmetry/asymmetry ratio is the way to do it, yet there must be a simple, elegant way to do so such that resonance and harmony of your growing dream-space perfectly reflects the intentions of your wake-space…that includes an all-encompassing, everlasting reference to your core identity…infinity. It dawns on you that ratio…that is, proportion…is what you have been doing all along and taking this idea…specific ratios of proportion…and applying it as a portal control for the emergence of all quantities…numbers…will instill those same ratios of proportion to all the forms…as open fields of energy and/or as condensed, concentrated fields of energy (a.k.a. matter) presented in the dream-space. Thus the idea of the self-similar, re-iterative fractal was born. And while there are certainly a number of these infinite fractals…or fractals of infinity…around, some of the most important are those that would form The Architecture Of SpaceTime (TAOST). The irrational numbers π, √2 and φ (φ), fit the bill…as they are infinity-based, with their decimal endpoints going to infinity, and, as they are fractal ratios of proportion…building the simple, core geometric shapes of the circle, triangle, square, rectangle, pentagon, etc…all manifesting the dictates of structure and growth as embodied in the Inverse Square Law (ISL) as fully elucidated in the Brooks Base Square (BBS) matrix. So let the fun being. As your infinite wake-time omniscient self plays a pulsing, flickering dream-time movie, you have purpose fulfilled…you are creative! And to add to the excitement, to keep the dream-state interesting, you have given the partially sentient products of your creation just enough of the magic to keep them wondering, too! ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ |
I. Introduction
Since the ideal distribution of an influence…as a force or other form of energy…splays out from a point source as an expanding sphere, it is only appropriate that the 3D Surface Area (SA) of a sphere is relatable back to its simple 2D circular shape…the circle. And, as we know, that largest circle of said sphere has an Area (A) equal to exactly one-fourth the SA.
Simple: SA = 4A or A = SA/4.
Furthermore, the area of a circle…or the SA of its sphere…can be completely represented within the square matrix grid of BBS.
Let’s first briefly look at something old that you all know: simple radius (r), diameter (d) or side (s), Circumference (C) or Perimeter (P), height (h), Area (A), Surface Area (SA), and Volume (V), of simple shapes and forms like the circle/sphere and square/cube, and others.
Next, again briefly, we will look at something very old that you may or may not know or remember…but let’s look at it again with a new twist.
Lastly, let’s take a fresh look at π and its natural relationship with itself and the circle, as well as that with the square. “Natural,” that is, as can be expected from such an infamous, irrational and transcendental number as pi (π).
The two irrational numbers…√2 and π…by definition1 are two iterations of the concept of infinity (∞), expressed in numerous forms. The underlying order of such infinite randomness is revealed in the BBS matrix…the ultimate bean counter of the Inverse Square Law (ISL). The golden ratio φ , has been extensively covered in:
“Geometry of Music And Color, II-III”
To keep things really simple, we will always compare back to simple shapes/forms that have the unity of 1 as one of their defining properties.
There really isn’t anything new here…but more than simply being “much ado about nothing” is getting you into the mind set to appreciate the fresher look ahead. Think fractals.2 Infinite fractals!
II. Something Old
Let’s first briefly look at something old that you all know.
Circle/Sphere & Square/Cube
radius (r), side (s), diameter (d), Circumference (C), Perimeter (P)
Circle/Sphere
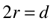
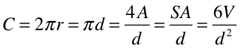
Square/Cube
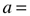 apothem, perpendicular distance from center to side, s
apothem, perpendicular distance from center to side, s
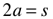
(r=radius, distance from center to vertex)
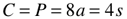
Area (A) and Surface Area (SA)
Circle/Sphere
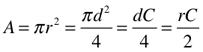
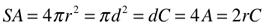
Square/Cube
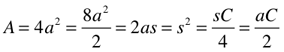
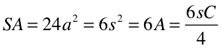
Volume (V)
Circle/Sphere
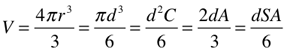
Square/Cube
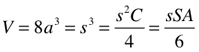
Other Simple Geometric Shapes/Forms
radius (r), apothem (a), side (s), height (h), Perimeter (P)
Equilateral Triangle/Tetrahedron
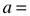 apothem, perpendicular distance from center to side, s
apothem, perpendicular distance from center to side, s
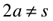
(r=radius, distance from center to vertex)
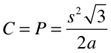
Pentagon
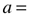 apothem, perpendicular distance from center to side, s
apothem, perpendicular distance from center to side, s
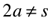
(r=radius, distance from center to vertex)
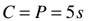
Area (A) and Surface Area (SA)
Equilateral Triangle/Tetrahedron
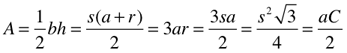
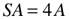
Pentagon
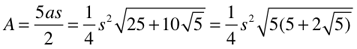
Comparative Charts
Table 1. Comparing Circumference (Perimeter), Area, Surface Area and Volume for the Circle/Sphere, Square/Cube, Equilateral Triangle and the Pentagon based on the diameter (circle) or sides of 1-5 as expressed in π equivalents.
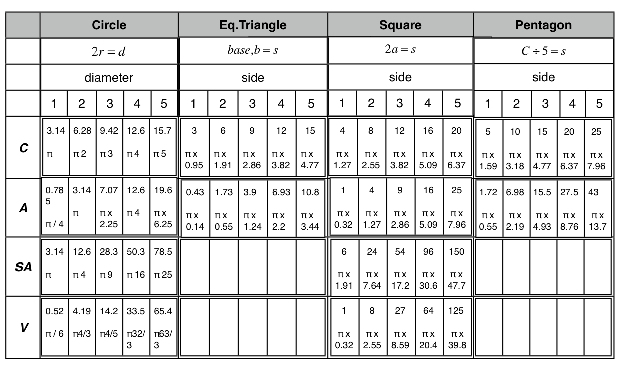
Notice how the Area and Surface Area of the sphere increases as 1, 4, 9, 16, 25 as the radius/diameter grows as 1, 2, 3, 4, 5. As the distance is doubled, which effectively doubles the radius or diameter, the new area of influence…that is, the concentration or density of that influence… is reduced by one quarter as the simple area or surface area exposed increases as the square of that doubling, following the ISL rule of 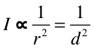 .
.
Table 2. Comparing Circumference (Perimeter), Area, Surface Area and Volume for the Circle/Sphere and Square/Cube based on the diameter (circle) or apothem of 0.5, 1, 2, and 5, as expressed in π equivalents for the circle/sphere or the divisor 4 or 6 for the square/cube.
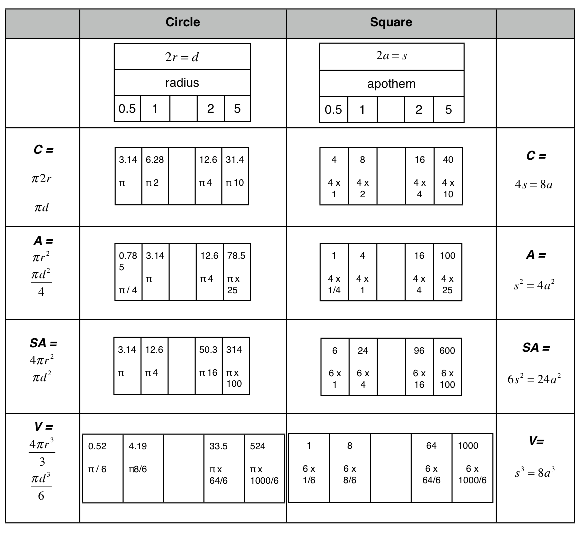
Notice how the Area and Surface Area of the circle/sphere increases as 1, 4, - , 16, -,-,-,-,100 as the radius/diameter grows as 0.5, 1, -, 2,5. As the distance is doubled, which effectively doubles the radius or diameter, the new area of influence…that is, the concentration or density of that influence… is reduced by one quarter as the simple area or surface area exposed increases as the square of that doubling, following the ISL rule of 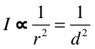 . In the square/cube, this also holds true even as the Surface Area is 6x the square Area versus 4x for the circle. The Volumes work on
. In the square/cube, this also holds true even as the Surface Area is 6x the square Area versus 4x for the circle. The Volumes work on  difference, while the Area and Surface Area follow
difference, while the Area and Surface Area follow  difference.
difference.
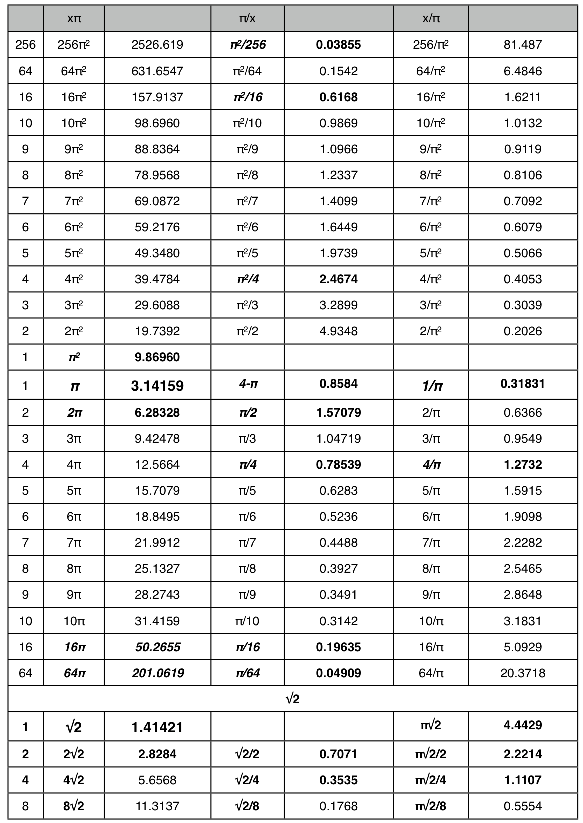
Table 3. Reference Chart for π and √2.
III. Something Really Old…but with a twist
Next, again briefly, we will look at something very old that you may or may not know or remember…but let’s look at it again with a new twist.
Archimedes Proposition #7
Terminology
√2/4 = 0.35355
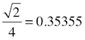
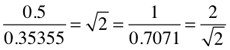
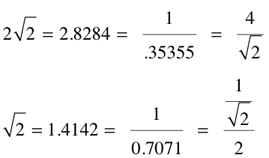
√2/2 = .707107
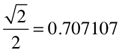
√2 = 1.41421
The square root of two, √2, comes about naturally as a consequence of applying the Pythagorean Theorem to a right-angled triangle with sides equaled to one, 1. The square of the hypotenuse (c) equals the sum of the squares of the sides (a and b).
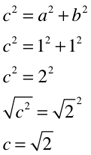
2√2 = 2.8284
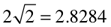
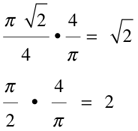
π√2/2 = π/√2 = 2.22144
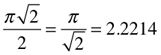
π√2 = 2π/√2 = 4.4429
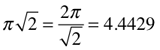
π/2 = π/(√2)2 = 1.5708
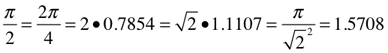
Square Root of Two (√2) Circles & Squares
radius (r), side (s), diameter (d), Circumference (C)
If you circumscribe a circle around a square with sides of 1, the diagonal of that square becomes the hypotenuse of the two triangles that make up said square and they both equal √2. The same √2 diagonal of the square is the √2 diagonal of the circumscribed circle.
Circumscribed Circle/Sphere
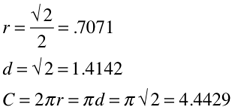
Square/Cube
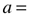 apothem, perpendicular distance from center to side, s
apothem, perpendicular distance from center to side, s
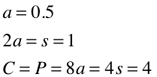
Next, If you inscribe a circle inside the same square above… a square with sides of 1, the diagonal of that new square inscribed inside the new circle becomes the hypotenuse of the two triangles that make up said square and they both equal 1. The same diagonal=1 of the inscribed square is the diagonal=1 of the inscribed circle.
Inscribed Circle/Sphere
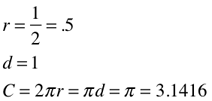
Inscribed Square/Cube
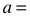 apothem, perpendicular distance from center to side, s
apothem, perpendicular distance from center to side, s
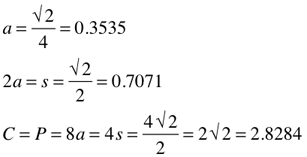
Notice how the 1D parameters of radius, side, diameter and circumference of the larger circumscribed circle are exactly √2=1.4142 times the parameters of the smaller inscribed circle. The same holds true for the two squares, smaller times √2 equals the larger.
Area (A) and Surface Area (SA)
Circumscribed Circle/Sphere
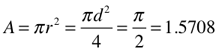
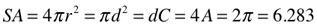
Square/Cube
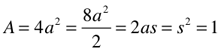
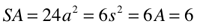
Notice how the 2D parameters of area and surface area of the larger circumscribed circle are exactly 2 times the parameters of the smaller inscribed circle. The same holds true for the two squares, smaller times 2 equals the larger.
Inscribed Circle/Sphere
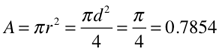
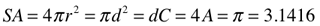
Inscribed Square/Cube
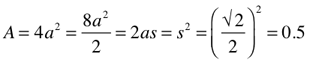
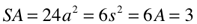
Archimedes is, of course, right…the circumscribed circle around the square has twice the area its inscribed circle.
Interestingly, if the square chosen has unity sides (s=1), the linear parameters of radius, diameter and circumference of the circumscribed circle…and corresponding apothem, side and perimeter of the larger square…are √2 times larger, respectively, of their corresponding inscribed circle…or square. This √2 relationship holds true across all sizes of circles and squares.
IV. Something New
Let’s take a fresh look at π and its natural relationship with itself and the circle, as well as that with the square.
Terminology
§ (~0.8584) = difference (∆) between the Perimeter (P=4) of a square with unity sides (s=1), and, the Circumference (C=π) of a circle drawn with the same diameter (d=1). The Circumference of that circle equals π and a 90° quadrant (arc) is equal to π /4, or ~0.7854. The difference (∆) between this and the square’s quadrant value of 1, equals 0.2146.
§ = 4-π = 0.858407 = 0.85841
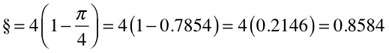
§.25 = §/4 = 0.2146
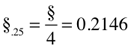
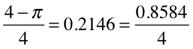
π.25 + §.25 = 0.7854 + 0.2146 =1
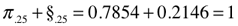
π.25 = π/4 = 0.78539 = 0.7854
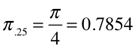
π.25 + §.25 = 0.7854 + 0.2146 =1
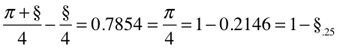
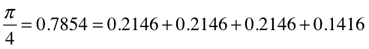
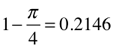
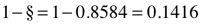
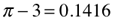
π/2 = 2(π/4) = 1.1107√2 = (π/√2)2/π = 1.5708
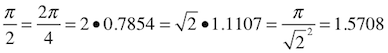
π = 3.14159 = 3.1416
2π = 6.28318 =6.2832
4π =12.566
4/π = 1.2732
π2/46 = 0.0024088 = 0.002409
π2/44 = 0.03855
π2/42 = (π/4)2 = 0.61685
π2= 9.8696 =9.87
42π = 50.265
43π = 201.06
44π = 804.25
π/45 = 0.003068 = 0.00307
π/44= 0.01227
π/43 = 0.04909 = 0.0491
π/42= 0.19634
1-π/4/4 = 0.05365
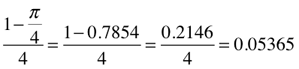
4-π/16 = 0.05365
Parsing The Circle
§ (~0.8584) = the subtractive difference (∆) between the Perimeter (P=4) of a square with unity sides (s=1), and, the Circumference (C=π) of a circle drawn with the same diameter (d=1). The Circumference of that circle equals π and a 90° quadrant (arc) is equal to π /4, or ~0.7854.
Comparing this length of 0.7854 to the length of a quadrant from the Perimeter of the original square, 1.0, reveals that said circle has a Circumference 78.54% (and, 1.0-0.7854=0.2146 and 4 x 0.2146=0.8584) of the square’s Perimeter.
Now…and this is where it gets interesting…if you draw a new square using the 0.7854 length as the side…and thus a 0.3927 apothem (a)…the resulting square has a Perimeter equal to π, and and Area (A) equal to 0.61685, or a ratio ∆ of π/4, or 0.7854, from the original circle Area of 0.7854.
Next, take the side (s=0.7854) of this square and let it be the new Circumference (C=0.7854) of a new circle. The resulting diameter (d=0.25) and radius (r=0.125)…indeed, this also includes the circumference…are all 1/4 that of the original circle, while the Area (A=π/43=0.04909) is 1/16 that of the original circle Area (A=π/4=0.7854). Naturally, a 90° quadrant (arc) of this circle, 0.19635, is also going to now be 1/4 that of its parent circle and square. Notice that ratio ∆ between the circle’s radius (r=0.125) and diameter (d=0.25) and the square’s apothem (a=0.3927) and side (s=0.7854) is π.
Draw a new square using the 0.19635 circle arc length as the side…and thus a 0.09817 apothem…the resulting square has a Perimeter equal to, you guessed it, π/4=0.7854, and Area (A) equal to 0.03855=π2/44, or a ratio ∆ of π/4, or 0.7854, from the previous circle Area (A=0.0.04909). Its apothem, side and Perimeter are all 1/4 it parents values, while its area is 1/16. And so it goes. Each successive circle-square set is related to the previous in an Inverse Square Law (ISL) derivation: as the linear distance is doubled, the area influenced increases by the square of that doubling, i.e., 1/42=1/16. The same as we saw in the previous √2 section. See Tables 4-8.
We have seen how two irrational numbers, π and √2…both numbers which expand to infinity…naturally fit into, indeed generate natural doubling sequences, the ISL and the BBS matrix that reveals it.
We will now sort out the incredible, fractal-like re-iterations of certain π- and √2-based numbers which define this simple beauty of natural forms. But remember, all we are really doing is forming circles and squares 1/2, 1/4, 1/16,…the size of the original unity based forms. So what is the point? The natural way that one size of the form(s) generates the other while perfectly illustrating the Inverse Square Law, and, this dazzling re-iterations of the irrational infinity numbers π and √2 are reason enough.
Table 4. Three circle-square generation sets: Based on π/4=0.7854 90° arc length of the circle’s Circumference (C) becoming the side (s) length of the new square. The second generation (child) set uses the 90° arc length of the parent square’s Perimeter (P) to form the Circumference (C) of the new circle, and so on to the 3rd generation. The initial 1st generation circle was itself based on being inscribed into a unity square.
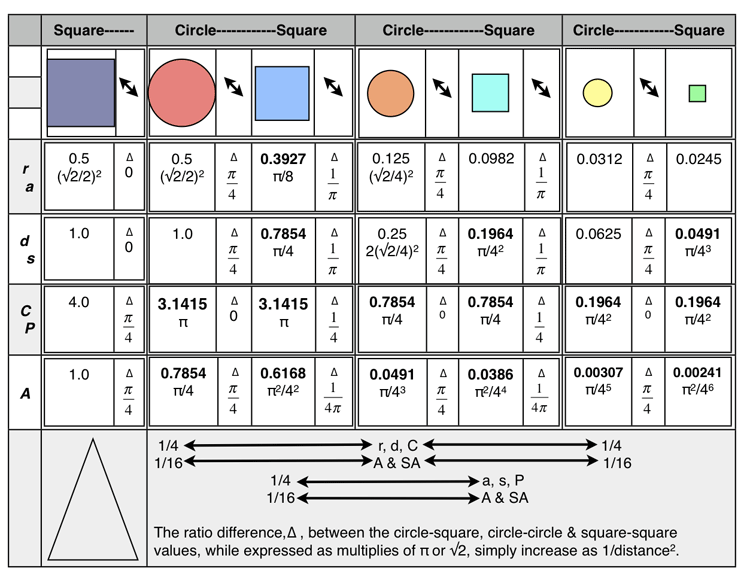
The double arrow columns in the table above reveal the ratio differences, ∆, between the adjacent circle-square generations sets, and, across subsequent generation sets. The larger horizontal row at the bottom summarizes these differences. As the circle/square’s linear values decrease (1/42), their area values fall at a rate that is the square of that linear rate (1/44).
Circle-Circle-Circle or Square-Square-Square
∆ =1/4 x 1/4 = 1/42 = 0.7854/4π = 0.0625
length x 1/42 =new length
∆ = 1/16 x 1/16 = 1/44 = 0.7854/64π = 0.003906
area x 1/44 =new area
Table 5. Three circle-square generation sets: Based on π/4=0.7854 90° arc length of the circle’s Circumference (C) becoming the diameter (d) length of the new circle. The related 1st generation square now using the same Circumference value for its Perimeter (P) length. The second generation (child) set uses the 90° arc length of the parent square’s Perimeter (P) to form the Circumference (C) of the new circle, and so on to the 3rd generation. The initial 1st generation circle was itself based on a unity (d=1) circle…that was inscribed into a unity square as in Table 4.
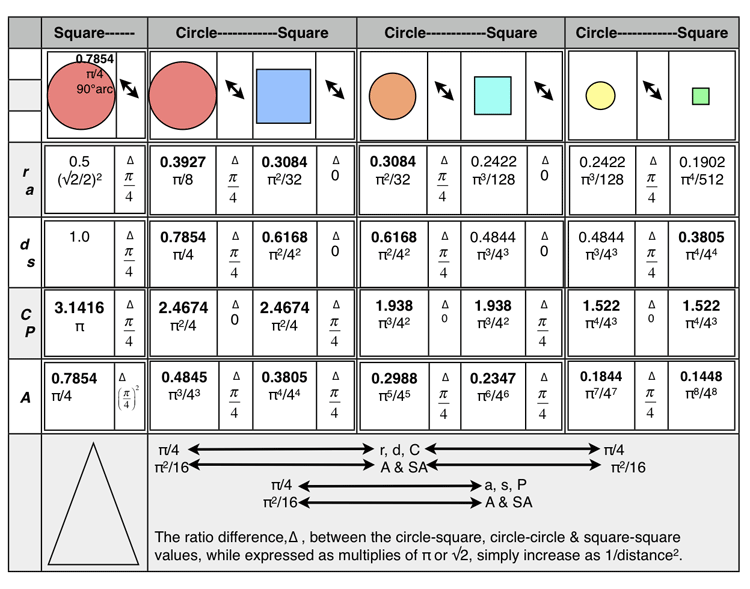
The double arrow columns in the table above reveal the ratio differences, ∆, between the adjacent circle-square generations sets, and, across subsequent generation sets. The larger horizontal row at the bottom summarizes these differences. As the circle/square’s linear values decrease, their area values fall at a rate that is the square of that linear rate.
Circle-Circle-Circle or Square-Square-Square
∆ = π/4 x π/4 = π2/16 = π2/42 = 0.78542 = 0.61685
length x π/42 =new length
∆ = π2/16 x π2/16 = π4/44= 0.78544 = 0.3805
area x π/44 =new area
Table 6. Three circle-square generation sets: Based on √2=1.4142 diagonal length of a unity square becoming the diameter (d) length of the new circle. The related 1st generation square now using the same √2 diagonal value. The second generation (child) set uses the 90° arc length of the parent square’s Perimeter (P) to form the diameter (d) of the new circle and the diagonal of its related 2nd generation square, and so on to the 3rd generation. The initial 1st generation circle was itself based on a unity (s=1) square…the circle was circumscribed over the unity square. Tables 6 and 7 simply validate Archimedes Proposition #7.
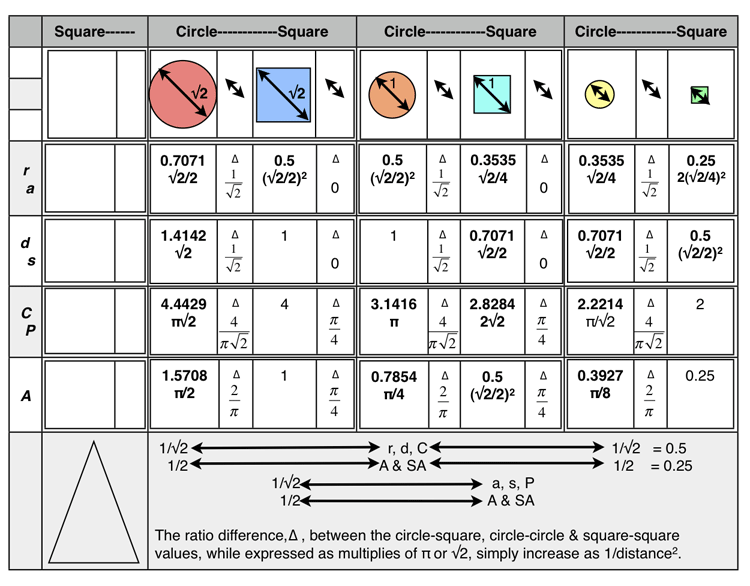
The double arrow columns in the table above reveal the ratio differences, ∆, between the adjacent circle-square generations sets, and, across subsequent generation sets. The larger horizontal row at the bottom summarizes these differences. As the circle/square’s linear values decrease, their area values fall at a rate that is the square of that linear rate.
Circle-Circle-Circle or Square-Square-Square
∆ = 1/√2 x 1/√2 = 1/√22 = 0.70712 = 0.5
length x 1/√22 =new length
∆ = 1/2 x 1/2 = 1/4 = 1/√24 = 0.70714 = 0.25
area x 1/√24 =new area
Table 7. Three circle-square generation sets: Based on 3√2=4.2426 diagonal length of a s=3 square becoming the diameter (d) length of the new circle. The related 1st generation square now using the same 3√2 diagonal value. The second generation (child) set uses the 90° arc length of the parent square’s Perimeter (P) to form the diameter (d) of the new circle and the diagonal of its related 2nd generation square, and so on to the 3rd generation. The initial 1st generation circle was itself based on a (s=1) square…the circle was circumscribed over that square. This whole three generation set was initially formed by randomly selecting a square diagonal number value…in this example the number value of 3 was selected. Tables 6 and 7 simply validate Archimedes Proposition #7.
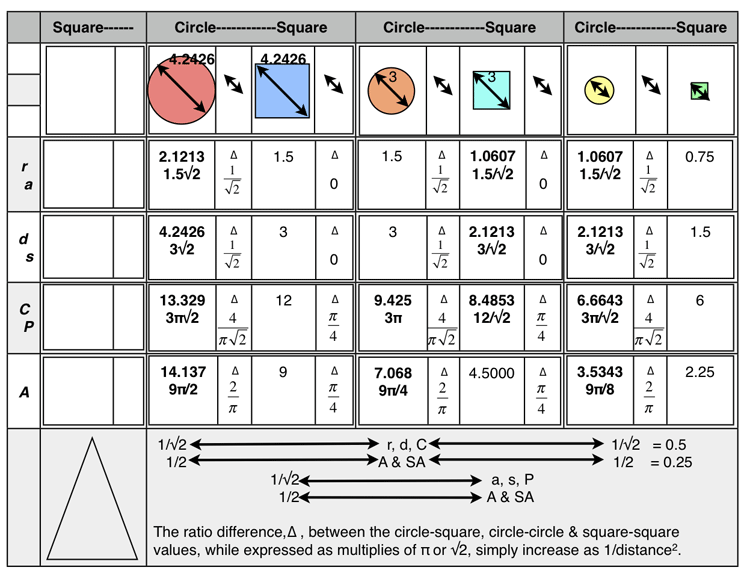
The double arrow columns in the table above reveal the ratio differences, ∆, between the adjacent circle-square generations sets, and, across subsequent generation sets. The larger horizontal row at the bottom summarizes these differences. As the circle/square’s linear values decrease, their area values fall at a rate that is the square of that linear rate.
Circle-Circle-Circle or Square-Square-Square
∆ = 1/√2 x 1/√2 = 1/√22 = 0.70712 = 0.5
length x 1/√22 =new length
∆ = 1/2 x 1/2 = 1/4 = 1/√24 = 0.70714 = 0.25
area x 1/√24 =new area
Table 8. Three circle-square generation sets: Based on π/4=0.7854 90° arc length of the circle’s Circumference (C) becoming the side (s) length of the new square. The second generation (child) set uses the 90° arc length of the parent square’s Perimeter (P) to form the Circumference (C) of the new circle, and so on to the 3rd generation. The initial 1st generation circle was itself based on being inscribed into a unity square. The first half of this table is a repeat of Table 4. Four new rows have been added. We are now going to include the diagonal (dg) value of each circle-square generation set. The first new row is the diagonal value of each respective circle or square, including its expression in terms of π and/or √2, and, the ratio difference, ∆, between them. The next three rows show the diagonal as it is derived from the Area, Circumference/Perimeter, or diameter/side of either its direct parent form above or from the previous form. The latter is done by multiplying the previous form’s Area, Circumference/Perimeter or diameter/side value by the respective ratio difference, ∆, that lies between the two forms listings on the table.
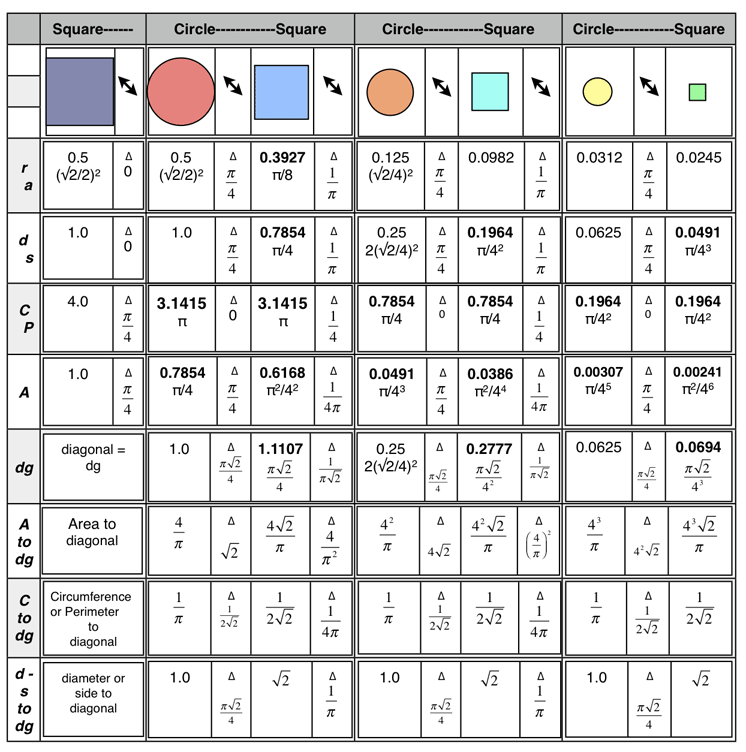
The introduction of the diagonal (dg) value…a geometric description most closely associated with the straight lines of the square-triangle-rectangle (and other straight-sided polygons)… for each of the forms readily brings out the √2 modular, fractal-like behavior in defining these forms and the differences between them.
Side note: Isn’t it interesting how the actual ratio differences can be expressed as simple multiplies of π and/or π/4=0.7854 and √2 and/or √2/2=0.7071, for the π-based Tables 4/5 and the √2-based Tables 6/7, respectively. Yes, that is because those tables were formed by dividing their circles or squares by π- or √2-based parameters, and yet the ultimate simplicity of reducing them to whole number fractions…that is, non-irrational number fractions…is the beauty of it all. Every geometric form…including the simple circle and square…can be simultaneously represented by simple whole integer rational numbers, and at the same time, be completely described by the irrational, infinity bound, fractal numbers π, √2, and their siblings, including  , the golden ratio.
, the golden ratio.
Specifically, the diagonal and diameter of a circle are one and the same, however, the diagonal of a square is not…it being the square root of the sides squared and added.
Whenever the “diagonal” of a circle forms the diagonal of a related square…or vice versa…the ratio difference (∆) between the radius-apothem and diameter-side is always based on √2; the Cirucumference-Perimeter is based on π√2/4; and, the Area on π/2 or π/4, respectively. The √2 is the irrational, fractal that defines the square moment and is true for all sizes.
If instead, the natural, irrational, fractal that defines the circle, π as radius/diameter/Circumference/Area, is used to form a related square…or vice versa…the ratio difference between the radius-apothem, diameter-side, Circumference-Perimeter and Area, will always be based on π, as π, π/4 or 4π, respectively, for all sizes.
In either case, the √2 fractal of the square or the π fractal of the circle, the Area is formed by squaring a length value (and that product multiplied by π for the circle). The ISL is based on this fundamental geometry. Infinities can cancel each other and the irrational can become seemingly rational. Yes Archimedes, that inscribed circle is exactly half that of its related circumscribed parent…as witnessed by the √2.
Figure 1. A Fresh Piece Of Pi(e).
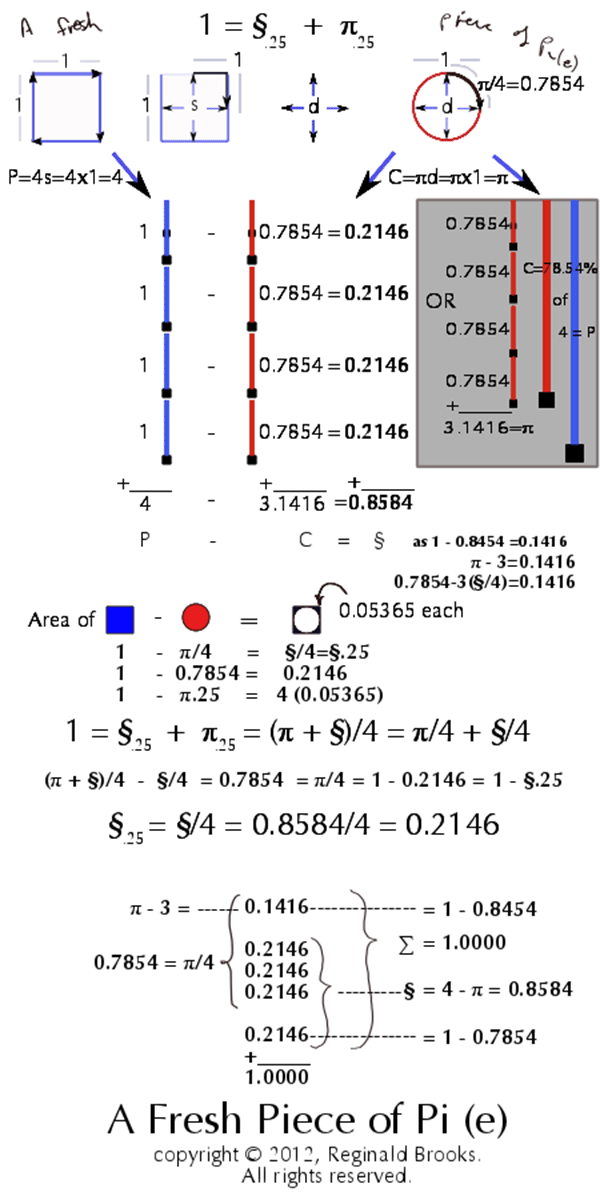
In Figure 1, we have a summary of the thought processes involved in teasing out the simple relationships between a unity square and its related circle. The evolution from these 1st generation sets to subsequent offspring generations came about naturally by using the components of one generation to seed the next. In doing so, not only was simple geometric ratios of the ISL revealed as being inherently built into the very geometric structure of any and all circles and squares…and their 3D sphere and cube counterparts…but also the immense modularity of π, as derived from the circle, and √2, as derived from the diagonal of a unity square, suggests these irrational numbers have the full self-similar, re-iterative identifying characteristics of a fractal. And wouldn’t that make sense. The very fractal-like behavior of the BBS-ISL matrix in its primordial role of informing the architecture of spacetime being itself a distillation of the fundamental circle and square.
Video: Figure 1. “A Fresh Piece of Pi(e)…and the √2, too...Fractal - Fractal - Fractal”
AFPOP: A Fresh Piece of Pi(e) ... and the √2, too ... Fractal - Fractal - Fractal from Reginald Brooks on Vimeo.
Circles and squares...as well as other geometric forms...have always been inter-related. Inherent in their geometry is the relationship of their linear elements to their areas...forming the basis of the Inverse Square Law (ISL), as formally presented in the Brooks Base Square (BBS) matrix. At their core, these geometric forms are based on three irrational, infinity-based numbers of proportion...π, √2 and ϕ...pi, the square root of two, and the golden mean. These core proportion-based relationships suggest that they may be acting as fractals in the formation of The Architecture Of SpaceTime (TAOST). Fractals of infinity.
Copyright 2012, Reginald Brooks. All rights reserved. Links:
white papers:
http://www.brooksdesign-ps.net/Reginald_Brooks/Code/Html/Gomas/gomas09.htm
http://www.brooksdesign-ps.net/Reginald_Brooks/Code/Html/ISL/Brooks_(Base)_Square/BBS-ISLsplashpage.htm
new media net.art projects:
http://www.brooksdesign-ps.net/Reginald_Brooks/Code/Html/netart85.htm
http://www.brooksdesign-ps.net/Reginald_Brooks/Code/Html/ISL/Brooks_(Base)_Square/netart95.htm
artwork:
http://www.brooksdesign-ps.net/Reginald_Brooks/Code/Html/olddraw4.htm
http://www.brooksdesign-ps.net/Reginald_Brooks/Code/Html/newpai11.htm
Thanks for viewing!
V. Commentary
“You can’t get blood out of a turnip” and you can’t get a rational number out of an irrational number…much less a transcendental number like π. What does this mean?
When simple shapes/forms are all definable by irrational numbers like π and √2…and they all are…their exact dimensions can never be determined. And somewhat analogous to the Heisenberg Uncertainty Principle the more accurate your determination of the decimal fraction of π or √2, the less you “know” about its total encompassing properties. The closer you get the further you are from meanfully relating to other parameters. In the end, there is no exact “here.” The circle/sphere, square/cube, etc, are all conceptual forms…not real forms whose start and end points are exactly known.
And yet, here we are! We can count…and counting quantities defines our advanced view toward this conceptual reality. Numbers, as quantities, are just as real as the circles/spheres and squares/cubes that they make. Nature doesn’t need a Phd, college diploma or even a high school GED. Simplicity is at the core.
The question may well be: how does the circle/sphere and square/cube fundamentally relate to each if, indeed, π and √2 are more than simply irrational numbers…that is, numbers whose decimal places run to infinity…but also, and perhaps of equal importance, they are self-similar, re-iterative fractals defining the proportional relationships of the shapes…the architecture…of spacetime itself. This they may well do within the context of the Inverse Square Law (ISL) and the Brooks (Base) Square (BBS) matrix which defines it.
Fundamentally, The Architecture Of SpaceTime (TAOST) must incorporate the BBS-ISL framework because the laws of physics regarding energy, mass, light, sound, etc., describe the complete behavior of their fields as dependent on the ISL.
Together, with the BBS matrix, the BBS-ISL matrix acts as a self-similar, re-iterative fractal…capable of dynamically, and transformatively, generating a full spectrum of ST presentations of every conceivable energy…functionally equivalent to wave properties and their inherent interference effects. Individually examined…as the particle of this duality…we can see and examine the components…numbers…that make up a single fractal array called the BBS-ISL matrix. Built into this, we can also see how π and √2, as fractals themselves, inform the relationships between the parts and the whole of the most basic geometric forms…the circle/sphere and square/cube. In the process, they completely define the basic premise of the ISL.
VI. Conclusion
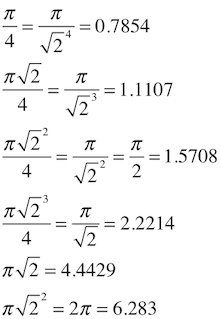
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Infinity must be at least large enough to hold everything…beyond that is anyone’s guess. The irrational numbers, by definition, extend their decimal places to infinity. Linking infinity to formal Euclidean geometric shapes like the triangle, square, pentagon, etc.,…and, of course, the circle…by the irrational, infinity-based fractals…π, √2, and φ …gives resonance and coherence of the one to the other.
Nature, while templating off the Plutonic ideal of perfect Euclidean geometry, in fact manifests her richness and diversity via Riemann non-Euclidean geometric expression…circles are stretched, angles bowed, straight lines curved.
It is the built-in connections of lines and lengths to the areas (and volumes) that form the basis of the ISL that act as fractals, informing the geometry of the distorted, non-Euclidean forms. These rules of embodiment of proportion and relationship are embedded in the BBS-ISL matrix grid…the grid that forms the architecture of spacetime.
As the spacetime geometry is stretched, so too, is the overall BBS-ISL grid, yet on closer exploration, it will be found…like the iconic broken-brushstroke approach of impressionistic/post-impressionistic painting…to be composed of multiples of those pure fractal-based BBS-ISL matrices…whose very fractal Nature is provided by π, √2 and φ.
The Brooks (Base) Square (BBS) matrix that informs and describes the ISL is based on whole integer numbers. Nature enjoys all the numbers; whole, fractional, imaginary, rational and irrational. Nevertheless, the fundamental ISL relationship is inherently built into the simple geometric forms of the circle/sphere and square/cube. Examining such simple forms starting with the simplest unity value of 1 reveals these well known properties. Building up 2nd and 3rd generational sets of circle-squares based on one of the length components of the parent set…that is, based on the radius, apothem, diameter, side, diagonal, circumference, or perimeter…has also revealed the fractal-like behavior of π and √2 in both defining the sibling sets properties, and the ratio differences between the generations, as well. It is no wonder that the BBS-ISL matrix acts like a fractal when building the architecture of spacetime, when, indeed, the generic simple geometric forms that describe the simplest relationship of length, to area, to volume have this very fractal nature built into their geometry.
References
Brooks (Base) Square & The Inverse Square Law (ISL)
http://www.brooksdesign-ps.net/Reginald_Brooks/Code/Html/ISL/Brooks_(Base)_Square/netart95.htm
Brooks (Base) Square (BBS) interactive matrix: BASICS (Part I)
http://www.brooksdesign-ps.net/Reginald_Brooks/Code/Html/ISL/BBS/BBSiI.html
GoDNA: The Geometry of DNA
http://www.brooksdesign-ps.net/Reginald_Brooks/Code/Html/godna2.htm
The Geometry of Music, Art and Structure ...linking science, art and esthetics
http://www.brooksdesign-ps.net/Reginald_Brooks/Code/Html/Gomas/gomas09.htm
Geometry of Music & Color
http://www.brooksdesign-ps.net/Reginald_Brooks/Code/Html/netart85.htm
Geometry of Music And Color, II-III
http://www.brooksdesign-ps.net/Reginald_Brooks/Code/Html/netart12.html
Irrational number
http://en.wikipedia.org/wiki/Irrational_number
Pi (π)
http://en.wikipedia.org/wiki/Pi
√2, Square Root of 2
http://en.wikipedia.org/wiki/Square_root_of_2
√2 and Pythagorean Theorem
http://notaboutapples.wordpress.com/2009/07/20/
the-pythagorean-theorem-and-the-square-root-of-2/
Archimedes' Book of Lemmas
http://en.wikipedia.org/wiki/Book_of_Lemmas
Archimedes of Syracuse
http://en.wikipedia.org/wiki/Archimedes
Pentagon
http://en.wikipedia.org/wiki/Pentagon
http://www.mathopenref.com/polygonsides.html
http://jwilson.coe.uga.edu/EMAT6680/Parsons/MVP6690/Unit/Pentagon/pentagon.html
Fractals
http://en.wikipedia.org/wiki/Fractal
Non-Euclidean Geometry
http://en.wikipedia.org/wiki/Non-Euclidean_geometry
http://en.wikipedia.org/wiki/Fractal
Notes:
1 http://en.wikipedia.org/wiki/Irrational_number
Irrational number
From Wikipedia, the free encyclopedia
Jump to: navigation, search
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number.
Informally, this means that an irrational number cannot be represented as a simple fraction. Irrational numbers are those real numbers that cannot be represented as terminating or repeating decimals. As a consequence of Cantor's proof that the real numbers are uncountable (and the rationals countable) it follows that almost all real numbers are irrational.[1]
When the ratio of lengths of two line segments is irrational, the line segments are also described as being incommensurable, meaning they share no measure in common.
Perhaps the best-known irrational numbers are: the ratio of a circle's circumference to its diameter π, Euler's number e, the golden ratio φ, and the square root of two √2.[2][3][4
2 http://en.wikipedia.org/wiki/Fractal
Fractal
From Wikipedia, the free encyclopedia
A fractal is a mathematical set that has a fractal dimension that usually exceeds its topological dimension[1] and may fall between the integers.[2] Fractals are typically self-similar patterns, where self-similar means they are "the same from near as from far"[3] Fractals may be exactly the same at every scale, or as illustrated in Figure 1, they may be nearly the same at different scales.[2][4][5][6] The definition of fractal goes beyond self-similarity per se to exclude trivial self-similarity and include the idea of a detailed pattern repeating itself.[2]:166; 18[4][7]
As mathematical equations, fractals are usually nowhere differentiable, which means that they cannot be measured in traditional ways.[2][6][8] An infinite fractal curve can be perceived of as winding through space differently from an ordinary line, still being a 1-dimensional line yet having a fractal dimension indicating it also resembles a surface.[1]:48[2]:15
The mathematical roots of the idea of fractals have been traced through a formal path of published works, starting in the 17th century with notions of recursion, then moving through increasingly rigorous mathematical treatment of the concept to the study of continuous but not differentiable functions in the 19th century, and on to the coining of the word fractal in the 20th century with a subsequent burgeoning of interest in fractals and computer-based modelling in the 21st century.[9][10] The term "fractal" was first used by mathematician Benoît Mandelbrot in 1975. Mandelbrot based it on the Latin frāctus meaning "broken" or "fractured", and used it to extend the concept of theoretical fractional dimensions to geometric patterns in nature.[2]:405[7]
There is some disagreement amongst authorities about how the concept of a fractal should be formally defined. The general consensus is that theoretical fractals are infinitely self-similar, iterated, and detailed mathematical constructs having fractal dimensions, of which many examples have been formulated and studied in great depth.[2][4][5] Fractals are not limited to geometric patterns, but can also describe processes in time.[3][6][11] Fractal patterns with various degrees of self-similarity have been rendered or studied in images, structures and sounds[12] and found in nature,[13][14][15][16][17] technology,[18][19][20][21] and art.[22][23][24]
AFPOP: A Fresh Piece of Pi(e)...and the √2, too...Fractal - Fractal - Fractal ©2012, Reginald Brooks, Brooks Design. All rights reserved.