Phi (ϕ), Fibonacci, Pentagon Connections to the PTs

While the LINKS section below the Comments references the historically established connections, the Comments section will address some specific findings — some of them new!

Comments:

The phi (ϕ), Fibonacci and pentagon connections — along with the Kepler Triangle — have some interesting properties that deserve a closer look. Even more so in that they relate back to the DNA double-helix molecule and the geometry of many viruses that transform it.

For reference (2-3 decimals here):

(✓ϕ)² = 1.27

ϕ = 𝞪²/𝛾 = 𝞪𝛾 = 1.618

ϕ² = 𝞪³ = 2.618

𝞪 = ϕ/𝛾 = 1.378 (*fine-structure constant-like approximation, see NOTE)

𝞪² = 𝛾 ϕ = 1.90 ( as 1.8988)

𝞪³ = ϕ² = 2.618

𝞪 ϕ = 2.23

𝞪²ϕ = 3.07

𝛾 = ³✓ϕ = ✓𝞪 = ϕ/𝞪 = 𝞪²/ϕ = 1.174

NOTE:
ϕ = 1.61803 ³√ϕ = 1.174 = 𝛾 𝛾³ = 1.1743 = ϕ 𝞪 = 𝛾² = 1.3782 𝛾= ϕ/𝞪 = 1.61803/1.3782 = 1.1739 These are the original phi (ϕ), 𝞪 and 𝛾 relationships found in the DNA Master Chart. PLEASE NOTE: In all references to the early DNA triangle work, 𝞪 should be correctly designated 𝞪^-1. Back in 2001, the 𝞪 was used as 𝞪 = 1.3782, when in fact it is the reciprocal of 𝞪, as 𝞪 = 1/137, thus 𝞪^-1 is, from this current work on, correctly used as 𝞪 = 0.72…….. The differences in 𝞪-like numbers are shown below this Kepler Triangle-DNA Triangle section in the Tables sections. The correction starts there. This does not preclude the relationships described here, it is only one of proper symbol use. Here 𝞪 = 1.3782, down below in the Tables section, 𝞪 = 0.72…….

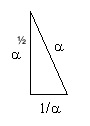
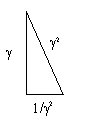
What happens when you square the Kepler Triangle? (square all sides) ;

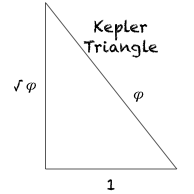
KeplerTriangle

you get

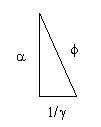
triangle-4

If we set the Kepler Triangle = to the DNA Triangle with hypotenuse=phi (ϕ), it works as we solve for 1.

𝞪² + (1/𝛾)² = ϕ² = 1² + (✓ϕ)²

𝞪² + (1/𝛾)² = 1² + (✓ϕ)²

𝞪² + (1/𝛾)² - (✓ϕ)² = 1² = 1

1.90 + 0.73 - 1.618 = 1

NOTE: The DNA triangles are taken directly from earlier work, NOT scaled here to match the Kepler Triangle.

Another interesting relationship:

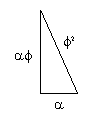
triangle-7

as, ϕ² = 𝞪³ = 2.618

And:

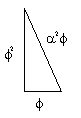
triangle-9

as, ϕ² = 𝞪³ = 2.618

And:

triangle-6

triangle-8

are equal to each other.

*My use of the close approximation to the numbers of alpha, not the actual value, was based on number theory work I was doing back then (2001 and before) on the axial view of the DNA double-helix molecule. I used the 1.3784... number because it kept popping up with my work on phi and the decagons. Something is most definitely there, but my use of it as the fine structure constant per se would probably require a more rigorous proof to be fully accepted as alpha in the physics community. Its approximation to alpha is maintained by the 𝞪 symbol. Key relationships:

ϕ = 𝞪²/𝛾 = 𝞪𝛾 = 1.618
ϕ² = 𝞪³ = 2.618
𝞪 = ϕ/𝛾 = 1.378
𝞪² = 𝛾 ϕ = 1.90 ( as 1.8988)
𝞪³ = ϕ² = 2.618
𝞪 ϕ = 2.23
𝞪²ϕ = 3.07
𝛾 = ³✓ϕ = ✓𝞪 = ϕ/𝞪 = 𝞪²/ϕ = 1.174

As a pure number — 1/1.378 = 0.7255.. — is a fascination that its not to be be ignored! SEE DOWN BELOW!!!

From wikipedia https://en.m.wikipedia.org/wiki/Fine-structure_constant see Feynman quote:

"There is a most profound and beautiful question associated with the observed coupling constant, e – the amplitude for a real electron to emit or absorb a real photon. It is a simple number that has been experimentally determined to be close to 0.08542455. (My physicist friends won't recognize this number, because they like to remember it as the inverse of its square: about 137.03597 with about an uncertainty of about 2 in the last decimal place. It has been a mystery ever since it was discovered more than fifty years ago, and all good theoretical physicists put this number up on their wall and worry about it.) Immediately you would like to know where this number for a coupling comes from: is it related to pi or perhaps to the base of natural logarithms? Nobody knows. It's one of the greatest damn mysteries of physics: a magic number that comes to us with no understanding by man. You might say the "hand of God" wrote that number, and "we don't know how He pushed his pencil." We know what kind of a dance to do experimentally to measure this number very accurately, but we don't know what kind of dance to do on the computer to make this number come out, without putting it in secretly!

— Richard Feynman, Richard P. Feynman (1985). QED: The Strange Theory of Light and Matter. Princeton University Press. p. 129. ISBN 0-691-08388-6."

The above connection of the concentric double-pentagons (decagons) of the axial view of the DNA double-helix molecule to the Kepler Triangle provides yet another connection between phi (ϕ), right triangles and the Pythagorean Theorem, and by inference, the right triangles of the Pythagorean Triples, as they too, have a phi (ϕ) connection via their strong connection with the Fibonacci numbers. The original work, “GoDNA: the Geometry of DNA (axial view),” and, “SCoDNA: Structure & Chemistry of DNA,” generated 3 concentric decagons that were related to each other by phi (ϕ), alpha (𝞪) and the ratio of the two, gamma (𝛾 = ϕ/𝞪). The relationship generated the DNA Master Chart in which every segment of any one decagon relates mathematically to all other segments in the other two. From this a DNA Triangles image was formed:

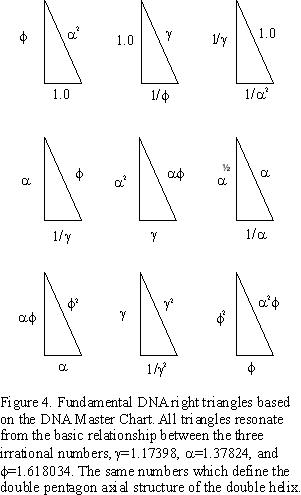
DNAbas42

For more, see the original paper…here.

*The connection between phi (ϕ), the Fibonacci numbers and the BIM (BBS-ISL Matrix) has been extensively covered in the original white paper and ebook "Brooks Base Square and The Inverse Square Law" (2010-11): the specific reference (Rules 161-168) to phi (ϕ), the Fibonacci numbers and the BIM (BBS-ISL Matrix) connection: here

See more of the white papers: here

See more on TPISC: The Pythagorean - Inverse Square Connection: here

 
xxxxxxxxxx

If A = B and B = C, then A = C.

 
xxxxxxxxxx

TABLES I - IV: A deeper look:

Table I. The Fibonacci Numbers are sequentially divided by phi (ϕ) in each Column. Each resolves down to a 𝛾 value in BLUE and a 𝞪 like value in ORANGE. The reciprocal of the 𝞪-like value, 𝞪-1, is shown on the last ROW.

Table II. While the ratios of random, non-Fibonacci numbers added sequentially resolve to phi (ϕ), successive divisions by phi (ϕ) — as shown in each Column — do NOT re-generate themselves, nor do they resolve to 𝞪- or 𝛾-like number values like the Fibonacci does.

Table III. Below, corresponding to three slightly different iterations of √α-1 = 𝛾 as seen in Columns 1,2 — Columns 4,5 — Columns 6,7

Column 1 Reciprocal of 𝞪** -1= 1.3819 as
𝞪** = 0.7236292487 taken from working down Fibonacci Number 89 (Table I)— dividing each Fibonacci number sequentially by ϕ.

Working from the 0.7236292487 on up — multiplying sequentially by ϕ — only works up to 10946 before becoming too large. Col 1,2

Column 4 Reciprocal of the published fine-structure constant = 𝞪**−1** = 137.035999139(31) as α = 0.0072973525664(17).

Working from the 0.72973525664 on up — multiplying sequentially by ϕ — only works up to 55 before becoming too large. Col 4,5 Reference: https://en.wikipedia.org/wiki/Fine-structure_constant

Column 6 Reciprocal of the natural fitting 0.7236067977 = 1/1.3819660113

Working from the 0.7236067977 on up — multiplying sequentially by ϕ — works perfectly at least up to 20,365,011,074. Col 6,7

1.3819660113 × 1.17082 = 1.6180334454 1.170822 = 1.3708194724 1.170823 = 1.6049828547

Here we see that this nearly “perfect” fit 𝞪 = 0.7236067977 = 1/1.38196601 completely re-generates the Fibonacci Numbers Sequence.

As, 𝞪** -1= 1/𝞪 and (1/𝞪)ϕ = ϕ, so 1.3819660113 × 1.17082 = 1.6180334454 and 𝛾2 = 𝞪 -1 , so ** 1.170822 = 1.3708

Less perfect, than the original DNA Triangle values (see above), is 1.170823 = 1.6049828547 — NOT quite ϕ.

~~ ~~ ~~ ~~ ~~

Clearly, these numbers are close — very close — to defining a definitive connection between the Phi (ϕ), the Fibonacci Number Sequence, the pentagon, the Kepler Triangle, the Pythagorean Triples, the DNA double-helix molecule, and perhaps even the fine-structure constant.

Tweaking the values slightly one way satisfies some sets, but not all. Tweaking the values a little the other way satisfies those sets outside, but sacrifices some of the formerly included sets. It may also be simple a matter of scale, i.e. molecular versus atomic.

On the level of physics, and their constants, one would prefer a more definitive connection.

On the level of biology — even though physics informs the chemistry that informs the biology — we can appreciate how the template of the perfect match may enjoy the fruits of diversity by exactly that type of subtle variation from an exact fit!

Table IV. ϕ = 1.61803 3√ϕ = 1.174 = 𝛾 𝛾3 = 1.1743 = ϕ 𝞪 = 𝛾2 = 1.3782 𝛾 = ϕ/𝞪 = 1.61803/1.3782 = 1.1739 The Columns in ORANGE are from the Original DNA Triangle data (𝞪-1 designated as simple 𝞪)

SUMMARY

We have three (3) sets of ϕ—𝞪—𝛾 relationships:

From the original DNA Triangle (as shown in ORANGE in Table IV, Cols. 1-6 ), 𝛾 = 1.1739 or 1.174
From the Fibonacci Number Sequence (Table I, Col. 89; Table III, Col. 1,6; and Table IV, Cols. 7,8 ), 𝛾 = 1.17082 or 1.17086
From the fine-structure constant numbers (Table III, Col. 4), 𝛾 = 1.1807

The latter, somewhat mimicking the actual fine-structure constant, strays the furthest from the others.

No. 1 and 2 are quite close, yet not exactly interchangeable as one plays out the ratios.

The DNA Triangle set is derived from the measurements and calculations of the concentric, double-pentagonal geometry of the axial view (i.e. one complete 360° rotation) of the double-helix spiral. Its tight correlations make for some direct DNA Triangle correlations and a self-consistent DNA Master Chart relating the various geometric segments of the concentric decagons to each other.

The Fibonacci set is taken strictly from calculations: dividing the known Fibonacci Numbers by ϕ. The difference comes from where you start in the sequence and what direction do you go. We know the ratio more perfectly registers the ϕ value, the further along the sequence one goes.

The common factors here are ϕ, the pentagon, and the Fibonacci numbers…and, now perhaps, some common binding factor that has been referred to as gamma, 𝛾.

The Fibonnaci numbers can generate the Pythagorean Triples, and, because of their relationship to ϕ, they are related to pentagons — especially in the form of concentric, double-pentagons.

 
xxxxxxxxxx

Review of the Pythagorean Triples from Wikipedia: here

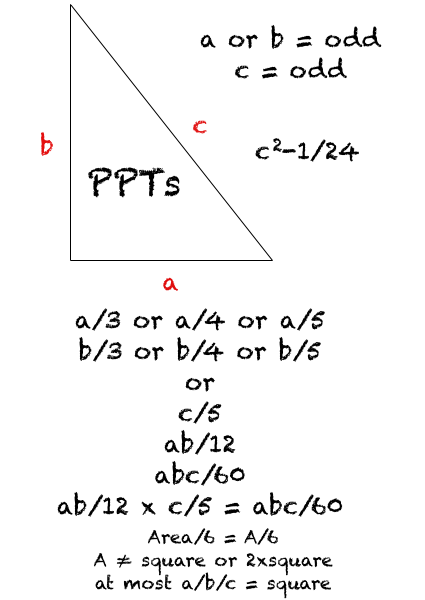
PPTs_basics

Return to the BIM + PT + Pentagons page: here

LINKS:

While there are many excellent reference links available online, the GoldenNumber.net is a great starting point for organization, clarity and thoroughness:

https://www.goldennumber.net

https://www.goldennumber.net/site-map/

https://www.goldennumber.net/geometry/

https://www.goldennumber.net/triangles/

https://www.goldennumber.net/five-phi/

https://www.goldennumber.net/math/

https://www.goldennumber.net/fibonacci-series/

https://www.goldennumber.net/fibonacci-24-pattern/

https://www.goldennumber.net/phi-pi-great-pyramid-egypt/

Another great site covering Numbers (and much more) for education:

http://schoolbag.info/mathematics/numbers/index.html Numbers: Index

http://schoolbag.info/mathematics/numbers/76.html Pythagorean Triples