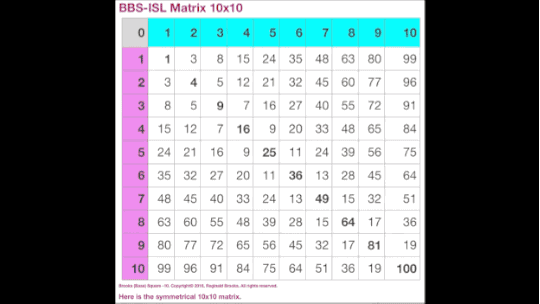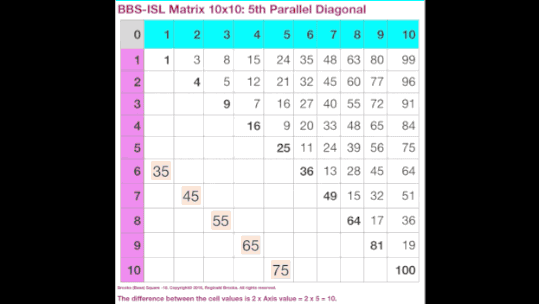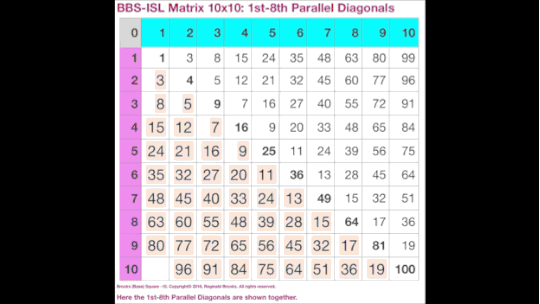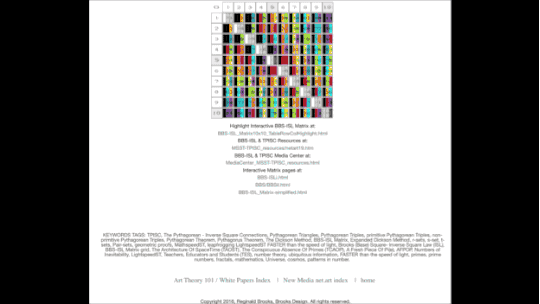
MAP (Math-Art-Physics) IntroThe 1,2,3 of the ISL-PT-PRIMESHere is a very brief highlight of the Inverse Square Law - based grid called the BBS-ISL Matrix (BIM). If you can add - subtract, multiply - divide, you got it. And there are only whole numbers — no fractions. On this grid, we will also briefly highlight the Pythagorean Triples (90° right triangles) and the PRIMES. Again, only whole numbers. There is nothing inherently complicated as we are simply changing the quantities that the numbers represent as we move around the grid. We will break it down to three parts.PART I: making the BIM gridFirst. we all know addition and subtraction are just two sides of the same coin. Differences (∆) are had by giving or taking away some number of quantity.And multiplication is nothing more than a more efficient means of adding. Division is its symmetrical counterpart.And for those jumping ahead, exponentials are just a more efficient means of multiplication, with the root — commonly, the square root — its symmetrical counterpart.Secondly, the BIM grid has its Axis number of 0,1,2,3,.. along its top-bottom and left-right sides. A diagonal running from the top-left corner down is simply the square (multiplication of itself) of the Axis values. It’s called the Prime Diagonal (PD) and it divides the whole BIM grid into two bilaterally symmetric (mirror-image) triangular halves. No, the rest of the matrix grid is not a multiplication table. It is simpler than that: it is filled out by subtracting the vertical PD number (#) from the horizontal PD #, i.e. PD horizontal - PD vertical. These PD #s are taken from where a straight line from any given grid # vertically and horizontally intercepts the PD. Every single Inner Grid # is obtained this way.There are a number of other ways the grid #s can be found. Another really easy one is by addition. The #s of the 1st Parallel Diagonal to the PD is found by adding 2 to the previous #, e.i. 2+3=5, 2+5=7, 2+7=9,…The 2nd Parallel Diagonal is found by adding 4 to the previous #, e.i. 4+8=12, 4+12=16, 4=16=20,…The 3rd Parallel Diagonal is found by adding 6 to the previous #, e.i. 6+15=21, 6+21=27, 6+27=35,… The pattern continues: for each subsequent Parallel Diagonal, 8,10, 12,… (a multiple of 2) is added to the beginning number of the Parallel Diagonal sequence. The first # in the sequence is the PD -1 on that Row.Now you can make the entire BIM grid from a simple 2x2 up to 25x25 to 100,000x100,000 to infinity!PART II: finding the Pythagorean TriplesAs the Pythagorean Theorem is all about showing how the sum of the squares of the two shorter sides of any 90°right-triangle always equal the square of the longer side (a2 + b2 = c2 ), we know that squared numbers are the key. Well, on the BIM, the first squared numbers are on the PD.So just grab one, any one, and follow a straight line down the grid until you intercept another squared number. Bingo! You have just discovered a Row on the BIM that contains a Pythagorean Triple. Look across the Row and you will find the other squared short side, with the squared long side (hypotenuse) at the end of that Row where it intercepts the PD horizontally, e.i. from 9 on the PD, drop down to intercept grid 16 on Row 4, find the other squared short side number , 9, on the Row, and the squared hypotenuse, 25, on the PD at the end of the Row (32 + 42 = 52 ). It’s just that simple. Every Pythagorean Triple (PT) can be found this way!Something interesting happens when you divide all the Inner Grid cells by 24. It selectively underlines the Rows that all Pythagorean Triples might land on. No exceptions. In other words, any squared # on the Inner Grid will always be one of the squared short sides and will always be located on a BIM/24 Row!Part III: finding the hidden PRIMESNow here is where it gets really interesting. While there are no PRIMES on the Strict Inner Grid (Inner Grid minus the 1st Parallel Diagonal of all ODD numbers), every PRIME when joined as a symmetric-pair set of PRIMES will always fall on those same BIM/24 Rows, with one caveat. The BIM/24 Rows may have both a PT and PRIME, neither or one but not the other. The BIM/24 Rows marks the potential location of a PT and/or PRIME but does not guarantee their presence.The PRIMES Sequence (PS) (2),3,5,7,11,13,17,19,23,29,.. when you ignore the #2, will act like a fractal when joined — concatenated — with another PS, generating a Periodic Table Of PRIMES (PTOP). The essence of this table is that pair-sets of 2 PRIMES whose sums equal EVEN #s are formed (PPsets). Turns out one can then transfer this PPset info back onto the original BIM/24, and in doing so we find that each and every one of these fractal-derived PPsets lands exclusively on a BIM/24 Row! And, when the number of said PPsets are treated as Object Areas, these areas are distributed throughout the BIM in a 3,5,7,11,13,17,19,23,29,…PS pattern!And finally, on our brief tour, it must be emphasized that each member of a PPset that is forming an EVEN # lies a symmetrical distance (equally before and equally after) any given EVEN # as located on the BIM Axis (actually on the Axis the EVEN is EVEN/2). That’s right, those patternless PRIMES when grouped in pair-sets demonstrate both a fractal and symmetric pattern heretofore unknown! And as this relationship holds true for every EVEN # on this infinitely expandable BIM grid, Euler’s Strong Form of the Goldbach Conjecture is effectively given proof to be universally true.ConclusionWhile the possible interpretations of how these number dynamics play out in the Cosmos is left for discussion in DSEQEC & CaCoST (Double-Slit Experiment—Quantum Entanglement Conjecture & Creation and Conservation of SpaceTime), it is worth noting that Nature seldom joins three apparently disparate systems as some sort of coincidental lark. Rather, a deep and profound connection between how energy-force dissipates with distance relates to the fundamental relationship between the sides (and areas) of right triangles is perhaps tied together by the fractal, symmetry-driven PRIMES when considered as pair-sets is staring us in the face. Let’s not blink.